弹载小卫星应急发射入轨方法设计与优化*

马特,刘刚,何兵

(火箭军工程大学 空间工程系,陕西 西安 710025)

0 引言

现代小卫星发源于20世纪80年代，是通信技术、测控技术、遥测技术以及小卫星的管理等相关关键技术大力发展的基础上涌现的产物。现代小卫星采用创新概念设计，在大型卫星涉及领域广、技术复杂、研制周期较长、成本过高的背景下，小卫星因其“新、快、灵、省”的特点以及其巨大的发展潜能，出现井喷的态势。随着小卫星的蓬勃发展和广泛应用，小卫星的各项关键技术已经成为航天装备和空间应用领域关键技术的重要组成部分，其中小卫星发射技术则引起各个国家的广泛关注。

小卫星发射方法可以分别为两大类[1]。一是采用专用小型运载火箭发射；二是利用大型运载火箭搭载发射。后者发射周期长，发射点固定，不利于实现需要机动灵活的应急发射任务。而利用现有型号导弹经过改装成为卫星发射不但可以节省卫星发射运载器的研制周期和经费，同时还可做到机动发射、应急组网。

目前，世界各国都对小卫星机动发射技术有所突破。例如，美国利用退役的“民兵-2”固体导弹一、二级和“飞马座-KL”火箭末修级改造成的“人牛怪”运载火箭[2]，能把340 kg的有效载荷送入740 km的太阳同步轨道，并可较其他火箭节省30%的发射费用；同时俄罗斯也将RS-18导弹和SS-25导弹改造成为呼啸号运载火箭[3]和起飞1号运载火箭[4]用于卫星发射。

本文研究的对象是弹载小卫星机动发射弹道设计与优化。以经典型号弹道导弹为例，通过改造导弹的末修舱，加装高集成紧耦合微卫星，在传统弹道导弹动力学模型的基础上，设计导弹飞行程序，最终实现卫星发射入轨。

1 基础力学模型

1.1 地球引力

地球引力场为有势力场[5]，地球外质点引力位函数为

(1)

式中:fM为引力常数地球;m和r分别为质量和质点到地心距离。

于是，引力加速度为

(2)

1.2 发动机推力

火箭发送机虽有液体固体之分，但其产生机理相同，所以其基本推力计算公式相同。在不考虑控制的情况下，弹体系Ozy1和Ozz1轴方向的推力可以直接去零，由于存在大气静压力，而发动机喷口上没有大气静压力，在燃气静压力和大气静压力的共同作用下，发动机推力[6]为

(3)

1.3 空气动力

对于高速飞行的导弹来说，其空气动力的产生机理与飞机机翼升力产生机理完全一样，与导弹的外部形状、姿态、速度、空气密度和飞行高度有关。只是作用在导弹的空气动力[7]是空间中的一个向量。其表达式为

R=CRqSm，

(4)

1.4 柯氏惯性力和牵连惯性力

柯氏惯性力[8]和牵连惯性力[9]是由于坐标系旋转产生，对导弹的作用力也很小。

柯氏惯性力在发射坐标系下的分量为

(5)

式中:Fcx，Fcy，Fcz为柯氏惯性力在发射系下分量；m为导弹实时质量；acx，acy，acz为柯氏惯性力产生的加速度。

(6)

(7)

牵连惯性力在发射坐标系下的分量为

(8)

式中：Fex，Fey，Fez为牵连惯性力在发射系下分量；aex，aey，aez为牵连惯性力产生的加速度。

(9)

(10)

2 弹载小卫星发射弹道优化模型

以经典型号弹道导弹为例，小卫星发射弹道包括一级飞行段、二级飞行段和自由段，达到目标轨道后，利用末修级发动机施加推力最终达到入轨条件，在飞行过程中，导弹按标准弹道飞行，其姿态角根据优化的飞行程序角变化。

2.1 导弹飞行程序设计

(1) 一级飞行程序

导弹一级飞行程序又可以分为垂直上升、程序转弯、跨声速飞行和一级分离4段[10]。由于导弹一级飞行处于稠密的大气层中，而且要经历跨音速等复杂情况。一般对一级飞行不做太大改动。一级飞行程序如下：

(11)

式中：

(12)

t1为导弹垂直上升段的时间；t2为程序转弯结束的时刻；t3为跨声速飞行段飞行结束的时刻；tk1为一级结束时刻；α为二级飞行攻角，其中α和a控制弹道的转弯速率；θ为弹道倾角。

(2) 二级飞行程序

本文中的二级飞行开始段已经飞至临近空间中上层，空气产生的阻力相对一级要小，控制也比一级容易，所以主要优化参数也都在二级段。将二级飞行分段线性化设计，具体如下：

(13)

(3) 自由段飞行程序

自由段飞行导弹已经飞出大气层，弹体处于无控制飞行状态，直至导弹达到目标轨道以及运动状态要求，末修发动机点火，最终完成小卫星入轨任务。在此过程中，飞行程序角保持不变。

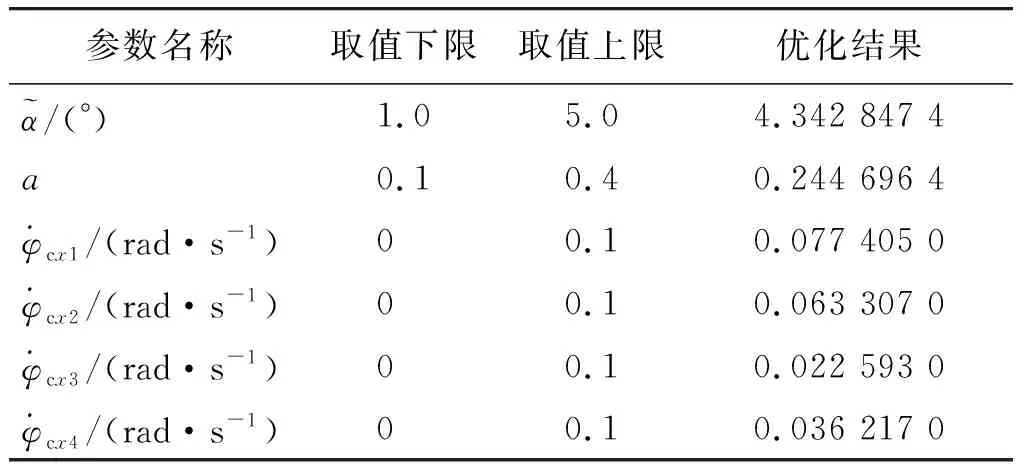
φcx(t)=φcx5，tk2

(14)

式中：φcx5为导弹二级飞行结束时的飞行程序角；tk3为自由段结束时刻即末修级点火时刻。

而后在末修级点火时刻tk3即弹道最高点，末修级点火实现微卫星增速入轨。

2.2 约束条件

卫星发射弹道优化的约束条件包含微分方程约束、路径约束和自由端结束状态约束等。

路径约束包括动压约束[11]和过载约束[12]等。具体表示如下：

(15)

式中：的q和ny分别为动压和过载；qmax和nymax分别为动压约束最大值和法向过载约束最大值。

自由段结束状态约束即末修级点火时刻约束，指的是末修级点火时卫星及末修级的位置与速度状态约束。形式如下：

(16)

式中：Θtk3为tk3时刻即末修级点火时刻导弹的当地弹道倾角；Θmax为当地弹道倾角的限定值；Htk3为tk3的轨道高度；Htar为目标轨道的轨道高度；Dev为轨道高度偏差限定值。

2.3 优化变量设计

本文研究的是利用经典型号的导弹改装后搭载发射小型卫星的弹道优化问题，整体设计弹道时需要优化的变量多，直接得到满足所有内点约束的全局最优解难度较大，因此合理的设计目标函数至关重要，本文对目标函数的设计主要包括以下几步：

由2.1节分析可得，卫星发射弹道优化的变量为

X= (x1,x2,x3,x4,x5,x6)T=

(17)

式中：x1，x2对应的是一级飞行程序转弯控制参数；x3，x4，x5，x6对应的是二级飞行转弯控制参数。

2.4 目标函数的设计

选择末修级发动机点火时刻的速度vf作为发射弹道优化的目标函数，即

F(X)=min{1/vf(X)}.

(18)

3 优化算法设计

遗传算法(genetic algorithms，GA)是一种基于基因遗传机制和自然选择的寻优算法[13]，其具体步骤包括：初代群体确立、求解适应度、依照适者生存原则和一定概率选择优良个体、在优良个体中随机交叉和变异后生成下一代群体，按照此法，群体逐代进化直至达到适应度要求或者满足进化代数要求便终止。

该算法的基本步骤如下：

(1) 种群初始化

(2) 适应度评价

运行弹道程序，计算各个种群的适应度值，使用轮盘赌法作为选择算子对这些个体进行排序筛选。

(3) 交叉

用A，B和A′，B′分别代表父代和子代的个体，运用下列方法进行交叉操作：

(19)

如果A′(B′)R，则A′(B′)=R。

(4) 变异过程

用C和C′分别表示父代和子代的个体，γ为(0,1)上均匀分布的随机数，k∈[0,1]为变异系数，U(0,1)为随机产生的整数0或1。

(5) 生成新一代种群

若满足迭代次数要求便输出最优解，否则继续上面的操作。

该算法的优化流程如图1所示。

4 仿真计算与结果分析

以经典型号导弹为例，利用遗传算法研究小卫星发射弹道优化设计问题。

(1) 参数设置

取发射点的大地经度Lf等于110.27°，取发射点的大地经度Bf等于33.04°，发射点高程为500 m；发射方位角10.425 8°。目标轨道定位450 km，当地弹道倾角限定值Θmax为1°。种群规模取40，进化代数取100，交叉概率取0.6，变异概率取0.01。

(2) 结果分析

给定后话变量的取值范围即满足其控制约束和过载约束，基于遗传算法进行弹道优化，最终得到优化变量的准最优结果，如表1所示。

表1 优化变量的结果

地心大地直角坐标系下卫星发射导弹弹道如图2所示。导弹飞行的高度随时间变化曲线如图3所示。导弹当地弹道倾角随时间变化曲线如图4所示。飞行程序角随时间变化曲线如图5所示。导弹速度随时间变化曲线如图6所示。仿真100代其适应度函数收敛曲线如图7所示。

由图1所示弹载卫星发射的轨道。由图7可见其适应度收敛曲线，遗传算法平均耗时2 782 s，搜索时间较快。

由图5所示弹载卫星发射的主动段的程序角。与传统的弹道导弹的主动段程序角[14]相比转弯速率更快，但并没有很大的差别而且满足其过载约束，进一步论证了将现有弹道导弹改装成为卫星发射运载器的可行性。

由图3,4,6可见，导弹的飞行的姿态和速度随时间变化而变化，主动段按照优化结果程序转弯，在主动段结束时达到速度最大值，而后进入自由段飞行，轨道高度不断增高，自由段开始当地弹道倾角随速度和位置变化而变化，本文优化目标为当地弹道倾角为零时的速度最大即当地弹道倾角为0时的速度最大。案例现实当地弹道倾角为0时速度达到6 000多m/s，处于临界入轨状态，而后末修发动机点火补充差速度，差速度计算方法由文献[15]提供，最终将小卫星推达入轨条件。

如图8所示，设定不同目标轨道高度下的末速度，随着目标轨道高度的不同能够达到的末速度也不同，在目标轨道高度设置为300～400 km时末速度为5 400 m/s左右；在目标轨道450 km左右达到末速度最大值6 100 m/s 左右，而后末速度随目标轨道的高度变高而变小。

5 结论

本文针对弹载入轨小卫星的弹道优化计问题，主要工作和研究结论如下：

(1) 本文建立了利用弹道导弹改装后发射小卫星的弹道优化模型。基于弹道优化模型，本文设计了卫星发射的弹道飞行程序。

(2) 在多约束、多阶段弹道飞行程序的基础上，以卫星能够精确入轨作为目标，利用遗传算法对模型进行求解，得出路径约束和末端约束下的优化变量最优解。

(3) 根据优化变量最优解，仿真得出卫星发射的发射轨道以及卫星入轨后的空间轨道。

(4) 本文论证了将末型号废旧导弹加装小卫星和末修级能够发射卫星的可行性，并提出弹载卫星发射的基础方案。

参考文献：

[1] 张凤立.我国应重视提高战争状态下卫星发射能力[J].航天工业管理,2000(1):46-47.

ZHANG Feng-li.China Should Atach Importance to Improving Satellite Launch Capability in the State of War[J].Aerospace Industry Managemengt,2000(1):46-47.

[2] 江山.“人牛怪”5发射月球探测器[J].太空探索,2013(11):36-38.

JIANG Shan.‘Minotaur5’Launch the Lunar Probe[J].Space Exploration,2013(11):36-38.

[3] 王乃洪,李华.俄罗斯的呼啸号运载火箭[J].中国航天,1997(6):17-18.

WANG Nai-hong,LI Hua.Russia′s Wuthering Rocket[J].Aerospace China,1997(6):17-18.

[4] 周威.前苏联运载火箭简介(六)[J].中国航天,2005(3):28-30.

ZHOU Wei.The Former Soviet Union Rocket Introduction[J].Aerospace China,2005(3):28-30.

[5] 孟嘉春,刘尚余.卫星重力梯度测量与地球引力场的精度研究[J].地球物理学报,1993(6):725-739.

MENG Jia-chun,LIU Shang-yu.Research on Accuracies for Satellite Gravity Gradiometry and Earth's Gravitational Field[J].ACTA Geophysica Sinica,1993(6):725-739.

[6] 周建军.导弹发动机推力曲线上浮现象分析与验证[J].弹箭与制导学报,2010,30(2):163-166.

ZHOU Jian-jun.Analysis & Verification of Thrust-Time Curve Rising of SRM[J].Missiles and Guidance,2010,30(2):163-166.

[7] 徐海江.导弹空气动力学[J].飞航导弹,1990(9):14-19.

XU Hai-jiang.Missile Aerodynamics[J].Aerodynamic Missle Journal,1990(9):14-19.

[8] 侯如松.惯性力是保守力吗?[J].大学物理,1989(11):47-27.

HOU Ru-song.Is Inertia a Conservative Force?[J].College Physics,1989(11):47-27.

[9] 孙智,冯有良.关于惯性力的讨论[J].集宁师专学报,2002(4):49-50.

SUN Zhi,FENG You-liang.Discussion on Inertial Force[J].Journal of Jining Teachers College,2002(4):49-50.

[10] 李振华,鲜勇,雷刚,等.基于种群熵粒子群优化算法的上升段交会弹道优化设计[J].导弹与航天运载技术,2015(6):96-99.

LI Zhen-hua,XIAN Yong,LEI Gang,et al.Launch Vehicle Ascent Rendezvous Trajectory Optimum Design Based on Population Entropy Based Particle Swarm Optimization[J].Missiles and Space Vehicles,2015(6):96-99.

[11] 国海峰,黄长强,丁达理,等.多约束条件下高超声速导弹再入轨迹优化[J].弹道学报,2013,25(1):10-15.

GUO Hai-feng,HUANG Chang-qiang,DING Da-li,et al.Re-Entry Trajectory Optimization for Supersonic Missile Considering Multiple Constraints[J].Journal of Ballistics,2013,25(1):10-15.

[12] 戴邵武,张亦农,曹凌.导弹过载控制设计方法研究[J].弹箭与制导学报,2004,19(S7):97-99.

DAI Shao-wu,ZHANG Yi-nong,CAO Ling.Study on Overload Control for Missile[J].Journal of Projectiles, Rockets, Missiles and Guidance,2004,19(S7):97-99.

[13] 金菊良,杨晓华,丁晶.标准遗传算法的改进方案——加速遗传算法[J].系统工程理论与实践,2001,21(4):8-13.

JIN Ju-liang,YANG Xiao-hua,DING Jing.An Improved Simple Genetic Algorithm-Accelerating Genetic Algorithm[J].Journal of Systems Science and Complexity,2001,21(4):8-13.

[14] 郝磊,李邦杰,王明海.速燃弹道导弹飞行程序角设计方法[J].弹箭与制导学报,2008(2):180-182.

HAO Lei,LI Bang-jie,WANG Ming-hai.Study on the Flight Program Angle Design of Ballistic Missile Based on Fast Burn Motor[J].Journal of Projectiles, Rockets, Missiles and Guidance,2008(2):180-182.

[15] 刁宁辉,刘建强,孙从容,等.基于SGP4模型的卫星轨道计算[J].遥感信息,2012,27(4):64-70.

DIAO Ning-hui,LIU Jian-qiang,SUN Cong-rong,et al.Satellite Orbit Calculation Based on SGP4 Model[J].Remote Sensing Information,2012,27(4):64-70.