Radon变换的雷达低慢小目标检测方法*

张宏伟，许道明，马俊涛，冉宏远

(陆军工程大学，河北 石家庄 050003)

0 引言

近年来，随着雷达隐身技术的持续发展以及低空突防战术的实战应用，低空微弱目标在军民领域带来的威胁与日俱增。尤其是随着军事需求的持续增长以及国民经济的快速发展，以无人机和轻型直升机等为代表的低空慢速小目标(以下简称“低慢小”目标)得到迅猛发展，由于此类目标具有飞行高度低、飞行速度慢以及自身散射截面积(radar cross section，RCS)较小等特点，其回波信号常常淹没于强地杂波中，且在多普勒域与慢速杂波信号混叠严重，致使防空预警雷达对其探测性能严重下降，给各国带来了重大安全威胁[1]。如何解决此类目标的有效探测已成为十分具有现实意义的研究课题。目前，国内外对“低慢小”目标的检测方法主要有以下几类：基于粒子滤波的TBD(track before detect)技术的检测方法[2-5]，基于微多普勒分析的检测方法[6]，基于多活性代理的系统检测方法[7]，以及基于杂波白化处理的检测方法[8]等。

在复杂的杂波环境通过有效的技术手段进行杂波抑制提高信杂/噪比(signal-to-clutter/noise ratio，CR/SNR)是“低慢小”目标检测必须面对的问题。由于Kalmus滤波器[9]能够在零频附近呈现较深止带凹口，并且随着频率增加呈快速上升，这一特性使其针对慢速目标检测时既可以有效的抑制强杂波又尽可能保留目标信息。而针对微弱目标检测，目前主要通过长时间观测，提高脉冲积累时间进而获得更好检测性能[10-12]。

本文在雷达长时间观测的基础上，首先对雷达回波数据进行Kalmus滤波预处理，继而通过Radon变换处理，在Radon参数空间完成目标检测。仿真数据结果表明，本文方法在很好地抑制了强地杂波的基础上，通过变换域处理的方法有效实现了“低慢小”目标的检测。

1 雷达“低慢小”目标回波信号模型

在不考虑干扰信号的情况下，一般认为雷达回波信号由目标回波信号、杂波信号、噪声信号3部分构成，则雷达回波信号可以理想的描述为

x(t)=s(t)+c(t)+n(t),

(1)

式中：s(t)为目标回波信号；c(t)为杂波信号；n(t)为噪声信号。

针对距离R处待测点目标反射回波进行模拟，其复信号可以表示为

Sr(t)=A0Gta(t-τ)exp[j2π(fc+fd)(t-τ)],

(2)

a(t)=rect(t/T)exp(jπμt2),

(3)

式中:rect(x)为矩形函数;μ=B/T为调频斜率;B为信号带宽;T为脉冲宽度。

基于上述模型进一步分析，由于此类目标飞行高度较低，雷达探测此类目标时需要考虑多路径干涉影响，图1为镜面反射影响的几何示意图。

图1中，ha,ht分别为雷达架高和目标高度;G1,G2分别为直射波和反射波对应的天线增益、直射波与反射波的波程差(km)。当综合多路径干扰和大气衰减影响时，防空雷达对于“低慢小”目标探测的回波功率为[13]

Ps=kσtFdF4(ε)/R4,

(4)

式中:k=PtG2γ2/((4π)3Ls)为雷达参数确定的常数，Pt为雷达发射功率，Ls系统传输损耗;F(ε)=2sin(πhaht/(γ/R))为传播因子;Fd=e-0.45δd为大气衰减因子。

已知目标回波信号的复信号为Sr(t)，其功率则可表示为

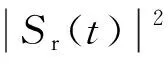
(5)

结合式(2)～(4)则目标回波信号可以进一步整理为

(6)

该目标模型综合考虑了多路径干涉、大气传输损耗以及系统损耗等因素，表征了目标飞行高度、飞行速度和RCS等特性对回波的影响。

2 Radon变换原理及特性

自1917年奥地利数学家J.Radon提出Radon变换以来,此变换已被广泛应用于物理、材料科学、天文等方面[14-16]。Radon变换是将图像变换为某一指定角度射线方向上投影的变换[17]，图2是以任一角度投影的示意图。在二维欧式空间中，一个连续二维函数的Radon变换定义如下[18]：

(7)

式中：D为积分图像平面；ρ为坐标原点到直线的距离；δ为dirac-delta函数;S(x,y)为点(x,y)的强度或亮度;(ρ,θ)为积分线的参数。

在图像中的每条线都在Radon参数域对应着一个比背景亮的峰，而暗线则对应着一个凹槽。正是基于Radon变换这样的性质，使“低慢小”目标检测问题从传统的时域或频域检测转化为对目标运动的时间-距离像进行Radon变换之后，在Radon参数域进行检测。

在长时间观测基础上，对雷达回波数据合并形成的二维函数S(t,r)直接进行Radon变换，则式(7)可以写成：

(8)

式中：S(t,r)为由雷达回波数据合并成的距离-慢时间像；t为慢时间域；r为距离域；D为距离-慢时间平面；ρ为原点到直线的垂直距离；θ是原点到直线的垂线与t轴的夹角[19]。

而目标的运动轨迹在Radon域与极角θ的对应关系为

(9)

式中:Δr为雷达距离分辨单元；vr为目标径向速度；PRF为雷达的脉冲重复频率(pulse repetition frequency，PRF)。

由于地杂波的运动速度与目标速度的差值在Radon参数域引起角度偏移量θ值的差异，因此在Radon参数域中将目标从杂波环境中检测出来。

3 基于Radon的雷达“低慢小”目标检测方法

传统方法通过对目标运动轨迹进行非相参积累提高SCR完成微弱目标检测，但是杂波与目标同时得到了积累，而且往往杂波能量强于目标，致使积累后检测依然存在很高的虚警率。所以对积累前的雷达回波数据进行Kalmus滤波抑制杂波以提高检测性能。

3.1 Kalmus滤波器设计

Kalmus滤波器可以通过离散傅里叶变换(DFT)等效的梳状滤波器来实现[20]，其响应函数为

(10)

式中：n=0,1,…,N-1，N为滤波器阶数，0≤k≤N-1为滤波器组的组号。

由DFT定义可以推导出其等效为一组滤波器组，Kalmus滤波器本质是将DFT滤波器组中的相邻两个滤波器相减获得深凹口，然后通过频域搬移使凹口落在零频。由此可得到Kalmus滤波器的幅频响应，如图3所示。

3.2 降维平滑处理

在雷达距离分辨率和雷达PRF都为确定参数情况下，从式(9)中可以看出，参数θ值随着目标运动速度的增加而增加，而由于“低慢小”目标本身速度值较小，其运动轨迹与杂波在Radon参数域对应的θ值区分度将很小，为了提高运动目标轨迹在Radon域的角度偏移量，对距离-慢时间像采取时域降维处理[21]。

已知距离-慢时间像为S(t,r)，对其沿慢时间维度进行补零处理，使处理后的时间维长度为N的整倍数，N的时域降维因子。处理后距离-慢时间像可以重新写为

(11)

对降维后的距离-慢时间像进行非相干叠加，以进一步平滑图像，即

(12)

对降维平滑后的距离-慢时间像进行Radon变换：

(13)

经过时域降维之后，低速目标在Radon域与极角的关系可以表示为

(14)

从式(14)中可以看出，由于“降维平滑”处理，目标运动轨迹在Radon参数域对应的偏移量θ值将明显增大，以更利于杂波中将目标检测出。

3.3 算法流程

基于以上理论基础，图4给出了基于Radon变换的雷达“低慢小”目标检测方法流程图，主要分为如下步骤:

步骤1：原始雷达回波数据处理。在雷达接收端，对接收到的雷达回波数据进行距离向解调和脉压处理，并将处理后数据进行存储。

步骤2：强杂波抑制处理。将经过预处理的单帧雷达回波数据通过Kalmus滤波器完成强杂波抑制处理。

步骤3：多帧联合数据降维平滑处理。

步骤4：距离-慢时间像进行Radon变换处理。

步骤5：门限检测。通过设置幅度和角度两级检测门限检测出目标。第1级设置幅度门限为T1，具体设置方法如下：

(15)

本文中值设为0.005。小于该门限值设置为0。第2级检测门限为角度检测门限θw，根据实际杂波速度设置，本次实验假设地杂波运动速度为5 m/s。

4 实验结果与分析

雷达系统与目标仿真参数设置如表1，2所示。

从图5中可以看出，经过Kalmus滤波器强杂波抑制处理后，多帧数据合成的雷达回波距离-慢时间像中，目标运动轨迹显现可见，说明杂波抑制处理有效。

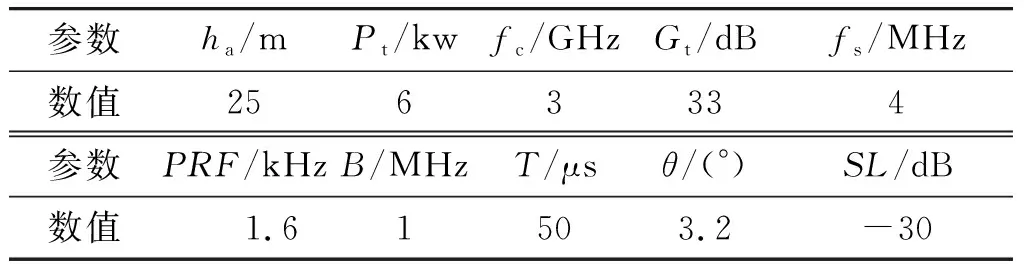
表1 雷达系统参数

表2 目标仿真参数

对为经过降维平滑处理的距离-慢时间距离像直接进行Radon变换，图6中看到在Radon参数域中，杂波与运动目标的角度偏移量区分不是特别明显，而图7所示，经过降维处理，降维因子为14，目标在Radon参数域与杂波区分明显。

由于地杂波运动速度非常低，降维平滑处理后其在Radon域的峰值点仍然在90°附近，通过在Radon参数域的设置的检测门限，检测结果如图8所示，可以很好地将“低慢小”目标与地杂波区分开，从而验证了本方法的有效性。

5 结束语

本文在Radon变换的基础上结合Kalmus滤波器提出一种针对“低慢小”目标的检测方法，首先通过对强地杂波进行抑制，有效提高了SCR/SNR的基础上，又通过Radon变换，在变换后的参数域中有效完成了目标检测，仿真结果验证了该方法的有效性。

参考文献：

[1] 李明明,卞伟伟,甄亚欣.国外“低慢小”航空器防控装备发展现状分析[J].飞航导弹,2017(1):62-70.

LI Ming-ming,BIAN Wei-wei,ZHEN Ya-xin.Analysis on the Development of Low-Altitude Slow Small Aircraft Control Equipment[J].Marling Missile,2017(1):62-70.

[2] LU J,SHUI P L,SU H T.Track-Before-Detect Method Based on Cost-Reference Particle Filter in Non-linear Dynamic Systems with Unknown Statistics[J].IET Signal Processing,2014,8(1):85-94.

[3] RUTTEN M G,GORDON N J,MASKELL S.Recursive Track-Before-Detect with Target Amp Latitude Fluctuations[J].IEE Proc.Radar,Sonar and Navigation,2005,152(5):345-52.

[4] HU Rui-qing,TIAN Jie-rong.Study on Tracking and Tracking Small and Slow Targets Using Particle Filter[J].Computer Knowledge and Technology,2014(19):184-186.

[5] DAVEY S J,RUTTEN M G,CHEUNG B.A Comparison of Detection Performance for Several Track-Before-Detect Algorithms[J].Journal on Advances in Signal Processing,2008(428036):1-10.

[6] 陆晨阳.雷达低速目标检测方法研究[D].西安：西安电子科技大学,2014.

LU Chen-yang.Research on Methods for Low Speed Target Detection of Radar[D].Xi′an ：Xidian University,2014.

[7] 张云佐.基于多活性代理的“低慢小”目标探测系统浅析[J].广西通信技术,2012(2):35-37.

ZHANG Yun-zuo.Analysis of Detection System for “Low，Slow and Small”Target Based on Multi Living-Agent[J].Journal of Guangxi Communication Technology,2012(2):35-37.

[8] 王党卫,秦江敏,马晓岩.基于杂波白化处理的海面低速弱目标检测[J].现代雷达,2003,25(6):15-18.

WANG Dang-wei,QIN Jiang-min,MA Xiao-yan.Clutter-Whitening-Based Low-Speed Weak Target Detection over the Sea[J].Modern Radar,2003,25(6):15-18.

[9] David K Barton,Sergey A.Leonov.Radar Technology Encyclopedia[M].Boston London:Artech House,1998.

[10] SKOLNIK M.Opportunities in Radar-2002[J].Electronics & Communication Engineering Journal,2002,14(6):263-272．

[11] 何嘉懿,廖桂生,杨志伟,等.一种参数化轨迹增强的TBD算法[J].西安电子科技大学学报,2015,42(6):17-22.

HE Jia-yi,LIAO Gui-sheng,YANG Zhi-wei,et al.Efficient Track-Before-Detect Algorithm Based on Parameterized Track Enhancement[J].Journal of Xidian University.2015,42(6):17-22.

[12] GROSSI E,LOPS M.A Novel Dynamic Programming Algorithm for Track-Before-Detect in Radar Systems[J].IEEE Transactions on Signal Processing,2013,61(10):2608-2619.

[13] 陈华伟,李侠,曹永辉,等.情报雷达低空小目标探测能力评估方法研究[J].空军雷达学院学报,2009,23(2):79-82.

CHEN Hua-wei,LI Xia,CAO Yong-hui,et al.Evaluation of Detection Capability of Low Altitude Small Target for Intelligence Radar[J].Journal of Air Force Radar Academy,2009.

[14] ZHOU Bin-zhong,STEWART A Greenhalgh.Linear and Parabolic Tau-p Transform Revisited[J].Geophysics,1994,59(7):1133-1137.

[15] NURUL KABIR M M,VERSCHUUR D J.Restoration of Missing Offsets by Parabolic Radon Transform[J].Geophysical Prospecting,1995,43:347-350.

[16] CARRETERO-MOYA J,GISMERO-MENOYO J．A Coherent Radon Transform for Small Target Detection[C]∥2009 IEEE Radar Conference,California，USA:IEEE Press，2009:1-4．

[17] REY M T,TUNALEY J K,FOLINSBEE J T.Application of Radon Transform Techniques to Wake Detection in Seasat-Asar Images[J].IEEE Trans.Geosci Remote Sens,1990,28(4):553-560.

[18] ANTHONY C Copeland,Gopalan Ravichandran,Mohan M.Localized Radon Transform-Based Detection of Ship Wakes in SAR Images[J].IEEE Transactions on Geoscience and Remote Sensing,1995,33(1):35-45.

[19] CARRETERO-MOYA J,GISMERO-MENOYO J,ASENSIO-LOPEZ A,et al.Application of the Radon Transform to Detect Small Targets in Sea Clutter[J].IET Radar,Sonar & Navigation,2009,3(2):155-166.

[20] 马晓岩.雷达信号处理[M].长沙:湖南科学技术出版社,1999:171-173.

MA Xiao-yan.Radar Signal Processing[M].Changsha:Hunan Science and Technology Press,1999:171-173.

[21] CHEN H,LI M,LU Y,et al.Novel Weak Target Detection Technique Based on Time-Dimension Reduced Multiple Frame Detection in the Radon Domain[J].Journal of Xidian University,2017,44(2):14-19.

[22] CARRETERO-MOYA J,GISMERO-MENOYO J,ASENSIO-LOPEZ A,et al.Application of the Radon Transform to Detect Small Targets in Sea Clutter[J].IET Radar,Sonar & Navigation,2009, 3(2):155-166.