改进加权SVC的雷达信号分选新方法*

袁泽恒，田润澜,张旭洲

(空军航空大学 航空作战勤务学院，吉林 长春 130022)

0 引言

雷达辐射源信号分选是将雷达侦察接收机截获的多部雷达信号，分成单部雷达信号的过程，是电子侦察系统和电子支援系统中的核心与关键[1]。传统的雷达辐射源信号分选主要基于脉冲重复间隔(PRI)以及其改进算法[2-3],当前也有利用脉冲到达时间差TDOA的分选方法[4]，随着雷达体制和电磁环境的日益复杂，基于PRI和TDOA的雷达信号分选正确率低。利用脉冲参数如载频(CF)、脉宽(PW)、脉幅(PA)、到达方向(DOA)[5-6],预先设定好一定的容差，经过多层次的相关处理，完成信号分选的结果可靠性差，而且产生增批的问题严重[7]。

为了克服上述方法的问题，基于多参数的雷达信号聚类分选得到广泛应用[8]，聚类是一种无监督的分类，不需要先验知识，有利于对未知雷达信号进行分选，弥补了现有雷达库数据不全的短板。常用的聚类方法有K-means方法[9]、模糊聚类方法[10]等，这些方法普遍存在复杂度高、类内耦合度和类间分离度低，导致分选结果准确率不高。

支持向量聚类(support vector clustering,SVC)是一种最为有效的无监督非参数型聚类方法[11-12]，但其算法的复杂度高，控制其聚类边界的参数惩罚因子C和高斯核宽度q的最优选取存在人为因素的影响。文献[11]采用支持向量聚类和分层互耦的算法，并结合熵的特征进行信号分选，但是熵的特征不是稳定的物理量，尤其是在识别聚类结果复杂度的时候，阈值的设置存在人为因素的影响。本文在文献[11]方法的基础上对数据样本和核函数内积进行加权，建立聚类结果有效评价模型，采用稳定的物理量作为聚类结果的度量值，提高分选的准确率。

1 支持向量聚类算法

支持向量聚类算法的基本原理是[13]：利用Gaussian核函数，将数据样本映射到一个高维特征空间中，并在这个高维特征空间中寻找一个能包围所有样本数据映射点的最优超球面，将这个超球面反映射回数据空间，最终得到包含所有数据点的等值线集。支持向量聚类(SVC)通过基于核函数的非线性映射，能够较好的分辨、提取并放大有用特征，融入松弛量后能有效排除孤立点和离群值，实现更为准确的聚类。

(1)

式(1)的Lagrangian函数为

(2)

式中:βj和μj均大于0，为Lagrangian乘子；常数C称为惩罚因子。

结合KKT条件，得出式(2)的Wolfe对偶形式：

(3)

引入Gaussian核函数：

(4)

式中：q为Gaussian核的宽度参数。

将核函数带入式(3)中得

(5)

对于每一个标准化的脉冲描述数据向量pdv″，其映射到特征空间中的像到球心的距离表示为

(6)

式中:当{pdv″|R(pdv″)=R}时，这时的标准化脉冲描述向量称为支持向量(SV)。由SV组成的等高面，能确定属于同一雷达辐射源参数的聚类边界。此后建立聚类标识关联矩阵，通过深度最优搜索(DFS)算法根据关联矩阵进行聚类分配。

在高脉冲密度的环境下，采用支持向量聚类进行分选，就会造成进行运算时关联矩阵规模庞大的问题，极大程度地降低其运算速度。文献[11]采用基于支持向量机的分层互耦聚类方法，对数据样本进行分层处理，很好地解决了上述问题。由于熵是不稳定的物理量，所以文献[11]采用类型熵调整聚类分选参数，会影响最优分选参数的选取，而且当雷达信号严重交叠时，采用文献[11]的方法进行分选的正确率显著下降。针对上述方法的不足，对其进行改进。

2 改进支持向量聚类

首先采用极值标准化对雷达信号数据进行预处理，将待聚参数标准化到同一维度上形成数据样本；然后利用变精度粗糙集计算数据样本的权重，对数据样本和支持向量机的核函数内积进行加权，稳定数据样本之间的平衡，从而避免聚类分选结果被参数的弱相关特征影响；最后对聚类结果进行分析，构建有效地评价模型，引入稳定的物理量来调整聚类分选参数，选取最优的聚类分选参数，提高分选的正确率。

2.1 参数标准化

DOA取值相对稳定，在分选时间内不会发生突变。因此通过已知雷达参数匹配后的数据进一步得到稀释。在脉冲描述字PDW中，CF和PW也相对稳定可以作为聚类参数。本文将雷达信号的到达角、载频和脉宽构成一个具有三维信息的雷达脉冲描述向量PDVi，i=1,2,…,n(n为总脉冲个数)。

原始的PDVi比较复杂，为排除原始PDVi中变量之间的量度不同对聚类效果的影响，需要对原始的PDVi进行标准化处理，使不同的参数分布在相同的区间[0,1]内，以相同的量级参与聚类。

对于n个脉冲信号，有m维特征参数，此时样本数据可以用如下表达式表示，脉冲描述向量PDVi=(pdvi1,pdvi2,…,pdvim)，这里m=3，PDVi=(DOAi,CFi,PWi)。先求出n个样本数据的第k维数据的均值和标准差为

(7)

(8)

其中，1≤k≤m，由此可得样本脉冲向量的标准化值

(9)

此时脉冲描述向量的标准化值不一定在区间[0,1]内，采用极值标准化公式：

(10)

2.2 加权处理支持向量聚类

针对不同类型的装备，测向精度和测频精度存在很大差异，不同类参数之间差异比较明显。同一类参数也存在类似问题，比如脉宽过窄，参数测量往往不准确，宽脉冲的区分度好，应当加大权重。对于上述问题，在SVC算法过程中为了降低弱相关对聚类结果准确性的影响，采用变精粗糙集对标准化后的样本数据进行处理，然后对核函数的内积进行加权[14]。

粗糙集理论中依赖度的定义：

(11)

式中：ci为属性参数；U为样本集序号;d为条件属性;β为误差参数。

将上述依赖度作为信号参数的重要度，即

(12)

该信号参数的权重为

(13)

在本文中只研究雷达信号辐射源的3个参数，即到达角、载频、脉宽。所以得到最优特征加权矩阵即

(14)

式中：aDOA，aCF，aPW分别为对应参数重要程度的加权系数。

SVC算法的加权计算公式如下：

(15)

考虑到雷达各辐射源属性，提高聚类结果的准确率，消除人为设置权重的影响，本文利用变精度粗糙集获取雷达辐射源各属性特征参数权重[15]，构成最优特征加权矩阵，该加权矩阵通过辐射源数据确定，完全利用了辐射源数据自身的特征，因此更加适用实际中雷达信号的聚类分选。

将式(14)中上述参量带入式(15)中可得

(16)

2.3 改进的支持向量聚类分选流程

在雷达辐射源信号分选中，所需处理的数据量很大，极大的影响其运算速度。文献[11]采用了支持向量机的分层互耦聚类方法，来解决此类问题。本文在文献[11]方法的基础上进行改进，具体步骤如图1所示。

从图1中可以看出，采用变精度粗糙集从已知雷达知识库中提取的样本信息进行分析，得到{DOA,CF,PW}各属性参数的最优特征加权矩阵，运用到支持向量机的核函数内积上，对其进行加权。此方法不会增加算法的时间复杂度，因为得到最优特征加权矩阵的步骤是事先完成的，所以不会延长聚类分选的时间。

2.4 聚类分选参数调节

本文将标准化处理的样本数据，脉冲描述向量pdv″作为研究对象，从类内耦合度和类间分离度出发，建立聚类结果有效评价模型，对聚类结果进行分析，从而确定最佳的聚类分选参数q和C。

类内耦合度通过聚类分选后样本的方差反映，方差越小，样本间波动就越小，即类内之间样本紧密程度就越高。

类内耦合度定义为

(17)

式中：ni为样本数，i为样本脉冲描述向量的维数。

对应的聚类分选后的样本中心为

(18)

分离度反映了不同类之间的差异性，定义为

(19)

(20)

分别将类内耦合度和类间分离度除以相应的权值，然后将两参数进行比较分析，建立对聚类分选结果的有效性评价模型：

(21)

式中：Cλ为对应阈值λ的类数。

G值越大，说明类与类之间的差异越大，聚类分选的结果也就越好。支持向量的聚类分选过程中，其聚类的边界受Gaussian核的宽度参数q和Lagrangian函数的惩罚因子C的控制。随着参数q的增加，聚类边界表现出更紧的特性。通过参数C的减少可以平滑聚类边界。采用文献[13]的分裂聚类方法，首先确定参数q的初始值为

(22)

在q的初始值下，会使Gaussian核函数的值偏大，导致聚类分选结果产生单一的聚类。在这种情况下取参数C=1，然后增大参数q的值，这样，单一的聚类开始分裂。随着q值增大到一定程度，聚类边界会变得粗糙，这时通过减少C值，用来平滑聚类边界。

文献[13]的方法面临的问题是如何确定最终的聚类分选结果，确定什么时候停止对聚类的分裂。文献[11]中利用类型熵随着信号复杂度的增加而增加的特点，进而对聚类结果分析，来确定最佳的聚类分选参数q和C的值，但是类型熵不是很稳定的物理量，所以采用类型熵调整聚类分选参数误差较大。为了解决上述问题，本文采用构建的有效性评价模型的参数G来保证门限确定的合理性，通过对多组聚类分选结果G值的计算，识别出较好的聚类分选结果，从而对其进行分析判断，来确定最佳的聚类分选参数q和C。

3 仿真实验结果及分析

为了验证本文方法的优势和有效性，对上述改进的多参数聚类分选系统进行了仿真实验。雷达参数的仿真数据如表1所示。

从表1中可以看出，4部雷达在不同属性的维度上均有重叠或部分重叠，而且雷达样本2和雷达样本3在到达角和脉宽参数上重叠比较严重，运用常规的分选方法，不仅不能使各雷达辐射源信号完全分开，还会产生信号大量增批和漏批的问题，从仿真数据中随机抽取400个样本，分别采用文献[11]的方法和本文上述方法进行聚类分选，实验仿真得出三维属性的雷达样本信号聚类结果分布图，如图2,3所示。

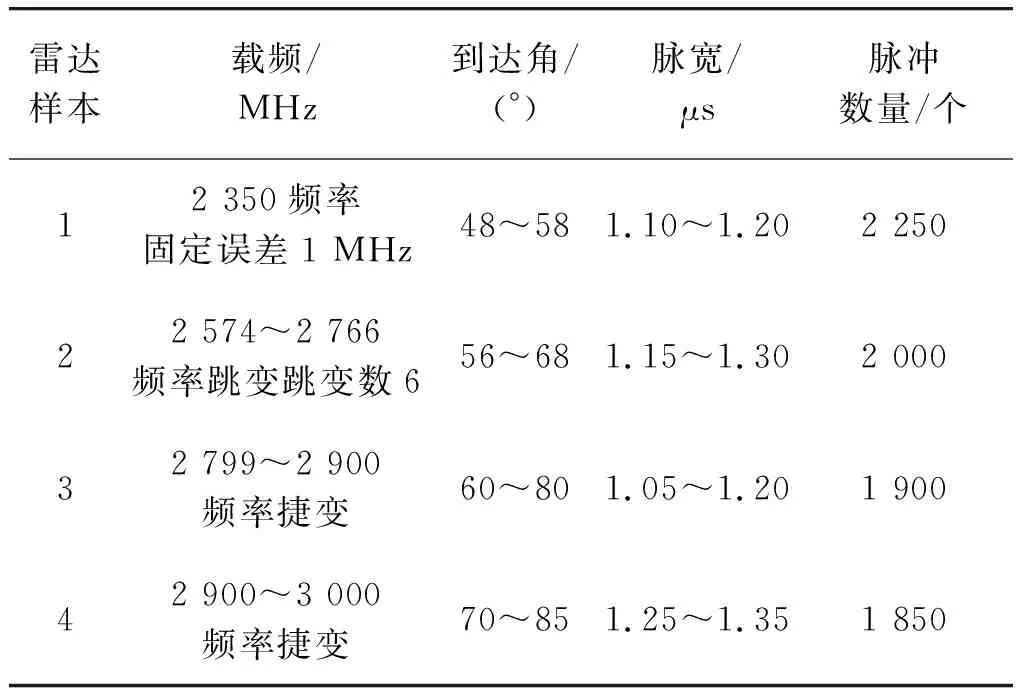
表1 雷达样本参数信息

可以从图2中直观地看出，在雷达样本2和雷达样本3的到达角和脉宽样本数据存在严重交叠的时，采用文献[11]的方法进行聚类分选的结果不够理想。

文献[11]是基于支持向量聚类和分层互耦的算法，并引入类型熵来调整聚类分选参数。从表2可以看出，这种方法对不交叠的或者部分交叠的信号，分选正确率高，当信号参数存在严重交叠的情况时，分选正确率会明显降低，而且引入的类型熵不是很稳定的物理量，用来调整分选参数存在一定的偏差。所以采用文献[11]的算法对仿真数据进行处理时，正确率只有96.8%。本文对上述方法进行了改进，首先对样本数据进行标准化，采用变精度粗糙集得出各属性参数的权值，对数据样本和支持向量的核函数内积进行加权，提高算法的鲁棒性，虽然这些都是预先完成的，不会增加算法的完成时间，但是增加了算法的计算量；然后建立对聚类结果的评价模型，引入稳定的参数G，调整最佳的聚类分选参数，提高分选的正确率，从表2中可以看出，本文方法对仿真数据进行处理时，正确率达到99.5%，可以验证改进算法的有效性。

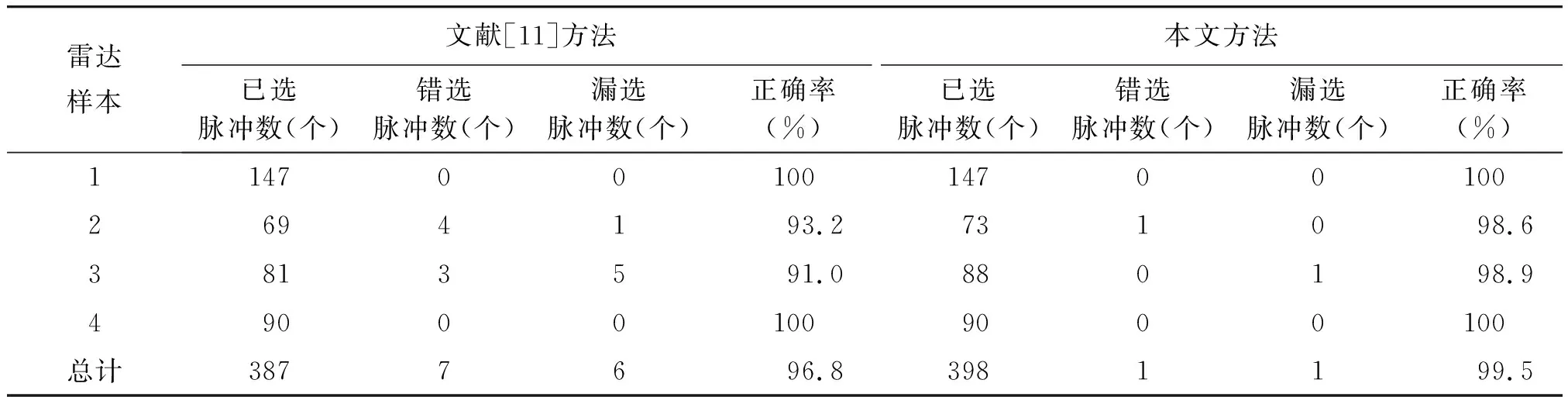
表2 2种方法的分选结果

4 结束语

本文通过采用变精度粗糙集，充分利用各属性参数自身的特点，获取各属性参数的权重，由其构成加权矩阵对雷达样本和SVC算法中的核函数内积进行加权，解决了数据之间存在不平衡和离群点的问题，从而避免被参数的弱相关特征影响其聚类分选结果。这个过程需要依赖数据库提前进行，虽然不增加算法的时间复杂度，但是算法的实时性不强。其次本文还通过构建有效评价模型，建立稳定的物理量调整聚类参数。仿真实验的结果验证了，当雷达信号严重交叠时，采用本文方法进行聚类分选时的正确率高，但是本文算法还存在很多不足，比如算法的复杂度高、时效性差、对数据库依赖性强等，下一步还需提高算法的时效性。

参考文献：

[1] 李合生,韩宇,蔡英武,等.雷达信号分选关键技术研究综述[J].系统工程与电子技术,2005,27(12):2036-2039.

LI He-sheng,HAN Yu,CAI Ying-wu,et al.Overview of the Crucial Technology Research for Radar Signal Sorting[J].Systems Engineering and Electronics,2005,27(12):2036-2039.

[2] NISHIGUCHI K ,KOBAYASHI M．Improved Algorithm for Estimating Pulse Repetition Intervals[J].IEEE Trans on AES,2000,36(2):407-421．

[3] 刘旭波,司锡才.雷达信号分选实现的新方法[J].系统工程与电子技术,2010，32(1):53-56.

LIU Xu-bo,SI Xi-cai.New Method for Sorting Radar Signals[J].Systems Engineering and Electronics,2010,32(1):53-56.

[4] 郑惠文,黄建冲.利用脉冲TDOA的雷达信号分选方法[J].现代防御技术,2017,45(2):217-222.

ZHENG Hui-wen,HUANG Jian-chong.Radar Signal Sorting Method Utilising Pulse TDOA[J].Modern Defence Technology,2017,45(2):217-222.

[5] 何明浩.雷达对抗信息处理[M].北京:清华大学出版社,2010.

HE Ming-hao.Radar Countermeasure Information Processing[M].Beijing:Tsinghua University Press,2010.

[6] 王宇.未知雷达信号PRI的快速分选识别算法研究[D].西安:西安电子科技大学,2010.

WANG Yu.Fast Sorting and Recognition Algorithm of Unknown Radar Signal PRI [D].Xi’an:Xidian University,2010.

[7] 赵葆昶,彭世蕤,郁春来,等.基于相参特性的雷达信号分选中“增批”问题研究[J].现代防御技术,2011,39(4):70-74.

ZHAO Bao-chang,PENG Shi-rui,YU Chun-lai,et al.Research on Increasing-Batch Problem in the Progress of Sorting of Signals Based on Coherency[J].Modern Defence Technology,2011,39(4):70-74.

[8] 郭杰,陈军文.一种处理未知雷达信号的聚类分选方法[J].系统工程与电子技术,2006,28(6):853-856.

GUO Jie,CHEN Jun-wen.Clustering Approach for Deinterleaving Unknown Radar Signals[J].Systems Engineering and Electronics,2006,28(6):853-856.

[9] 聂晓伟.基于K-Means算法的雷达信号预分选方法[J].电子科技,2013,26(11):55-58.

NIE Xiao-wei.Radar Signal Pre-Sorting Based on K-Means Algorithm[J].Electronic Science and Technology,2013,26(11):55-58.

[10] 尹亮,潘继飞,姜秋喜.基于模糊聚类的雷达信号分选[J].火力与指挥控制,2014,39(2):52-57.

YIN Liang,PAN Ji-fei,JIANG Qiu-xi.A Study on Sorting of Radar Signals Based on Fuzzy Clustering[J].Fire Control & Command Control,2014,39(2):52-57.

[11] 国强,王常虹,李峥.支持向量聚类联合类型熵识别的雷达信号分选方法[J].西安交通大学学报,2010,44(8):63-67.

GUO Qiang,WANG Chang-hong,LI Zheng.Support Vector Clustering and Type-Entropy Based Radar Signal Sorting Method[J].Journal of Xi′an Jiaotong University,2010,44(8):63-67.

[12] 王世强,张登福,毕笃彦,等.基于快速支持向量聚类和相似熵的多参数雷达信号分选方法[J].电子与信息学报,2011,33(11):2735-2741.

WANG Shi-qiang,ZHANG Deng-fu,BI Du-yan,et al.Multi-Parameter Radar Signal Sorting Method Based on Fast Support Vector Clustering and Similitude Entropy[J].Journal of Electronics and Information Technology,2011,33(11):2735-2741.

[13] BEN-HUR A,HORN D,SIEGELMANN H T,et al.Support Vector Clusteing[J].Journal of Machine Learning Research,2001,2(2):125-137.

[14] 吴连慧,秦长海,宋新超.基于加权SVC和K-Mediods联合聚类的雷达信号分选方法[J].舰船电子对抗,2017,40(1):13-17.

WU Lian-hui,QIN Chang-hai,SONG Xin-chao.Radar Signal Sorting Method Based on Weighting SVC and K-Mediods Combined Clustering[J].Shipboard Electronic Countermeasure,2017,40(1):13-17.

[15] 孙士保.变精度粗糙集模型及其应用研究[D].成都:西南交通大学,2005.

SUN Shi-bao.Study on Variable Precision Rough Set Model and Its Application[D].Chengdu:Southwest Jiaotong University,2005.