导弹武器系统精度类数据误差统计方法研究*

单时卓,张南，兰洪光，张艳

(1.中国人民解放军92941 部队，辽宁 葫芦岛 125000；2.北京电子工程总体研究所，北京 100854)

0 引言

防空导弹武器系统中末制导交班精度闭合是武器系统总体设计的关键环节之一，中末制导交班精度由多种误差合成，通常包括导弹初始姿态基准误差、捷联惯性测量装置误差、雷达测量误差、延时误差、导引头预定误差等[1-2]。上述误差中，雷达测量误差由于所占比重大，是最为重要的组成部分。因此，雷达测量误差分析是武器系统精度分析的重点[3]。

雷达测量误差包括距离误差、方位角误差、俯仰角误差、速度误差等，这些数据都具有很强的随机性，数据之间几乎没有相关性，属于导弹武器系统数据类型中的精度类数据。对该类数据分析，主要是分析误差特性，判断是否满足指标要求[4]。

在进行误差特性分析时，常用误差合成方法包括保守法、高斯法等。不同的误差合成方法可得出不同的误差统计结果。本文针对常用的误差合成方式，详细分析了每种误差合成方法得到的统计结果的范围，并利用某雷达实际检飞数据进行了验证。

1 测量误差及分类

在实际测量过程中，无论是直接测量的量还是间接测量的量，由于测量仪器、方法以及外界条件的影响等因素的限制，使得测量值与真值之间存在一个差值，该差值即为测量误差。测量误差按照不同的分类标准可以进行不同的分类，典型的分类标准包括按照误差产生的原因分类、按照误差性质分类等[5]。

1.1 按照误差产生原因分类

根据误差产生的原因，可将误差分为方法误差、环境误差、装置误差、处理误差。

(1) 方法误差。由于检测系统采用的测量原理与方法本身所产生的测量误差，是制约测量准确性的主要原因。

(2) 环境误差。由于环境因素对测量影响而产生的误差。例如环境温度、湿度、灰尘、电磁干扰、机械振动等存在于测量系统之外的干扰会引起被测样品的性能变化，使检测系统产生的误差。

(3) 装置误差。检测系统本身固有的各种因素影响而产生的误差。传感器、元器件与材料性能、制造与装配的技术水平等直接影响检测系统的准确性和稳定性产生的误差。

(4) 处理误差。检测系统对测量信号进行运算处理时产生的误差，包括数字化误差、计算误差等。

雷达测角方法、低空误差处理算法等会为雷达带来不同的方法误差。环境对雷达造成的误差主要有对流层折射、电离层折射和大气湍流等。与雷达设备有关的误差主要包括接收机噪声误差、电轴漂移、通道隔离度差、交叉极化耦合、饲服系统噪声等。处理误差主要有量化误差、滞后误差等[6]。

1.2 按照误差性质分类

根据误差性质，可将误差分为系统误差、随机误差、粗大误差。

(1) 系统误差。在重复条件下，对同一物理量无限多次测量结果的平均值减去该被测量的真值。系统误差大小、方向、恒定一致或按一定规律变化。

(2) 随机误差。测量值减去在重复条件下同一被测量无限多次测量的平均值。随机误差具有抵偿特性。产生原因主要是温度波动、振动、电磁场扰动等不可预料和控制的微小变量。

(3) 粗大误差。明显超过规定条件下预期的误差，它是统计异常值。应剔除含有粗大误差的测量值。产生原因主要是读数错误、仪器有缺陷或测量条件突变等[7]。

雷达测量误差的精确度是系统误差和随机误差的综合。考虑到防空导弹武器系统对雷达输出数据的不同需要，雷达测量的精确度又分为绝对精度和相对精度。

2 误差统计方法

误差统计是对不同性质的误差进行合成分析。在误差统计前，通常需要利用包括物理判别法、统计判别法等对粗大误差进行预先剔除处理，常用准则包括拉依达准则、格罗布斯准则等。因此，误差统计主要是按照不同的准则对系统误差和随机误差进行合成分析[8-9]。

假定系统误差和随机误差的标准差分别为Δ和σ，按标准差合成方法，测量误差可以表示为

(1)

式中：ρ为系统误差和随机误差间协方差；a1和a2为对应的误差传播系数。

根据系统误差和随机误差相关性的不同，误差统计方法又可以分为保守法和高斯法[10]。

2.1 保守法

若系统误差和随机误差完全相关，即ρ=1，则测量误差可以表示为

E=a1Δ+a2σ.

(2)

式(2)即为保守法。假定传播系数均为1，则上式可简化为

E=Δ+σ.

(3)

实际使用中，通常在随机误差中增加一个系数p，即

E=Δ+pσ.

(4)

保守法认为随机误差与系统误差是正相关的，即相关系数ρ=1，测量误差是系统误差与随机误差的迭加，因而是最安全的估计方法。保守法常常被选用，例如美国国家标准局就采用保守法进行误差综合，因为保守法是比较谨慎的。

2.2 高斯法

若系统误差和随机误差完全不相关，即ρ=0，则测量误差可以表示为

(5)

式(5)即为高斯法。假定传播系数均为1，则上式可简化为

(6)

实际使用中，通常在随机误差中增加一个系数p，即

(7)

高斯法认为随机误差与系统误差是完全不相关的，即相关系数ρ=0，测量误差中系统误差与随机误差可能有相互抵消的现象，是偏小的估计。由于是数学家高斯首先提出的，故又称高斯法。

2.3 误差分析方法小结

对于以上2种误差合成方法，在实际使用时，系数p的典型值取为1～3。不失一般性，本文主要分析p=1和p=3时的统计结果。不同合成方法具体含义如表1所示。

表1 P为不同取值时的误差合成方法及其含义

3 误差分析方法的统计结果分析

为分析方便，不妨假设在测量误差中，系统误差和随机误差的比例如下[11]：

Δ=kσ，

(8)

式中：k为系统误差和随机误差的比例系数，该比例系数可能随测量的不同而改变。

3.1 合成方法1

合成方法一得到的统计结果为[12-13]

P=Φ(|k|-k+1)-Φ(-|k|-k-1)，

(9)

式中：Φ(x)为标准正态分布函数。

图1给出了概率与k的关系示意图。

当k≥0时，

P=Φ(1)-Φ(-2k-1)，

(10)

当k<0时，

P=Φ(-2k+1)-Φ(-1).

(11)

可以得出，当k=±∞时，Pmax=0.841 3，当k=0时，Pmin=0.682 7。

在合成方法1进行误差分析时，不难看出，在总误差一定的情况下，概率结果随系统误差和随机误差间比例系数的不同而发生变化。当k=±∞时，即总误差仅由系统误差组成时，概率最大为0.841 3；当k=0时，即总误差仅由随机误差组成时，概率最小为0.682 7。特别的，当k=±1时，即系统误差和随机误差比例系数为1时，概率为0.840 0。

3.2 合成方法2

合成方法2得到的统计结果为

P=Φ(|k|-k+3)-Φ(-|k|-k-3).

(12)

图2给出了概率与k的关系示意图。

当k≥0时，

P=Φ(3)-Φ(-2k-3).

(13)

当k<0时，

P=Φ(-2k+3)-Φ(-3).

(14)

可以得出，当k=±∞时，Pmax=0.998 7 当k=0时，Pmin=0.997 3。

在合成方法2进行误差分析时，不难看出，在总误差一定的情况下，概率结果随系统误差和随机误差间比例系数的不同而发生变化。当k=±∞时，即总误差仅由系统误差组成时，概率最大为0.998 7；当k=0时，即总误差仅由随机误差组成时，概率最小为0.997 3。特别的，当k=±1时，即系统误差和随机误差比例系数为1时，概率为0.998 6。

3.3 合成方法3

合成方法3得到的统计结果为

(15)

图3给出了概率与k的关系示意图。

图3得出，当k=0时，可得Pmax=0.682 7，当k=±∞时，可得Pmin=0.5。

在合成方法3进行误差分析时，不难看出，在总误差一定的情况下，概率结果随系统误差和随机误差间比例系数的不同而发生变化。当k=±∞时，即总误差仅由系统误差组成时，概率最小为0.5；当k=0时，即总误差仅由随机误差组成时，概率最大为0.682 7。特别的，当k=±1时，即系统误差和随机误差比例系数为1时，概率为0.652 8。

3.4 合成方法4

合成方法4得到的统计结果为

(16)

图4给出了概率与k的关系示意图。

由图4可以看出，当k=0时，Pmax=Φ(3)-Φ(-3)=0.997 3；当k=±∞时，可得Pmin=0.5。

在合成方法4进行误差分析时，不难看出，在总误差一定的情况下，概率结果随系统误差和随机误差间比例系数的不同而发生变化。当k=±∞时，即总误差仅由系统误差组成时，概率最小为0.5；当k=0时，即总误差仅由随机误差组成是，概率最大为0.997 3。特别的，当k=±1时，即系统误差和随机误差比例系数为1时，概率为0.984 7。

3.5 小结

表2给出了不同合成方法所得统计结果的范围[14]。

表2 不同合成方法得到的统计结果的范围Table 2 Scope of the statistical results by different synthetic methods

表3给出了不同合成方法得到的统计结果的范围的典型值。

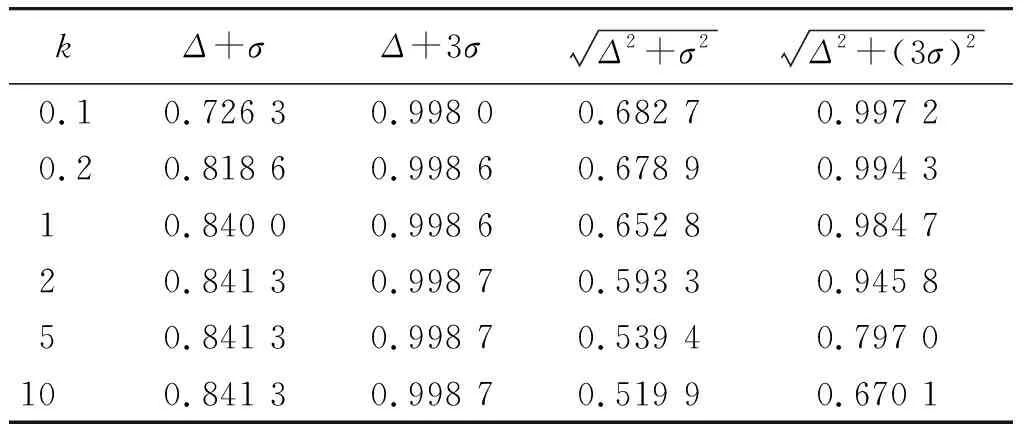
表3 不同合成方法得到的统计结果的典型值Table 3 Typical values of the statistical results by different synthetic methods

可以看出，合成方法1的取值在0.682 7～0.841 3之间，合成方法2的取值在0.997 3～0.998 7之间，合成方法3的取值在0.500 0～0.682 7之间，合成方法4的取值在0.500 0～0.997 3之间。上述4种合成方法中，合成方法2得到的统计结果其变化范围最小，而合成方法4得到的统计结果其变化范围最大。

4 实际检飞数据分析

由于雷达检飞数据通常认为近似服从高斯分布，不失一般性，利用某雷达检飞实测数据，统计系统误差和随机误差的比例系数，得到不同合成方法的理论统计结果，并与实际统计结果进行对比。表4给出了采用不同的合成方法时，雷达测量误差所得结果的概率的理论值与实际测量值的对比。测量误差包括：斜距、方位、俯仰、速度。

由表4可以看出，实测数据统计结果与理论值比较吻合，由于理论值是在误差服从高斯分布的前提下得到的，实测数据通常认为是近似服从高斯分布，因此不同合成方法的概率的理论值和实测值并非完全相等[15]。

Δ+3σ误差合成方法的概率变化范围最小，可以在不确定系统误差和随机误差相互关系的前提下，给出较为准确的概率结果，因此也建议优先选用该方法进行误差统计分析。

表4 不同合成方法理论与实测数据对比

5 结束语

本文分析了武器系统精度类数据的误差合成方法，得到了不同合成方法所对应的统计结果及其变化范围，并利用某雷达检飞数据进行了验证，理论结果与实测结果吻合较好。

若在预先不能确定系统误差和随机误差比例系数时分析武器系统精度链，由于合成方法2得到的统计结果的变换范围最小，因此建议优先选用该方法；由于合成方法4得到的统计结果的变换范围最大，应避免选用该方法。

参考文献：

[1] 陈怀瑾,吴北生,梁晋才,等.防空导弹武器系统总体设计和试验[M].北京:中国宇航出版社,1995.

CHEN Huai-jin,WU Bei-sheng,LIANG Jin-cai,et al.Overall Design and Test of Air Defense Missile Weapon System[M].Beijing:China Astronautics Press,1995.

[2] 刘海军,王丽娜.复合制导防空导弹中末制导交班问题研究[J].现代防御技术,2006,34(2):29-33.

LIU Hai-jun,WANG Li-na.Study on Handover Problem of Compound Guidancem Iissile Weapon[J].Modern Defence Technology,2006,34(2):29-33.

[3] 钱波,韩林频,齐润东.低空情况下中末制导交班问题解决方案探讨[J].现代防御技术,2010,38(4):31-34.

QIAN Bo,HAN Lin-pin,QI Run-dong.Analysis of Scheme to Solve Handover Problem in Low Altitude Situation[J].Modern Defence Technology,2010,38(4):31-34.

[4] 朱莉,张国权,高向军.导引头交班精度的雷达误差分析[J].火控雷达技术,2008,37(2):14-17.

ZHU Li,ZHANG Guo-quan,GAO Xiang-jun.Radar Error Analysis of Seeker′s Handover Accuracy:[J].Fire Control Radar Technology,2008,37(2):14-17.

[5] 丁鹭飞.雷达原理[M].西安:西安电子科技大学出版社,2002.

DING Lu-fei.Radar Principle[M].Xi′an:Xidian University Press,2002.

[5] 黄槐,齐润东,文树梁.制导雷达技术[M].北京:电子工业出版社,2008.

HUANG Huai,QI Run-dong,WEN Shu-liang.Guidance Radar Technology[M].Beijing:Publishing House of Electronics Industry,2008.

[7] 刘志平.检测仪表中粗大误差的剔除分析[J].电子测量技术,2009(11):55-57.

LIU Zhi-ping.Treatment Analysis of Rough Error About Measurement Instrument[J].Electronic Measurement Technology,2009(11):55-57.

[8] 盛骤,谢式千,潘承毅,等.概率论与数理统计[M].4版.北京:高等教育出版社，2008.

SHENG Zhou,XIE Shi-qian,PAN Cheng-yi,et al.Probability Theory and Mathematical Statistics[M].4th ed.Beijing:Higher Education Press,2008.

[9] 邓健,漆光平,刘鹏,等.武器试验数据处理及管理系统的研究[J].导弹与航天运载技术,2014(4):46-49.

DENG Jian,QI Guang-ping,LIU Peng,et al.Research of Data Processing and Management System for the Weapon Test[J].Missiles and Space Vehicles,2014(4):46-49.

[10] 武红霞.雷达动态性能检验和精度鉴定方法[D].南京:南京理工大学,2008.

WU Hong-xia.Method of Radar′s Proof-Test of Dynamic Quality and Appraisal of Precision[D].Nanjing:Nanjing University of Science and Technology,2008.

[11] 张淑丽，叶满昌.导弹武器系统仿真可信度评估方法研究[J].计算机仿真,2006,23(5):48-52.

ZHANG Shu-li,YE Man-chang.Simulation Credibility Evaluation Method for Missile Weapon System[J].Computer Simulation,2006,23(5):48-52.

[12] 陈岳隆,刘连忠.误差分析在数传指挥引导系统中的应用研究[J].计算机技术与发展,2006,16(7):180-182.

CHEN Yue-long,LIU Lian-zhong.Application Research of Error Analysis in Interception Guidance Automatic System Based on Data-Link[J].Computer Technology and Development,2006,16(7):180-182.

[13] 姚熊亮,陈海龙,赵新,等.基于拉依达准则的舰载设备抗冲击薄弱环节判定[J].中国舰船研究，2007,2(5):10-14.

YAO Xiong-liang,CHEN Hai-long,ZHAO Xin,et al.Weak Link Determination of Anti-Shock Performance of Shipboard Equipments Based on Pauta Criterion[J].Chinese Journal of Ship Research,2007,2(5):10-14.

[14] 林洪桦.测量误差与不确定度评估[M].北京:机械工业出版社,2009.

LIN Hong-hua.Measurement Error and Uncertainty Evaluation[M].Beijing:Machinery Industry Press,2009.

[15] 程健庆.仿真建模技术在新型舰炮武器系统试验中的应用[J].计算机仿真,2002,19(1):54-58.

CHENG Jian-qing.Application of Simulation and Modeling Technology in New Type Naval Gun Weapon System Test[J].Computer Simulation,2002,19(1):54-58.