滑枕热伸长补偿的建模及编程

■ 齐齐哈尔二机床（集团）有限责任公司设计院 （黑龙江 161005） 陈雪芳 崔凤有

1. 补偿基本原理介绍

该机床采用滑枕移动式结构，即主传动系统安装在主轴箱箱体内，主轴箱采用整体式包容结构，将滑枕包容在箱体内。铣轴装在方滑枕内带动镗轴旋转，镗轴可在铣轴内水平自由移动。滑座与床身的导轨、立柱与主轴箱导轨以及滑枕与主轴箱的导轨之间采用恒压闭式静压导轨。温度传感器布置点最终确定在主轴前后轴承及滑枕与主轴箱导轨立面与水平面的静压油膜处，主轴轴承布置三个温度传感器，分别测量三个主轴轴承的温度；滑枕与主轴箱导轨副立面及水平面各布置一个温度传感器，用来测量液压油膜的温度，一共采集5处温度值。在主轴转速250r/min及450r/min两种最常使用的转速下进行温度采集以及滑枕镗轴的Y向、Z向热伸长量的变化值。

从主轴转速250r/min及450 r/min两种常用工况下进行的试验可以看出（见图1、图3），在机床工作达到稳定状态期间，机床5点测量温度基本都是呈线性曲线上升的，在工作2.5～3h以后，机床温度趋于稳定；主轴转速在450r/min时温升要比250r/min时要大，同时用于产生的热量也比较大；前轴承与后轴承测量点温度曲线起点相同，近似线性曲线上升，二者温度曲线分别用参数T1、T2表示，中轴承与水平导轨面油膜温度变化曲线重合，同时垂直导轨油膜温度变化曲线与二者平行，并且三者温度变化基本为线性上升，由于建立数学模型变量为温度差值，因此三者采用用同一参数T3表示。

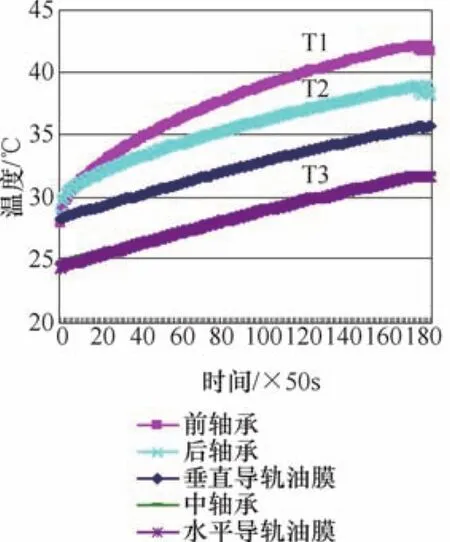
图1 主轴转速250r/min测量点温度曲线

从图2、图4所示可以看出Z向热误差基本呈线性上升，Y向热误差基本呈线性下降，上升或下降表示偏移的方向；从图2及附表中可以看出在试验时间180min内，镗轴Z向偏差为0.13mm，Y向偏差为0.069mm；从图4及附表中可以看出相同情况下，镗轴Z向偏差为0.2mm，Y向偏差为0.05mm，镗轴Z向热误差变化幅度较大，镗轴Y向热误差变化幅度较小。主轴转速250r/min及450r/min各点温度变化范围及镗轴热误差见附表。

2. 数学模型建立

图2 主轴转速250r/min热误差曲线

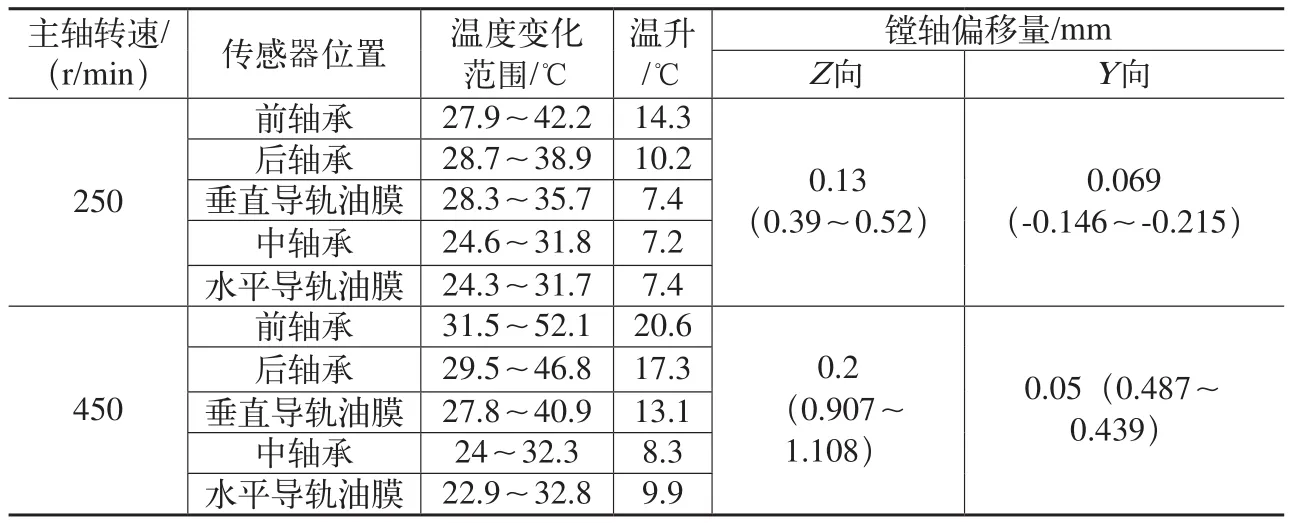
主轴转速250r/min及450r/min各点温度变化范围及镗轴Z、Y向热误差表

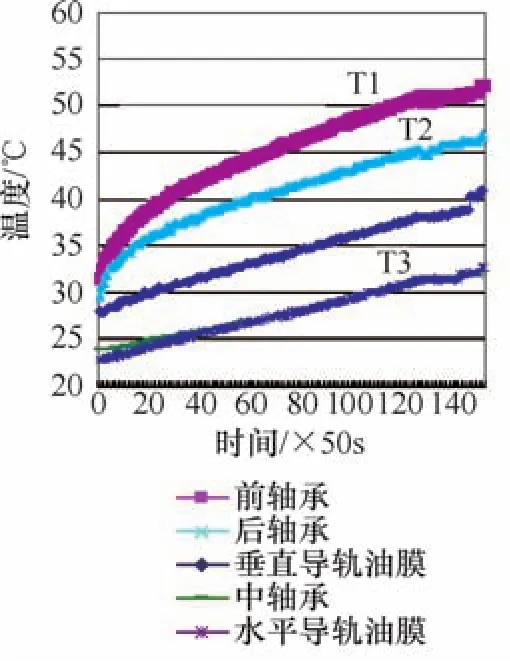
图3 主轴转速450r/min测量点温度曲线

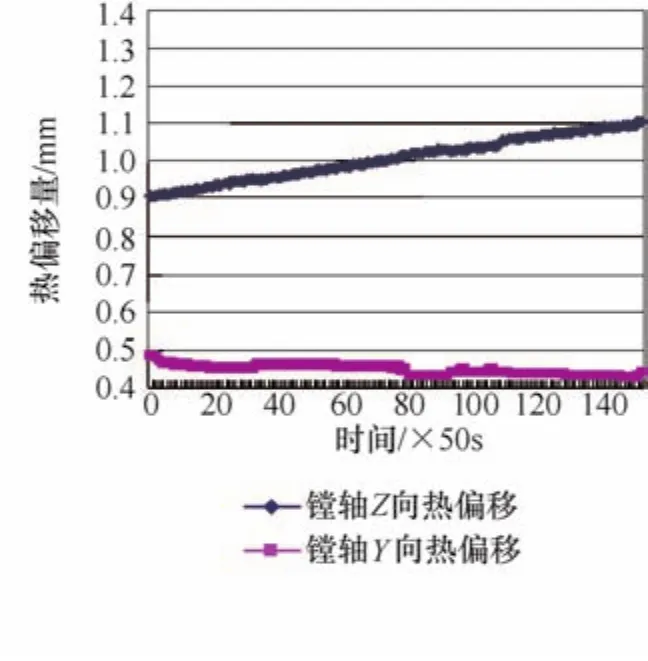
图4 主轴转速450r/min热误差曲线

根据主轴转速250r/min、450r/min测量点温度曲线图，如图1、图3可知，前轴承与后轴承测量点温度曲线起点相同，呈抛物线形状，二者温度变量分别采用ΔT1、ΔT2表示；中轴承和水平导轨面油膜温度变化曲线重合，同时垂直导轨油膜温度变化曲线与二者平行，并且三者温度变化成线性，由于建立的数学模型采用温度差值变量的形式，因此三者采用同一变量值ΔT3可满足建模要求。

数学模型采用共线性数学公式和权重数学公式分别进行建立。第一种共线性数学公式如下：

式中，E为热误差（mm）；ΔT1为前轴承测量点温度（℃）；ΔT2为后轴承测量点温度（℃）；Δ T3为中轴承、水平导轨面油膜和垂直导轨油膜测量点温度（℃）；a1、a2、a3为常数。

主轴转速250r/min的轴向误差Ezs、Y向误差Ey分别与温度变量拟合公式如下，其中公式中常数根据附表中主轴转速250r/min，各测量点热误差与温度采集表中数据求得：

式中，为主轴转速250r/min的轴向误差（m m）；为主轴转速250r/min的垂向误差（mm）。

主轴转速450r/min的拟合公式如下，其中公式中常数根据附表2 主轴转速450r/min各测量点热误差与温度采集表中数据求得：

从以上建立的数学模型可以看出，得到四组常数不同的热误差与温度变化的函数关系式，如果用这四组函数关系式编写程序比较繁琐，实际机床精度补偿调试过程也会很困难，因此采用第二种权重方法进行数学建模，其数学公式如下：

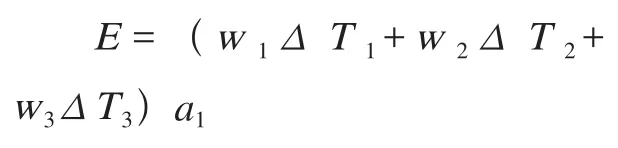
式中，w1、w2、w3为常数。

权重函数关系式包含了250r/min和450r/min两种主轴转速下热误差与温度变量函数关系，通过代入实际的温度变量数值，并且进行权衡得到w1、w2、w3及a1的数值，最后所建立的数学模型如下：

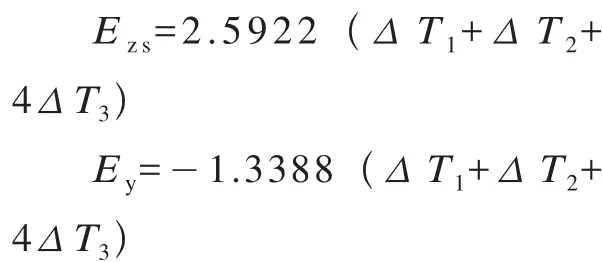
式中，Ezs为主轴转速4 5 0 r/min的轴向误差（mm）；Ey为主轴转速450r/min的垂向误差（mm）。

3. 补偿程序编写

该机床采用西班牙FAGOR公司8055M型数控系统，基于8055M PLC语言的补偿程序设计如下：

4. 结论

经过补偿后的测试结果看，主轴转速250r/min，镗轴Z向偏差为从0.13mm减小到0.051mm，Y向偏差从0.0 6 9 m m减小为0.026mm；主轴转速450r/min，镗轴Z向偏差从0.2m m减小到0.052mm，Y向偏差从0.053mm减小到0.027mm，镗轴Z向和Y向热伸长变化幅度很小，补偿效果比较好。

：

[1] 崔凤有，陈雪芳，李德刚. 一种滑枕热伸长补偿方法在数控落地铣镗床中的试验分析 [J]. 制造技术与机床，2013（10）：65-67.

[2] 王建平. 组合预测权重计算公式的探讨 [J]. 预测，1993（4）：54-55.

[3] 林海波. PLC编程技术探讨 [J].长春工程学院学报（自然科学版），2001，2（3）：70-72.