压气机特性曲线多项式回归拟合方法

代 星，赵元松，岳永威，吴 垚

（1. 91054部队，上海 200235；2. 中国航空综合技术研究所，北京 100028；3. 92602部队，上海 201900）

0 引言

舰用燃气轮机作为舰船动力系统的核心装置，其起动、调节、变速的特性在很大程度上影响着舰船的运行。压气机是燃气轮机的主要部件，其特性对于仿真结果有显著影响。在实际使用过程中，压气机不可能固定在额定工况下工作，舰船运行时复杂的变化（如负荷降低、温度或压力变化、叶片结垢或磨损导致的零部件性能变化等）都会造成压气机偏离原稳定工况，因此了解压气机关键参数的变化规律对于把握压气机的性能十分重要。但是，通过试验获取压气机特性的方法不仅费用较高，而且难以全面反映所有转速特性；实际中仅能够获得部分工况的数据，且这些数据多以离散点或者曲线图的形式存在。如何由有限的数据和图表模拟及预测压气机未知运行状态成为了一个难点。

由于压气机特性表现出较强的非线性，采用常规的线性插值方法模拟往往导致模拟结果精度较差，因此，国内外学者提出了一些模拟压气机特性的方法，如神经网络算法[1-3]、模糊辨识法[4]、滑动最小二乘法[5]和偏最小二乘法[6]等。这些算法能够较好地逼近压气机特性曲线，但仍存在一些不足。神经网络法能够在理论上与实测值高效逼近，但在插值效果上始终存在问题；模糊辨识法相较神经网格法拟合精度较差，对于未知数据的插值能力仍需进一步研究验证；滑动最小二乘法和偏最小二乘法能够控制压气机特性曲线的精度，但计算量较大、算法复杂度高。

本文首先对压气机特性进行理论分析，对同一转速下的试验数据分别进行线性插值拟合，通过分析拟合效果，再对不同转速下的拟合系数进行线性插值拟合，结合两部分拟合函数，最终获得压气机特性曲线函数。

1 压气机的插值计算

压气机特性曲线包括转速（n）、效率（η）、流量（G）和压比（π）四个参数量。压比和效率用流量和转速可以表示为

压气机出厂前通常会对其进行测试，记录某些转速下的压比、流量和效率的数据点，如图1所示。若仅有压气机曲线图，则需要作辅助线来获取数据，如图2所示。记录压气机的各转速曲线（如图2中的n1～n4），做若干条辅助线（如图2中L1～L4）与转速曲线相交，记录各辅助线与转速曲线相交点的增压比、流量和效率。

图1 压气机特性曲线离散数据点

图2 通过辅助线获取特征数据

由于这些数据不可能涉及所有运行中的转速，因此需要在工作中根据已有数据推算其他未知转速下的压气机特性。基于已有试验数据进行压气机特性曲线拟合就是结合已有的数据条件推测未知的数据条件，而目标转速值在已知数据的转速范围内。由公式（1）和公式（2）可知：压气机的压比和效率都需要双变量参数表达，因此需要通过进行两次插值计算才能确定，本文选用π/η-G，G-n的插值方式。

2 压气机特性曲线逼近方式

对于相同转速的曲线点，可以直接用高次幂的多项式进行拟合。由于不同转速曲线形状相似，且各个曲线随转速渐进变化的规律也是近似的，所以可以用同一多项式逼近。以压比作为因变量，转速和流量作为自变量，先做某一转速下关于流量的多项式曲线拟合，用最小二乘法进行精度逼近[7]，拟合多项式为

式中：iπ为转速ni(i=1,2,3,…,p)下的压比因变量；aji(j=0,1,2,3,…,q)为转速ni下的多项式系数。通过比较不同多项式的拟合残差获得最佳的多项式，从而固定q值。之后做多项式系数aji(j=1,2,3,…,q)关于转速ni(i=1,2,3, …,p)的多项式拟合，拟合代数多项式为

式中：bji(j=1,2,3,…,k)为多项式系数。结合公式（3）和公式（4），即可得到压比关于转速和流量的表达式。

3 压气机特性曲线拟合过程分析

本文选取文献[8]附录中压气特性数据做压气机曲线拟合，其中转速、增压比、流量均为相对转换值（为保证相同转速下压比、效率取值的唯一性，删除表格中部分同转速下不同流量值对应的数值相同的压比、效率列，以保证合理性），具体数据如表1所示。

表1 压气机相对速度、相对压比、相对流量和效率数据值表

首先应用R函数工具箱和公式（1）对固定转速下的压比和流量进行第一步曲线拟合，通过重复对比不同次数下的多项式拟合精度，发现q=3时，拟合精度足够，拟合误差小，得到的结果与原数据最接近、残差最小，因此根据公式（3）固定第一步压比-流量多项式的次数为3。然后将第一步拟合的多项式不同转速下的系数取出，以转速ni(i=1,2,3,…,p)为自变量参照公式（4）进行第二步拟合，在拟合的过程中，通过R函数工具箱对系数的拟合残差进行检验，与第一步拟合需要固定多项式次数不同，第二步拟合各系数的多项式次数可以不同，以拟合的精度最低为标准进行选取。参照公式（4），系数与转速的多项式形式与精度的检验结果如表2所示。

表2 系数多项式拟合评估表

由表 2可以看出：系数多项式拟合的残差绝对值基本都在0.1以内，说明系数多项式拟合效果较好。参照表2，通过两步多项式拟合，压比与流量、转速的多项式拟合的最终结果为

在表1中同转速列上取三个点，经拟合公式（5）计算得到压比，与表 1中同转速下相同流量对应的压比进行比较，结果如表3所示。

表3 压比拟合对照表

由表 3可以看出：压比拟合相对误差最多不超过3%。图3为压比拟合对照图，原压比-流量曲线与拟合出的压比-流量曲线基本贴合，曲率误差较小、精度较高。同理，效率与流量、转速的多项式拟合的最终结果为

在表1等转速列上取三个点，经拟合公式（6）拟合得到效率，与原表1在相同流量下对应效率进行比较，结果如表4所示。由表4可以看出：效率拟合误差最多不超过5%。图4为效率拟合对照图，原流量-效率曲线与拟合流量-效率曲线基本贴合，曲率基本保持一致，贴合精度较高，能够反映不同速度下流量与效率的变化状况。

图3 压比拟合对照图

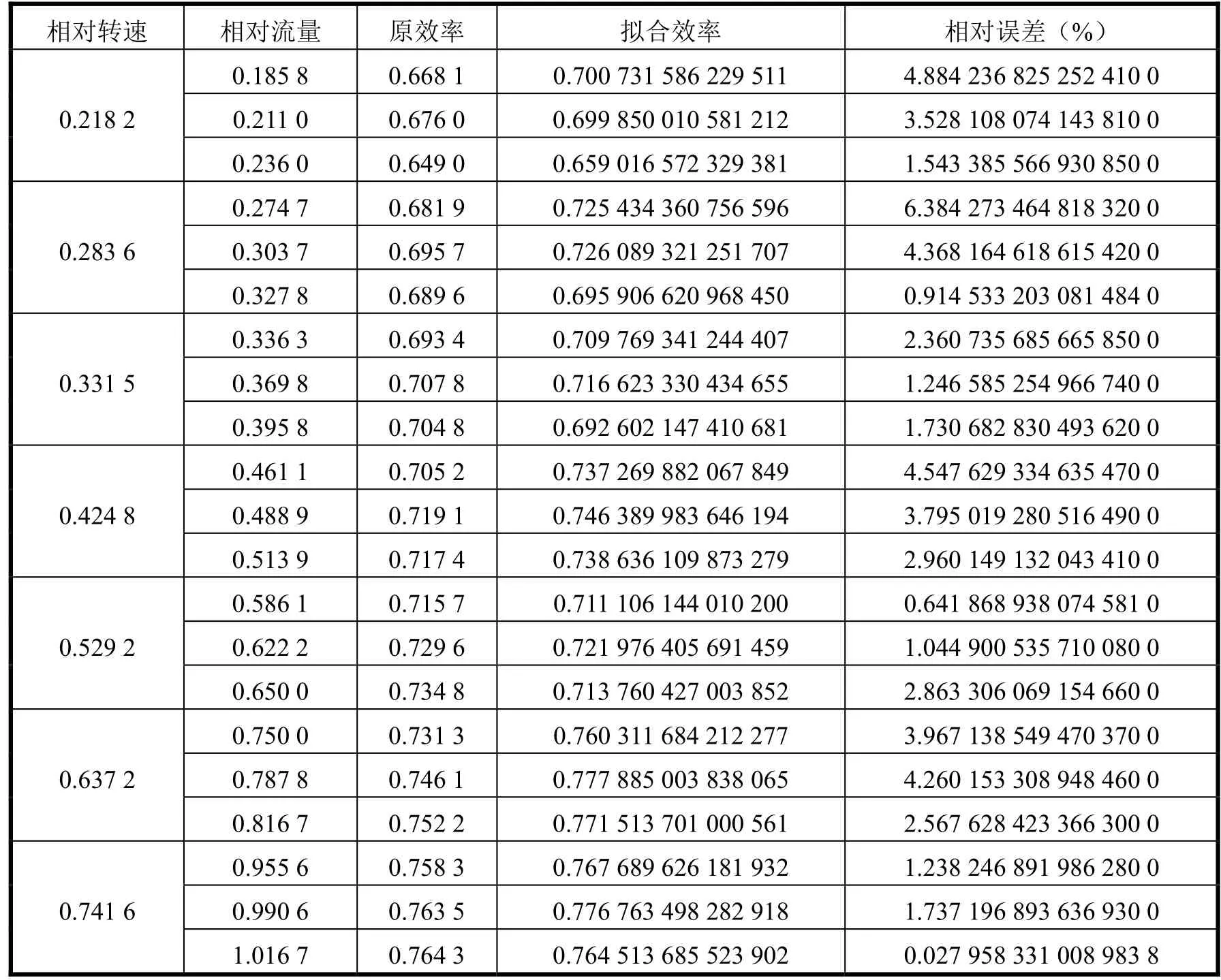
表4 效率拟合对照表

图4 效率拟合对照图

4 结论

本文研究的压气机特性曲线拟合方法原理简单、易于编程，拟合后的多项式可直接用于仿真程序，计算速度快、误差小，且符合精度要求。验证结果表明：该方法在拟合效果上是合理可行的，可为燃气轮机整机的仿真模拟提供坚实的基础。

[1] 徐海成.基于BP神经网络的涡轮增压机组压气机特性计算[J].计算机与数字工程, 2011, 39(6):18-20.

[2] 王志涛,李淑英,谭智勇. 基于BP和RBF神经网络压气机特性曲线拟合方法的研究[J]. 汽轮机技术,2009,51(2): 94-99.

[3] 彭靖波,谢寿生. 基于 RBF 神经网络的压气机特性仿真[J]. 推进技术,2006,27(1): 30-32.

[4] 赵雄飞,刘永葆,贺星,等. 基于统计学检验指标的燃气轮机部件特性方程拟合次数的选择[J]. 航空发动机,2011,37(5): 7-10.

[5] 杨欣毅,沈伟,刘海峰,等. 一种应用滑动最小二乘求取压气机特性的方法[J]. 航空动力学报,2009,24(8): 1741-1746.

[6] 刘喜超,唐胜利. 基于偏最小二乘法的压气机特性曲线的拟和[J]. 汽轮机技术,2006,48(5):327-329.

[7] 崔茂佩.压缩机特性线的系数拟合法[J].热能动力工程,1999,14(79): 43-46.

[8] 骆广琦, 桑增产. 航空燃气轮机涡轮发动机数值仿真[M]. 北京: 国防工业出版社,2007.