破解ex与lnx联姻题的四种策略

安徽省霍邱县第一中学

冯克永 (邮编：237400)

ex与lnx是高考考能力的经典载体，倍受命题者的青睐，每年高考至少出现一个.两者联姻产生的问题，更具有抽象程度高、求解灵活性大的特点，对解题者的数学技能及创新意识的考查具有独到之处.因而，它成了数学高考复习的难点和竞赛命题的热点.本文通过实例介绍四种常见的变通策略，供读者参考.

1 直接运算

对所给问题尝试对其进行一系列运算求解.

例1已知函数f(x)=xlnx-aex有两个极值点，求实数a的取值范围.

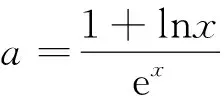
点评直接进行一系列求导运算，没有涉及较难的导数值等于0的求解问题，凸显解决此类问题的常规方法.

2 顺猜转化

直接运算难成功，尝试顺应命题者的意图猜，使其转化前行.

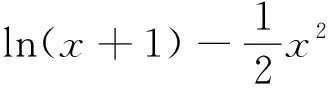
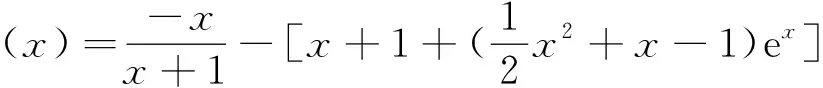
3 分而治之

直接运算很难进行，尝试将ex与lnx分开运算求解.

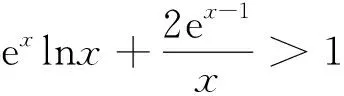
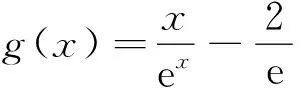
点评分开转化，分别求其最大值与最小值，走不等式证明的极端处理法(最小值大于最大值)，方法奇特，耐人寻味.

4 放缩转化

ex与lnx存在很难处理，尝试利用常见不等式(如ex≥x+1(x∈R,当且仅当x=0时等号成立)与lnx≤x-1(x>0,当且仅当x=1时等号成立))或题证不等式，将其放缩消失转化求解.

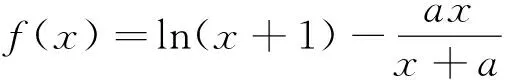
(1)当0≤a≤2,求函数f(x)的单调区间；

(2)证明：当x>0时，(ex-1)ln(x+1)+ex>x2+x+1.

解析第(1)问比较常规，第(2)问联想到不等式(1)处理.

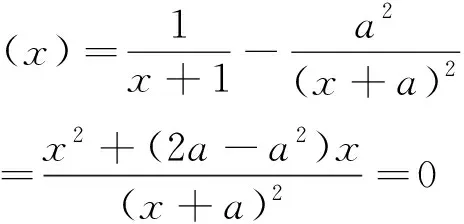
解得x=0或x=a2-2a,又0≤a≤2,所以a2-2a≤0,又x≥0,所以f′(x)≥0,所以函数f(x)的单调递增区间为[0,+∞).

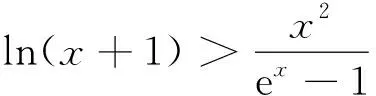
点评不等式是深刻认识函数的重要工具，二者结合是近几年高考命题的新热点.第(1)小题是常规的导数题易解决，第(2)小题利用常见不等式ex≥x+1及加法运算化整体为局部，再利用第(1)小题的结论，取a=2放缩传递是神来之笔，很值得回味.试题命制一般遵循设问之间的连贯性，在后问“山穷水尽”之时，前问(有时即使未解决，用其结论也可以)往往会带来“柳暗花明”之喜，这应引起我们的高度重视.

例5已知函数f(x)=xex-a(lnx+x).

(1)若函数f(x)恒有两个零点，求实数a的取值范围；

(2)若对∀x>0,恒有不等式f(x)>1成立.

①求实数a的值；

②证明：x2ex>(x+2)lnx+2sinx.

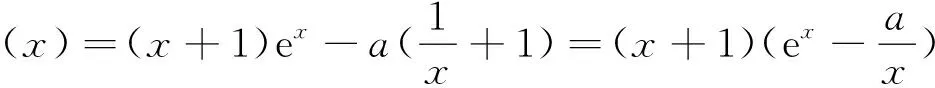
(2)①由(1)知，当a≤0时，f(x)在(0,+∞)上单调递增，f(x)的值域为R,不符合题意；当a>0时，f(x)max=a-alna,故只需a-alna≥1.令g(a)=a-alna,则g′(a)=-lna,所以g(a)在(0,1)上单调递增，在(1,+∞)上单调递减，从而g(a)max=g(1)=1,所以a-alna≤1,故满足条件的实数a=1.

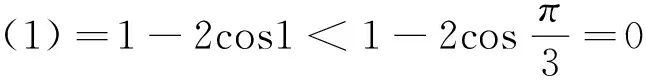
解法二由x2ex>(x+2)lnx+2sinx，得x2ex-(x+2)lnx-2sinx>0,再由x>0,ex>x+1,lnx≤x-1,sinx0,从而g(x)在(0,+∞)上的最小值为g(1)=13-3×1+2=0,所以x3-3x+2≥0,故x2ex>(x+2)lnx+2sinx.

点评第(1)问采用直接运算处理，对导数值等于零很难解时，常采用设而不求的处理策略，解法通性.第(2)题的第①题解法常规，目的是为第②题放缩服务的，加之常见不等式的参与，凸显命题者的意图及第②题解法一的美妙. 第②题的解法二摆脱第①题的安排，利用三个常见不等式同时放缩转化，思维奇异，越思越有味，越想越奇妙. 运用常见不等式放缩解决ex、lnx与sinx的联姻题往往能达到“鱼翔浅底、鹰击长空”的境界.方法思考的过程是痛苦的，解完后是快乐的，让人感悟数学的奇异与美妙.