力学选择题特殊解法示例
湖北省宜都市一中 谭 俊 罗 琼
物理选择题是高考试卷中很重要的一类题型,它既有单选题又有多选,它包含的知识点多,信息量大,灵活多变等特点。下面介绍一些做好选择题的特殊方法:
1.选项特征法
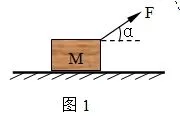
例1:如图1所示,位于水平面上的质量为M的小木块,大小为F、方向与水平面成α角的拉力下,沿地面做加速运动,若木块与地面之间的动摩擦因数为μ,则木块的加速度为
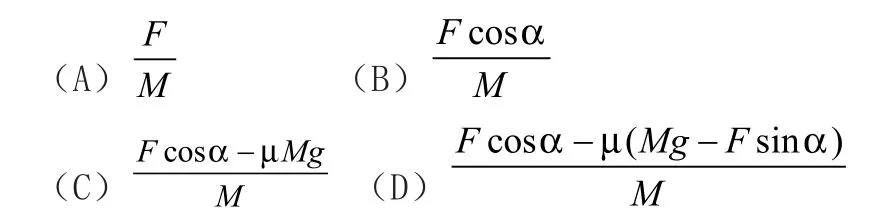
分析:由于M的加速度满足这一特征选项的只有D,故选D。
2.排除法
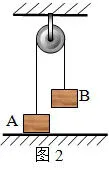
例2:两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止于水平地面上,如图2所示。不计摩擦,A对绳的作用力的大小与地面对A的作用力大小分别为
(A)mg ,(M-m)g
(B)mg ,Mg
(C)(M-m)g ,Mg
(D)(M+m)g ,(M-m)g
分析:由于A拉绳的力等于B拉绳的力等于mg,所以C、D错误。
又因为A受到绳子向上的拉力,地面对A的支持力小于Mg,所以B错。
故选A。
3.特殊取值法
例3:如图3所示,一根轻质弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体,质量为m。当盘静止时,弹簧的长度比其自然长度伸长了L。今向下拉盘使弹簧再伸长ΔL后停止。然后松手放开,设弹簧总处在弹性限度以内,则刚松开手时盘对物体的支持力等于
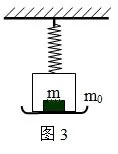
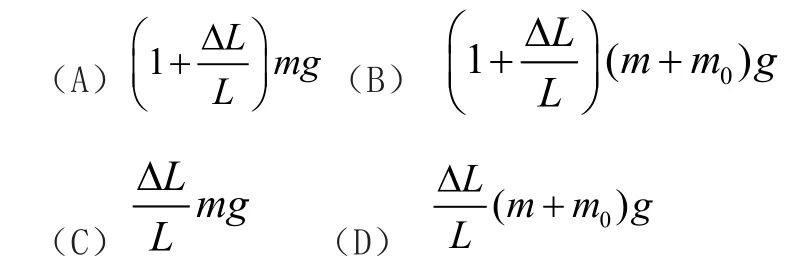
分析:取特殊值ΔL=0,此时盘和物体处于静止状态。盘对物体的支持力N=mg,附和这一答案的只有A,故A正确。
4.极限法
例4:两物体A和B,质量分别为m1和m2,互相接触且放在光滑的水平面上,如图4所示。对物体A施以水平推力F,则物体A对B的作用力等于
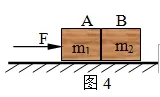
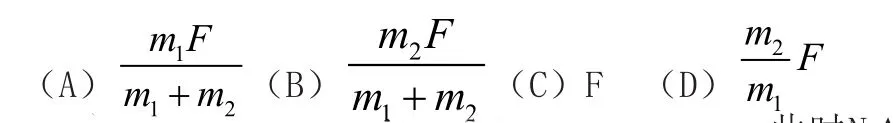
分析:当m1=0时,推力F将直接作用于m2,此时NA B=F。符合这一结果的只有B和C。又当m1→∞时,a→0,NAB→0,B、C中的B正确,故选B。
5.超重、失重法
例5:图5中的A为电磁铁,C为秤盘,A和C的总质量为M。B为铁片,质量为m。整个装置用轻绳悬挂于O点。当电磁铁通电,铁片被吸引上升的拉力F的大小为
(A)F=Mg
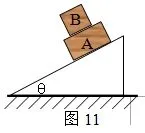
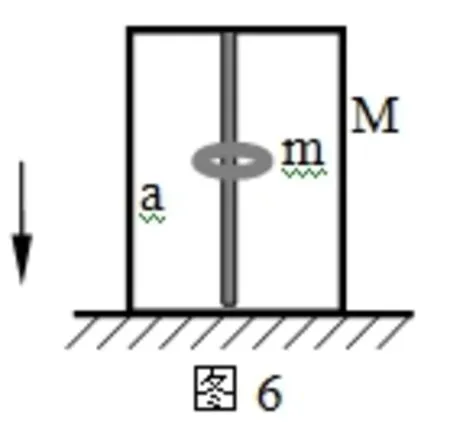
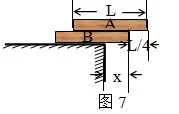
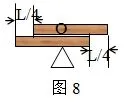
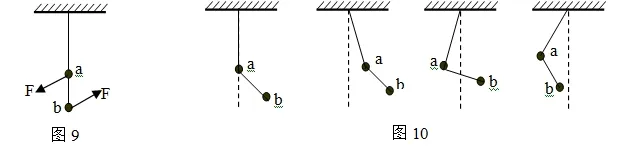
(B)Mg (C)F=(M+m)g (D)F>(M+m)g 分析:当电磁铁通电,铁片被吸引上升时,由于距离越近,引力越大,所以铁片变加速上升,处于·超重状态。故轻绳除负担Mg的重量外,还要负担比mg大的重量。故D正确。 例6:如图6所示,一个箱子放在水平面上,箱内有一固定的竖直杆。在杆上套有一个环。箱和杆的质量为M,环的质量为m。已知环沿着杆加速下滑,环与杆间的摩擦力大小为f,则此时箱对地面的压力为 (A)等于Mg (B)等于(M+m)g (C)等于Mg+ f (D)无法确定 分析:当f=0时,环以加速度g下降,环完全失重,箱对地面的压力为Mg。当f足够大时,环静止在杆上,环箱的重量全部压在地上,箱对地面压力为(M+m)g。因此Mg 例7:两个球形行星A和B各有一卫星a和b。卫星的圆轨道接近各行星的表面,如果两行星质量之比,两行星半径之比,则两卫星周期之比为 分析:由于,所以,故选项A正确。 例8:图7中,A、B是两块相同的均匀的长方形砖块,长为L,叠放在一起。A砖相对于B砖伸出L的长度。B砖放在水平桌面上且砖的端面与桌面平行,为保持两砖都不翻到,B砖伸出桌面的长度x的最大值是 分析:如图8所示,视A、B为一整体,是以O为中心对称图形,则桌边支在A、B的几何中心处时,A、B均不翻到且x最大,故故C正确。 例9:用轻质细线把两个质量未知的小球悬挂起来,如图9所示。今对小球a持续施加一个左偏下300角的恒力,并对小球b持续施加一个右偏上300角的同样大小的恒力,最后达到平衡。表示平衡状态的图可能是图10中的 分析:由于a上端的绳子负担着a、b整体的力,所以以a、b整体为研究对象,a、b整体在水平方向三合外力为0,所以整体不左右移动,上端的绳子不左右偏移,满足这一特征的图只有A,故选A。 例10:从地面竖直上抛一小球,设小球上升到最高点所用的时间为t1,下落到地面的时间为t2。若考虑空气的阻力作用,则 (A)t1> t2(B)t1< t2(C) t1=t2 (D)因不知速度和空气的阻力的关系,故无法确定t1、t2哪个大 分析:设上抛的初速度为v0,落地的速度为vt,则故B正确。 例11:两个重叠的滑块,置于固定的倾角为θ的斜面上,如图11所示。滑块A、B的质量分别为M和m,A与斜面间的摩擦系数为μ1,B与A间的摩擦系数为μ2,已知两滑块都从静止开始以相同的加速度沿斜面滑下,则B受到的摩擦力 (A)方向沿斜面向上 (B)方向沿斜面向下 (C)大小等于零 (D)大小等于μ1mgcosθ 分析:A、B一起沿斜面加速度下滑的真实加速度为a真=gsinθ-μ1gcosθ,若假设AB间无摩擦,则aB=gsinθ>a真。故B所受摩擦力沿斜面向上,A正确。 又对B有:mgsinθ- f=mBa真,即:mgsinθ- f=mB(gsinθ-μ1gcosθ), 故: f=μ1mgcosθ,故D正确。因此本题选A、D。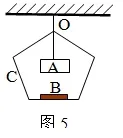
6.区间法
7.比例法
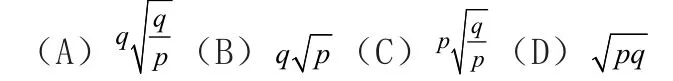
8.对称法

9.整体法
10.平均值法
11.假设法