《大不列颠的海岸线有多长》的内容及思想探析
江 南,曲安京
(1.西北大学 科学史高等研究院,陕西 西安 710127;2.西安石油大学 理学院,陕西 西安 710065)
1967年,一篇题为《大不列颠的海岸线有多长》[1]的划时代论文在权威期刊《Science》上发表,引起了数学家们极大的兴趣,它是20世纪几何学史上的又一次革命。作者是美籍法裔数学家芒德勃罗(B.B. Mandelbrot,1924—2010)。1924年,他出生在波兰华沙的一个犹太人家庭,家庭学术气氛浓厚,母亲是一位牙科医生,父亲是一名服装商人,叔叔芒德勃罗伊(S.Mandelbrojt, 1899—1983)是布尔巴基学派的一名数学家。芒德勃罗受叔叔的影响研究范围广泛,涉及数学、物理学和经济学等领域,但他最大的成就则是创立了分形几何。1975年,他用法文出版了第一本分形专著——《分形: 形式、机遇和维数》[2],第一次提出“分形”一词,系统地给出了分形的内容、思想和方法,标志着分形几何的诞生。随后他又发现了芒德勃罗集,用于描述复杂的、无穷无尽的分形形状。他一生获得了很多学术荣誉和头衔,其中包含著名的富兰克林奖章和沃尔夫物理学奖。沃尔夫奖委员会对他的评语是“通过认识分形普遍存在和发展研究分形的数学工具,他改变了我们的自然观。”
海岸线长度问题是一个地理测量问题,英国数学家里查逊(L.F.Richardson,1881—1953)考察了这一问题,发现西班牙、葡萄牙和比利时等国出版的百科全书中记录的一些海岸线长度竟相差20%,大大超过了允许的误差。为什么会产生如此大的误差呢?里查逊经过深入研究,认为这跟测量海岸线的“尺度”有很大的关系,当测量海岸线的“尺度”越来越小时,所测海岸线的长度则会越来越长。那么,海岸线的长度应当如何测量?选取什么样的“尺度”才能测得精确的海岸线长度?一般认为随着选取“尺度”的减小,所测海岸线长度的值可能会收敛到代表海岸线“真正长度”的有限数。 然而,里查逊已经证明事实并非如此[3],而是当测量“尺度”的长度越来越小时,海岸线的长度以及其他自然特征的增长是没有极限的。由于里查逊的研究主要集中在数学和物理方面,并且关于海岸线长度问题的研究在他死后才得以出版,所以这个研究被当时主流科学界所忽略,直到1967年,数学家芒德勃罗才敏锐地将这一研究引入他的《大不列颠的海岸线有多长》这篇划时代的论文,引起了科学界的重视。
数学思想始终是数学史研究所应关注的主题,在很大程度上,数学史就是数学思想史[4,P55]。那么《大不列颠的海岸线有多长》这篇论文所蕴含的数学思想是什么?这些思想将对分形几何产生什么样的影响?既然《大不列颠的海岸线有多长》如此重要,通过它作者试图解决什么问题?怎样解决这些问题?国内外对这方面的研究已有所涉及[5-12],如林夏水在《分形的哲学漫步》[11]中指出这篇论文提出海岸线长度随着量尺的不断缩小而趋向无穷大,对于传统的维数理论是一个巨大的挑战。本文将在这些研究的基础上对这上述问题进行深入探讨和系统分析。
1 《大不列颠的海岸线有多长》的内容及思想
对于《大不列颠的海岸线有多长》这个标题,没有读过该论文的人还会误认为作者的目的是去求大不列颠海岸线的长度,实际上大不列颠的海岸线有多长仅仅是论文的一个引子,而论文的主要内容却在副标题——统计自相似性和分数维数展现。按照内容的编排秩序,论文可以分为四部分。第一部分是1-3段,主要指出用长度来描述海岸线是没有意义的;第二部分为4-6段,主要介绍里查逊经验法则;第三部分是7-9段,主要是验证里查逊经验法则,并引出分数维数;第四部分为最后3段,主要是论述统计自相似性,提出尚待解决的问题。
1.1 海岸线长度
在第一部分,论文一开始就通过海岸线的形状来引出副标题所提及的统计自相似性定义:
“统计自相似性是指对于曲线的每一部分都可以认为是其整体统计意义上缩小的像,而描述海岸线形状的曲线正是与这类曲线密切相关的一个例子。”[1,P636]
定义结束后,芒德勃罗指出对于这样一些特殊形状的曲线用长度来描述通常是没有意义的。但是为什么会没有意义呢?他引用了施坦因豪斯(H.Steinhaus,1887—1972)在1954年的一个短评:
“随着测量精确度的提高,维斯瓦河左河畔的长度可以比从学校地图上读取的长度大10倍、100倍、甚至1000倍。”[13,P8]
在短评中,维斯瓦河左河畔的长度随着测量精度的不同而改变,自然将导致芒德勃罗对长度这个量客观存在性的怀疑。一般认为海岸线长度是一个是客观存在的数值,它为什么会随着测量精度的提高而增加呢?通过芒德勃罗的陈述,可知这与海岸线的复杂结构有关,那么海岸线的结构复杂程度又应该用什么来描述?在论文第二段,芒德勃罗指出描述一条地理曲线的复杂程度可以用一个量但不是长度来描述区分。如果曲线是自相似时,它可以通过相似指数D来刻画,这个相似指数拥有维数的许多性质,对于曲线来说,这个指数通常是比1大的分数。紧接着,芒德勃罗在第三段指出在研究地质统计学、经济学和物理学等的机会现象问题中,自相似方法是一个有效的工具。事实上,许多噪音的维数包含在0和1之间,因此数学家将维数考虑为零到无穷之间连续的数。
1.2 里查逊经验法则
在第二部分,为了能更好地引入分数维数,芒德勃罗首先回顾了曾经试图用来测量海岸线长度的方法。他写到:
“因为微小的细节对地形几乎没有影响,可以选取正标度G作为地理意义上特征长度的下限,并在内陆上作一条最短的曲线来连接AB,这条曲线和大海之间保持一个距离G,然后估计海岸线上A和B点之间的长度。另外,可以用一些长度不超过G的直线段来绘制这条最短的曲线,这些直线段的顶点都在包含有A和B点的海岸线上。”[1,P636]
实际上,对于这个曾经试图用来测量海岸线长度的方法还有一些别的释义,海岸线的长度也可以通过移动地图上两脚规来测量,在G足够小的情况下,利用移动两脚规来数出顶点在曲线上边长为G的开放等边多边形(依据测量情况所确定的不封闭等边多变形)的边数,便能计算出海岸线的长度L(G)。然而不幸的是,地理学者们在G值的选取上存在很大的分歧,而L(G)的值在很大程度上取决于G的值。那么这个问题应当怎样解决呢?芒德勃罗在第五段分析到:
“了解由不同的G所确定的L(G)的值是有必要的,更好的是需要在L(G)和G之间建立一个分析规则。里查逊提出了一个完全根据经验特征的法则:L(G)=MG1-D,遗憾是没有引起人的注意。这里M是一个正常数,D至少是一个等于单位1的常数,这个边界特征D可能会使一个人对不规则边界的视觉感知产生积极的联系。”[1,P636]
根据这个经验法则,当D=1时,地图上的边界看起来应该是笔直的;世界上最不规则的大不列颠西海岸线的特征D=1.25;德国陆地边界线的特征D=1.15;西班牙和葡萄牙边界线的特征D=1.14;地图集中最光滑的海岸线之一的南非海岸线的特征D=1.02。然而这些边界线与普通的光滑曲线有着显著的区别,因为光滑曲线可以通过长度来进行描述,并称为是“可求长的。”换句话说,里查逊所描述的那些边界线则是“不可求长的。”如同施坦因豪斯在1954年的短评中叙述道:
“如果认为自然中所遇到的大部分的弧都是不可求长的,那么我们就是在接近真实的情况。这个结论与不可求长的弧是数学家创造出来的以及大自然的弧都是可求长的这一信念相反,而这个相反的结论是正确的。”[13,P8]
论文标题所提出的问题实际上在此就能作出回答,大不列颠海岸线的长度是随着测量精度的增加而不断增长的(直至无限)。
1.3 分数维数
在第三部分,芒德勃罗一开篇就指出第二部分中引用里查逊经验法则的目的是为了反对曲线的维数大于1是由数学家发明的观点。但是实际问题出现后,数学家们一般是不会袖手旁观的,况且维数还是数学中一个非常重要的概念。那么维数概念最原始的特征是什么?分数维数在数学中又是怎样推导出来的呢?芒德勃罗分析到:

那么以此类推,当N1/D是一个正整数时,一个D维形体就可以被分割为N个与它的相似比率为r(N)=1/N1/D的更小D维形体。因此,此时的维数D可以通过D=-logN/logr(N)这样的对数关系式来表示。通过以上分析,我们知道维数D可以用来表征更一般的复杂形体。只要这个形体可以精确地分割为N个与整体相似比为r(N)的小形体,那么它的维数就满足D=-logN/logr(N)的关系式。为了证明这样的形体存在,芒德勃罗详细展示一些变异的连续不可微的科赫曲线的构造。具体构造如下:第一步,首先画一条(0,1)线段,长度为1;第二步,在第一步的基础上,画一些如图1所示的扭结曲线段,每条曲线段均由N个首尾相接的长度为1/4的区间组成。第三步,用第二步所选取曲线段比率为r(N)=1/4的曲线段来替代第二步中每一个小的曲线段(共N个),得到N2个首尾相接的长度为1/16的区间。按此类推,当无限重复上述步骤时,可以得到一条自相似的连续多结的曲线。因为这条曲线也可以精确地分割为N个与整体相似比为r(N)=1/4的曲线段,那么这条曲线的维数D=-logN/logr(N)=logN/log4。芒德勃罗为什么要选取变异的科赫曲线作为例子?变异的科赫曲线到底有什么特别之处?通过它的构造不难发现它与海岸线有很多相似的地方,或者从某种程度上说它就是一条特殊的海岸线。它的近似长度又应当怎样来测量呢?根据上述曲线的构造可知在第s+1步时,曲线由Ns个长度为G=(1/4)s的线段构成,所以此时曲线的近似长度L=(N/4)s=G1-D。细心的读者一定会发现这个关系式实际上就是里查逊经验特征法则中常数M=1的情形。
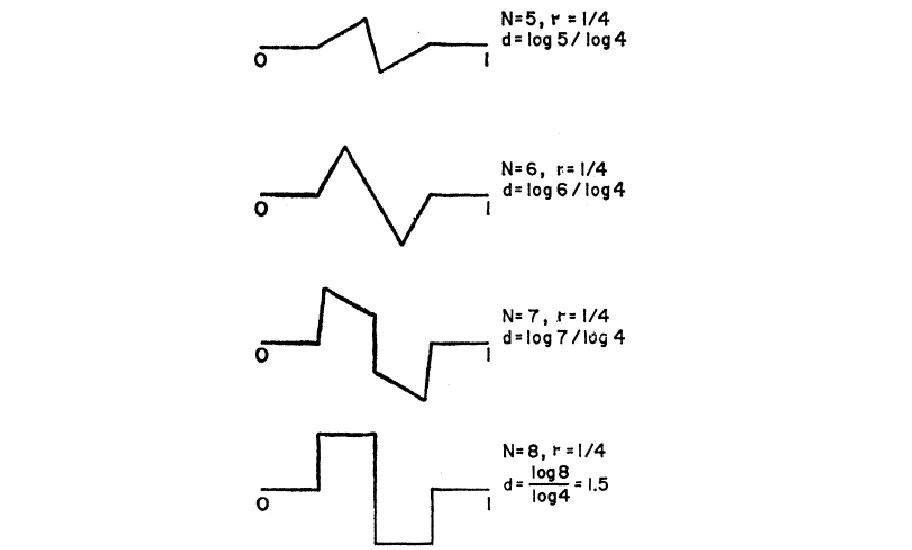
图1 扭结曲线段[1,P637]Fig.1 Kinked curves
1.4 统计自相似性
在后3段中,论文指出自相似图形在大自然界中也是很少见的,而统计意义上的自相似性图形却经常碰到,而要把这个问题描述清楚就需要引入概率、随机性以及相似维数等一些数学概念。正如芒德勃罗在第十段写到:
“一个平面图形的随机选择隐含着几种定义。首先必须先选取出一族可能的形状,通常用Ω来表示。当这族图形包含有限个成员时,随机选择的规则是通过每一个图形可能被选取的明确概率来指定。然而,当Ω在无限的情况下每一个图形被选取的概率是0。”[1,P637]
如果要求是自相似的,对于上述族Ω与事件的定义和概率一起需要满足两个条件:第一是每一个可能的图形必须通过N个与其相似比是r的小图形以某种方式的串接来构造;第二是概率应该特别指定,不管是一下子选取整个图形,还是分别选取小图形所得到概率值都一样。这样如果r的值是通过选取N来指定,那么可以将-logN/logr考虑为该图形的一个相似维数。因为相似维数在当时是一个比较新的数学概念,所以芒德勃罗在文末也说道:
“为相似维数的存在规定数学条件是一个并没有完全解决的问题。”[1,P638]
事实上,从论文第三部分可以看出地理曲线的随机思想升华了一些其他随机应用领域的概念性问题。由于论文的写作灵感得益于里查逊的遗稿,所以芒德勃罗最后指出里查逊的经验法则是随机自相似的地理曲线和分数维数D思想兼容最完美的表现形式,再一次肯定了里查逊的开创性工作。
2 《大不列颠的海岸线有多长》对分形几何的影响
分形几何是继随机数学、模糊数学和浑沌学后,又一门研究事物连续非光滑规整形态的数学分支。用通俗的方法讲,它是研究自相似复杂图形和结构的几何学。自相似性和分数维是它的两个基本思想,分数维是刻画分形最关键的特征量。分形一般具有以下性质[14]:具有精细的结构,即在任意小尺度它总具有复杂的细节;太不规则,以至于它的整体和局部难以用传统欧氏几何的语言来描述;具有某种自相似性,可能是近似的或是统计的;它的分形维数(以某种方式定义)一般会大于拓扑维数;以非常简单的方法定义,可能由迭代来产生。
论文中芒德勃罗以统计自相似性和分数维数这两个分形几何学中的重要概念作为副标题,接着通过对海岸线及地理曲线的研究引进第一类分形,即维数大于1的连通曲线。在逐阶计算变异的科赫曲线的近似长度时,惊讶的发现近似长度值的解析式是里查逊关于海岸线的经验法则的解析式L(G)=MG1-D中M=1的情形。主要区别是这里D不再是一个要通过经验估计的物理量,而是一个数学常数,通过它可以定义相似维数,即分形维数的一种新的表达方式。正如芒德勃罗回忆时说:
“解释1-D是我在此领域的第一个贡献,在《大不列颠的海岸线有多长》这篇论文中我挖掘出了里查逊可能被永远埋没的论文,并将D解释为分形维数。”[2,P33]
事实上早在1918年,豪斯多夫(F.Hausdorff,1868—1942)在他的《维数和外测度》这篇论文中已经对分数维数有详细的研究[15],不过当时是纯数学的角度来引出分数维数,还未在大自然中找到与之相对应的实体。而在《大不列颠的海岸线有多长》这篇论文中,芒德勃罗以海岸线问题为突破口,在大自然中实现了维数由整数到分数的飞跃,因而分形几何又称为大自然中的几何。论文还介绍了与大自然密切相关的统计自相似性,为1982年出版的分形名著——《大自然的分形几何》[5]提供了重要素材,也为第一部分形著作——《分形、机遇和维数》的出版作出了铺垫,进而为分形几何的最终诞生奠定了基础。通观全文,无处不渗透着分形的思想,它的发表标志着分形理论的萌芽。
3 结 语
海岸线长度问题是芒德勃罗最初在里查逊遗稿中的一篇鲜为人知的论文中发现的问题,这个问题引起了他极大的兴趣,并进行了潜心的研究,《大不列颠的海岸线有多长》就是他的研究成果之一。海岸线长度的测量取决于测量海岸线尺子的精度,经验证据表明测量的尺度越精细,测出的海岸线就越长。当测量的尺度趋于零时,海岸线的长度将趋于无穷。里查逊通过观察发现许多国家边界线测量出来的长度L(G)是测量尺度G的一个函数,并搜集了几个不同的例子,然后猜想出L(G)可以通过以下形式的一个函数来估计:L(G)=MG1-D。解释这个关系式中字母“D”的含义正是《大不列颠的海岸线有多长》需要解决的问题。芒德勃罗用数学建模的方式,通过类比的方法,最终证明了海岸线的近似长度确为L(G)=MG1-D中M=1的情形,并且将D解释为相似维数,并给出了计算相似维数的办法。
在论文接近尾声时,芒德勃罗论述了大自然中的统计自相似性,指出里查逊的经验法则是随机自相似的地理曲线和分数维数D思想兼容最完美的表现形式。这篇论文既显示了芒德勃罗早期的分形思想,同时又是数学与大自然紧密联系的一个例子。但因为分形几何的建立还需要一套系统的理论来支撑,而论文涉及的只是其中的一个方面,并且论文中芒德勃罗没有将相似维数明确为分形维数,也未抽象出“分形”这一概念,所以本篇论文不能作为分形几何诞生的标志。同时论文也提出了一些尚待解决的问题。如相似维数存在的严格数学条件是什么?里查逊经验法则中常数M的值如何来确定?这些问题自然也成了芒德勃罗以后工作的主题。
致谢:衷心感谢南京农业大学惠富平教授在本文写作过程中的悉心指导。
参考文献:
[1] MANDELBROT B B.How long is the coast of Britain[J]. Science,1967,156(3775):636-638.
[2] MANDELBROT B B. Les Objets Fractals:Forme, Hasard et Dimension[M]. Paris:Flammarion,1975.
[3] RICHARDSON L F.The problem of contiguity: An appendix of statistics of deadly quarrels[J]. General Systems Yearbook,1961,6(13):139-187.
[4] 曲安京.中国数学史研究范式的转换[J].中国科技史杂志,2005,26(1):50-58.
[5] MANDELBROT B B.The fractal geometry of nature[M]. New York: W H Freeman,1982.
[6] 李文林.数学史概论[M].北京:高等教育出版社,2002.
[7] 李润珍,武杰.分形几何的创立与复杂性研究[J].自然辩证法研究,2014,30(7):89-95.
[8] 刘华杰.分形之父芒德勃罗[J].自然辨证法通讯1998,20(1):54-64.
[9] 汪富泉,李后强.分形:大自然的艺术构造[M].济南:山东教育出版社,1996.
[10] 文志英,井竹君.分形几何和分形维数简介[J].数学实践和认识,1995,25(4):20-29.
[11] 林夏水.分形的哲学漫步[M].北京:首都师范大学出版社,1999.
[12] 孙博文.维数的性质及哲学意义[J].自然辩证法研究,1994,10(11):34-37.
[13] STEINHAUS H.Length, shape and area[C].Colloquium Mathematicum,1954,1(3):1-13.
[14] 沙震,阮火军.分形与拟合[M].杭州:浙江大学出版社,2005.
[15] HAUSDORFF F. Dimension und äußeres Maß[J].Mathematiche Annalen,1918,79(1-2):157-179.

