H2+分子阈下谐波极化起源的理论研究

于术娟，董福龙，辛国国

(1.陕西师范大学 物理学与信息技术学院，陕西 西安 710119；2.西北大学 物理学院，陕西 西安 710069)

由于高次谐波的产生在阿秒科学中有重要的应用,近年来,越来越多的科研人员对其开始关注,在强场物理研究中成为热点研究问题[1-3]。其产生过程的简单物理图像可通过经典三步模型[4]描绘,即:①电子首先从库仑势和激光场形成的势垒中隧穿电离出去;②此时电子的行为更像一个经典的粒子被激光场加速;③当激光场改变其振荡方向时,自由电子的加速度发生反转并返回到核,最后落入初始束缚态与母核再结合并辐射出高能光子ω。这个过程被称为高次谐波的产生。但这个模型只能成功地描述阈上高次谐波(光子能量ω大于或者接近系统电离能Ip)的主要特性。以前人们的研究重点是高次谐波的域上部分，然而,在实验和数值模拟中,人们将光子能量ω低于电离能Ip时所对应的谐波称为阈下谐波，但是人们对阈下谐波的研究相对较少。近年来,被视为真空紫外线辐射潜在来源[5-6]的近阈和阈下谐波[6-14]引起了人们的广泛关注。在低能区域,由于忽略了库仑势和原子分子的电子结构,传统的三步模型和强场近似变得不充分了。已有研究表明,在对近阈谐波的贡献机制上,长短电子轨道是不同的,而且被考虑库伦效应和激发效应的发展三步模型所描述[8-9]。除了量子轨道外,激发态对阈下谐波的产生也有显著影响[5,11,15-18],最近已经在实验上展示过了[10]。

以前人们只关注阈下谐波功率谱的研究。目前,对称分子阈下谐波的极化性质引起了人们极大的注意。阈下谐波的极化因为取向效应的原因导致其既与平行谐波相关,也和垂直谐波相关。已有对阈下谐波极化性质的研究结果表明,阈下谐波极化的产生机制不同于阈上谐波,不同能量区域的阈下谐波的极化有不同的产生机制。在较低阶阈下谐波的情况下,分子较高极化的起源是基态和几个能量较低的激发态之间的共振效应。然而,较高阶阈下谐波极化的复杂起源却几乎没有被研究过。

本文通过求解含时薛定谔方程的方法详细地研究了在不同取向角及不同激光波长的情况下对称分子H2+[19-20]的较高阶阈下谐波的极化。结果表明:激发态仅对较高阶阈下谐波的极化在较小角度的情况下有影响;此外,通过对精确计算得到的谐波和只有短轨道贡献的谐波的比较,预示了较高阶阈下谐波的极化也受长短电子轨道之间的干涉的影响。

1 数值方法

(1)

其中，ψ(t)是对应含时哈密顿H(t)的含时波函数。依照强场近似[22]理论,仅考虑电子与基态再结合对谐波辐射谱的贡献，

(2)

其中，a0(t)=〈0|ψ(t)〉。另外,高次谐波的极化率为

(3)

μ=S⊥/S‖是垂直和平行谐波的强度比,δ=φ⊥-φ‖是相位差。这里S‖(⊥)=|F‖(⊥)(ω)|2和φ‖(⊥)(ω)=arg[F‖(⊥)(ω)],极化的范围是0≤ε≤1,从式(3)可以看出,当平行和垂直谐波的强度差不多且相位差δ为π/2时，高的极化就显示出来。

2 数值结果和讨论

2.1 不同能量区域极化的产生机制

文献[23]指出,对于较低阶的阈下谐波,高的谐波极化与基态和激发态的共振效应密切相关;而对于较高阶阈下谐波,高的谐波极化的产生机制并没有被讨论过。本文将讨论上述现象背后的物理机制，为了对照,平台区域的谐波极化同时也被讨论。

已有研究表明,在返回过程中,激发态在两中心干涉的特殊区域对于谐波的释放起到重要的作用。依照激发态对不同能量区域谐波极化的影响,将不同能量区域分为较低阶谐波和较高阶谐波,如图1所示，其中激光强度I=5×1014W/cm2,θ=20°。图1(a)和图1(b)分别呈现了λ=400nm的平行和垂直谐波辐射谱强度，图1(d)和图1(e)呈现了λ=760nm的平行和垂直谐波辐射谱强度。其中，方块曲线是通过式(1)计算得到的精确谐波，圆圈曲线是通过式(2)计算得到的。对于图1中λ=400nm的情况,圆圈曲线在较低阶的谐波(图1中用虚线箭头表示的低于第七阶的谐波)与通过精确计算得到的谐波(方块描述)符合的很好。低于第七阶的谐波被定义为较低阶阈下的谐波区域,在这个区域里只考虑跃迁到基态的谐波在谐波释放中起主要作用。对于高于第七阶的较高阶谐波,在图1(a)中的圆圈曲线上观察到一个显著的凹陷,而在通过精确计算得到的方块曲线上没有观察到这个凹陷，这个现象预示了激发态在这个区域起主要作用。相应地,

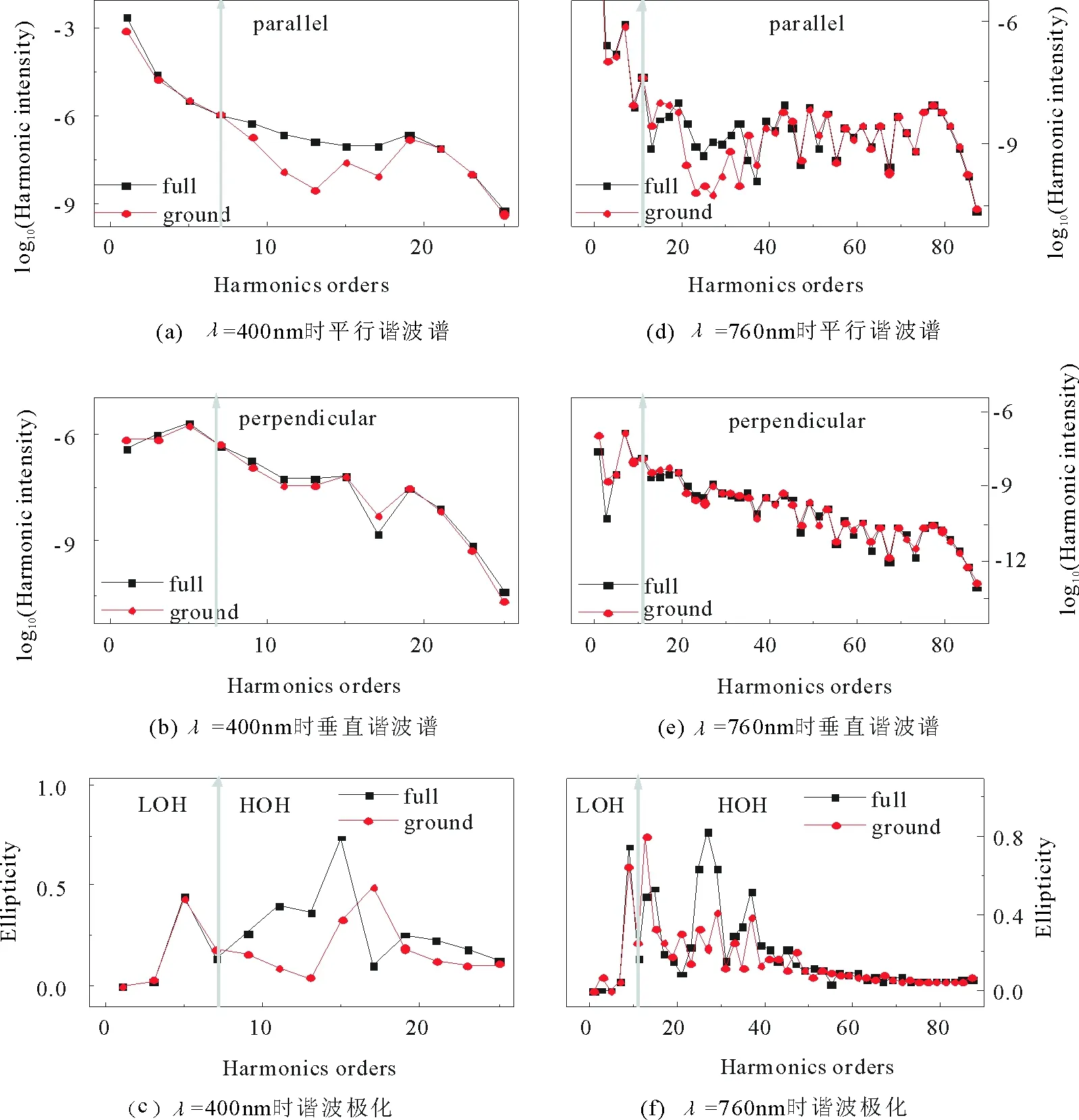
图1 θ=20°时，精确计算的和只考虑基态贡献的平行、垂直谐波谱和谐波极化Fig.1 The parallel,perpendicular spectra and the ellipticity of harmonicsof full simulations and only considering the transition back to the ground state when θ=20°

通过精确计算得到的谐波的极化明显高于只跃迁到基态的谐波极化,如图1(c)所示。对于较长激光波长的情况,如图1(d)～(f)所示,观察到的现象跟图1(a)～(c)是相似的。在图1(b)和1(e)中,对于所有激光波长的情况,我们注意到激发态在垂直谐波辐射谱上基本不起作用。因此,在较高谐波阶时,在图1(c)和1(f)中观察到，通过精确计算得到的方块曲线显示出较高的极化。因此，总结出这个现象起源于返回电子与激发态再结合的贡献。

为研究观测角度对谐波极化的影响,与图1类似,图2给出θ=80°的大角度情况,圆圈曲线和方块曲线的谐波辐射谱对于所有波长的情况是相近的。因此,我们认为激发态在这个角度不起作用,而图2(f)中在21阶周围出现的高的极化起源于其他机制。接下来将探讨在21阶周围出现高的极化的起源。

2.2 较高阶阈下谐波极化的产生机制

基于以上讨论,对于较高阶阈下谐波,我们已经证明了跃迁到激发态的谐波对较高阶谐波的极化有重要影响。在对较高阶谐波极化的影响上,除了激发态的影响,长的量子轨道也有重要的作用。在图3和图4中，展示了激光强度I=5×1014W/cm2，波长为λ=760nm，θ为20°和80°时，分别通过精确计算(方块描述)和只考虑短轨道贡献(圆圈描述)得到的平行和垂直谐波谱。 通过精确计算得到的谐波与只考虑短轨道贡献的谐波相比是显著不同的, 这种不同对于图3和图4中所有谐波和极化的情况都是支持的。尤其是图4(c)中通过精确计算得到的结果(方块描述)在第21阶周围显示出较高的极化,而对应的短轨道的结果(圆圈描述)基本没有显示高的极化。这些现象意味着在角θ=80°时出现的高的极化起源于长短电子轨道之间的干涉。这些现象不同于图1和图2所展现出来的结果,在图1和图2中激发态仅对较小角度的较高阶阈下谐波起作用。

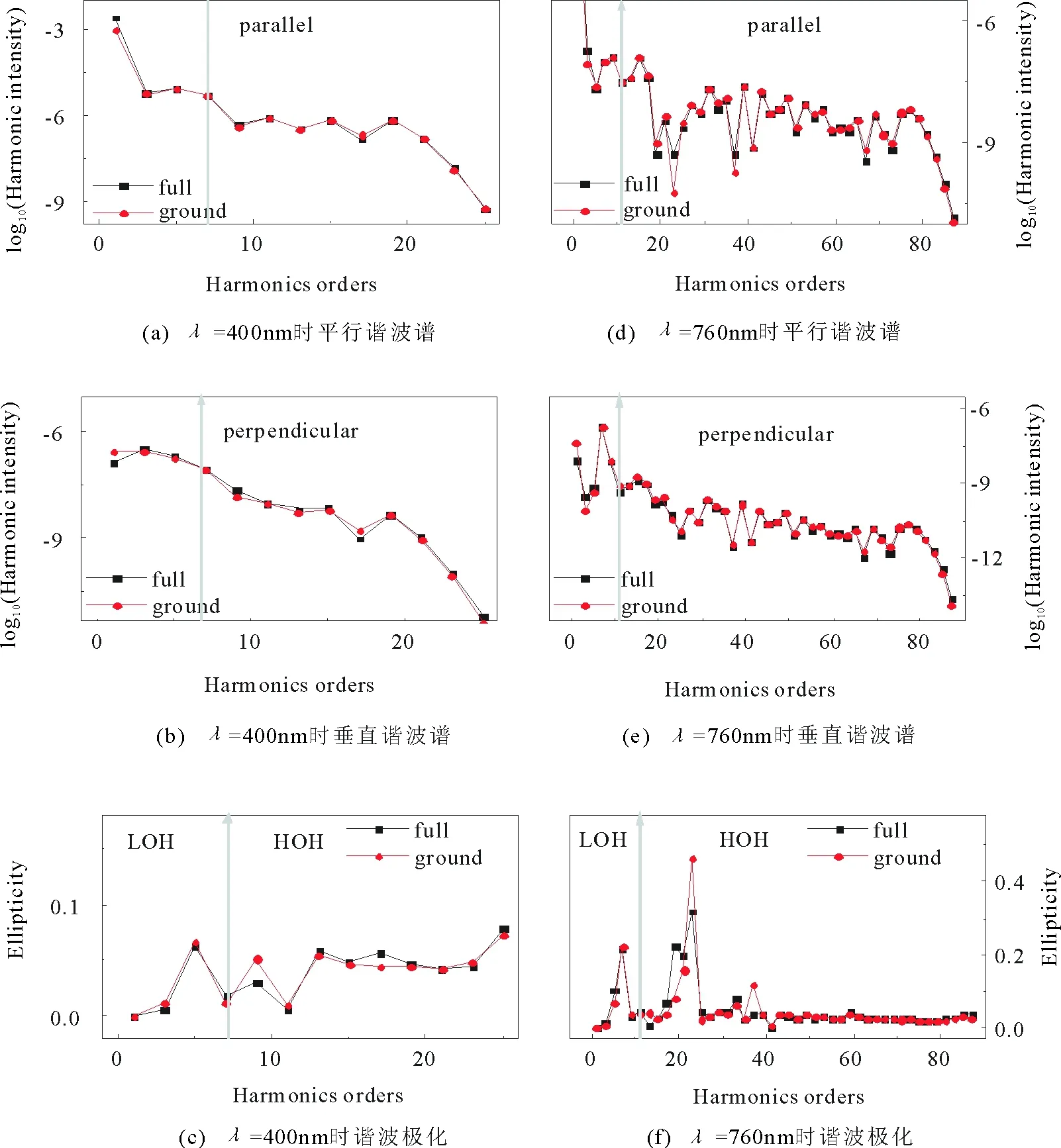
图2 θ=80°时，精确计算的和只考虑基态贡献的平行、垂直谐波谱和谐波极化Fig.2 The parallel,perpendicular spectra and the ellipticity of harmonicsof full simulations and only considering the transition back to the ground state when θ=80°

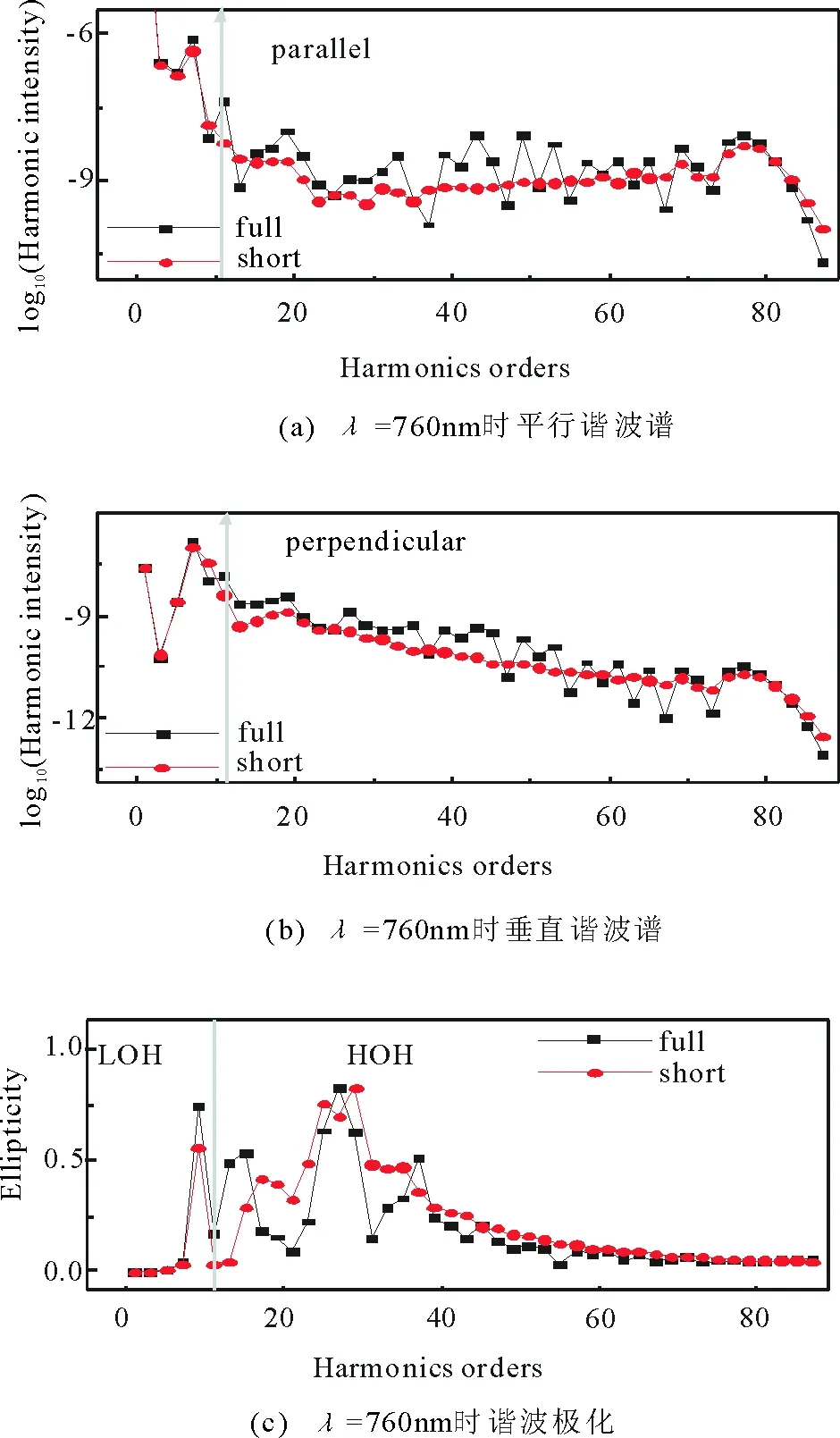
图3 θ=20°时精确计算的和只考虑短轨道贡献的平行、垂直谐波谱和谐波极化Fig.3 The parallel,perpendicular spectra and the ellipticity ofharmonicsof full simulations andonly considering the contributions of short trajectories when θ=20°

图4 θ=80°时精确计算的和只考虑短轨道贡献的平行、垂直谐波谱和谐波极化Fig.4 The parallel,perpendicular spectra and the ellipticity ofharmonicsof full simulations andonly considering the contributions of short trajectories when θ=80°

3 结 论

总之,本文详细研究了激发态及长短电子轨道对线极化强激光场中对称分子H2+较高阶阈下谐波的极化的影响。通过分析发现，阈下谐波极化起源于不同的机制。首先, 对于较高阶阈下谐波,通过精确计算得到的高的极化一部分起源于返回电子与激发态再结合的贡献。其次,较高阶阈下谐波的极化也受长短电子轨道之间干涉的影响。这些结果意味着阈下谐波的极化有复杂的起源。本文对阈下谐波极化的复杂起源的研究,是对过去的研究工作的补充。

参考文献：

[1] HUILLIER LA, SCHAFER K J, KULANDER K C. Theoretical aspects of intense field harmonic generation[J].Journal of Physics B: Atomic, Molecular and Optical Physics,1991, 24(15): 3315-3341.

[2] ITATANI J, LEVESQUE J, ZEIDLER D, et al. Tomographic imaging of molecular orbitals[J].Nature, 2004, 432(7019): 867-871.

[3] KRAUSZ F, IVANOV M. Attosecond physics[J].Reviews of Modern Physics, 2009, 81(1): 163-234.

[4] CORKUM P B. Plasma perspective on strong field multiphoton ionization[J].Physical Review Letters, 1993, 71(13): 1994-1997.

[5] HENKEL J, WITTING T, FABRIS D, et al. Prediction of attosecond light pulses in the VUV range in a high-order-harmonic-generation regime[J].Physical Review A, 2013, 87(4): 043818.

[6] YOST D C, SCHIBLI T R, YE J, et al. Vacuum-ultraviolet frequency combs from below-threshold harmonics[J].Nature Physics, 2009, 5(11): 815-820.

[7] POWER E P, MARCH A M, CATOIRE F, et al.Xfrogphase measurement of threshold harmonics in akeldysh-scaled system[J].Nature Photonics, 2010, 4(6): 352-356.

[8] HOSTETTER J A, TATE J L, SCHAFER K J, et al. Semiclassical approaches to below-threshold harmonics[J].Physical Review A, 2010, 82(2): 023401.

[9] SOIFER H, BOTHERON P, SHAFIR D, et al. Near-threshold high-order harmonic spectroscopy with aligned molecules[J].Physical Review Letters, 2010, 105(14): 143904.

[10] CHINI M, WANG X, CHENG Y, et al. Coherent phase-matched VUV generation by field-controlled bound states[J].Nature Photonics, 2014, 8(6): 437-441.

[11] XIONG W H, GENG J W, TANG J Y, et al. Mechanisms of below-threshold harmonic generation in atoms[J].Physical Review Letters, 2014, 112(23): 233001.

[12] BRIZUELA F, HEYL C M, RUDAWSKI P, et al. Efficient high-order harmonic generation boosted by below-threshold harmonics[J].Scientific Reports, 2013, 3: 1410.

[13] SHAFIR D, FABRE B, HIGUET J, et al. Role of the ionic potential in high harmonic generation[J].Physical Review Letters, 2012, 108(20): 203001.

[14] KATO K, MINEMOTO S, SAKAI H, et al. Phase differences of near-threshold high-order harmonics generated in atoms and molecules [J].Physical Review A, 2014, 90(6): 063403.

[15] BAKER S, ROBINSON J S, HAWORTH C A, et al. Probing proton dynamics in molecules on an attosecond time scale[J].Science, 2006, 312: 424.

[16] NABEKAWA Y, FURUKAWA Y, OKINO T, et al. Sub-10-fs control of dissociation pathways in the hydrogen molecular ion with a few-pulse attosecond pulse train[J].Nature Communications, 2016, 7: 12835.

[17] HESLAR J, TELNOV D A, CHU S I. Enhancement of VUV and EUV generation by field-controlled resonance structures of diatomic molecules[J].Physical Review A, 2016, 93(6): 063401.

[19] CHEN Y J, LIU J, HU B. Intensity dependence of intramolecular interference from a full quantum analysis of high-order harmonic generation[J].Physical Review A, 2009, 79(3): 033405.

[20] HAN Y C, MADSEN L B. Minimum in the high-order harmonic generation spectrum from molecules: Role of excited states[J].Journal of Physics B: Atomic, Molecular and Optical Physics, 2010, 43(22): 225601.

[21] FEIT M D, FLECK J A, STEIGER A. Solution of the Schrödinger equation by a spectral method[J].Journal of Computational Physics, 1982, 47(3): 412-433.

[22] LEWENSTEIN M, KULANDER K C, SCHAFER K J, et al. Rings in above-threshold ionization: A quasiclassical analysis[J].Physical Review A, 1995, 51(2): 1495-1507.

[23] DONG F L, TIAN Y Q, YU S J, et al. Polarization properties of below-threshold harmonics from aligned molecules in linearly polarized laser fields[J].Optics Express, 2015, 23(14): 18106-18116.