高频制动尖叫的振动能量流动分析∗

高 普，杜永昌，周 晗

(1.北京理工大学机械与车辆学院，北京 100081； 2.清华大学，汽车安全与节能国家重点实验室，北京 100084)

前言

车辆制动时动能通过摩擦副间的相对滑动作用转化为热能耗散，如果制动器设计不合理、摩擦材料老化或制动工况的改变，制动时就可能引起强烈的振动，并伴随着噪声。制动噪声是城市噪声污染源之一，且影响乘车舒适性，持续的振动还会影响车辆相关部件的疲劳寿命。因此，采取有效的措施对制动噪声进行控制十分必要[1－2]。

关于制动噪声的研究，最根本的是其产生的机理，这方面在国际上尚未达成共识。由于从不同产生机理出发，形成多种多样的分析手段和噪声抑制措施。

文献[3]和文献[4]中从摩擦副入手，认为摩擦副的本身的特性是引起制动振动噪声的根本原因。文献[5]中提到Sprag-Slip现象来解释制动噪声的形成。文献[6]中将盘式制动器制动片与制动盘之间的摩擦耦合作为非对角项引入系统刚度矩阵，以其不稳定复特征根表征系统振动的发散，引发振动噪声。文献[7]中在对鼓式制动器试验分析的基础上提出制动器结构的摩擦闭环耦合模型，认为摩擦力的引入导致系统刚度矩阵不对称，由于制动系统结构参数匹配不当，最后解得复特征值表征系统阻尼项的实部为正，即为产生制动噪声的原因。文献[8]中利用试验与仿真相结合方法，建立了鼓式制动器结构闭环耦合模型。文献[9]中认为制动噪声是由摩擦耦合诱发，系统各部件结构参数匹配不当导致的自激振动。文献[10]中也相似地认为，制动系统中，摩擦力激发了制动块与制动盘之间的切向和纵向共振，并导致制动块上压力波动；其波动加剧了块与盘之间的摩擦力变化，导致系统振动发散，尖叫产生。文献[11]和文献[14]中利用有限元及模态综合法建立了盘式制动器闭环耦合模型，并提出了子结构模态组成分析、子结构模态参数灵敏度分析等方法，有效地分析了结构参数对制动噪声产生的影响因素。

上述研究对制动噪声产生机理进行了较为全面的探究。高频尖叫频率范围为5～10kHz或到人耳听力的上限，由制动盘的面内和面外模态耦合产生，制动盘是影响制动器高频尖叫的关键子结构部件[15－17]。

建立制动器闭环耦合模型进行复特征值分析是一种行之有效的制动噪声频域分析方法[1]。以往闭环耦合噪声分析模型的不足在于:一是影响尖叫发生的子结构模态的频率和振型因素都很重要，仅从频率角度修改结构缺乏准确性；二是子结构贡献系数为复数，仅考虑幅值，不能全面表征子结构的动态特性。文献[18]中提出能量馈入的分析方法，该方法不仅考虑了尖叫模态的振幅，还涉及相位信息，分析角度更加全面；分析了馈入能量大小与尖叫倾向之间的对应关系，并以馈入能量大小作为指标，分析了摩擦副摩擦因数、制动块形状等参数对系统稳定性的影响。文献[14]中从能量馈入的角度出发，进行子结构模态参数的灵敏度分析，认为其具有与原有灵敏度分析结果的等价性，亦证明能量馈入法的实用性与可靠性。然而，对于馈入制动系统的振动能量在各子结构中的流动和传递路径尚未有相关的研究。本文中以此作为研究目标，推导子结构自身振动能量表达式和耦合界面间能量流动表达式，并进行能量平衡分析，得到振动能量流动传递路径，并从能量角度解释制动盘是制动高频尖叫产生的关键影响子结构。

本文中首先针对某一轿车浮钳盘制动器，建立制动噪声分析闭环耦合模型，进行复特征分析；推导制动盘自身振动能量表达式，并利用该式计算了13kHz的高频尖叫制动盘在静态和动态闭环耦合模型中自身振动能量；然后推导闭环耦合模型中制动块和制动盘界面能量流动表达式，分别计算该噪声频率的内外制动块与制动盘间振动能量流动，指出制动器在耦合界面的振动传递以制动盘振动向制动块传递为主导；最后通过制动盘振动能量平衡分析，证明制动盘振动能量计算的可靠性和准确性。并从能量角度，在机理层面解释了制动器高频尖叫产生的原因。

1 闭环耦合模型

图1为某浮钳盘式制动器三维有限元模型，其坐标系原点固定于制动盘中心，x轴正方向从坐标原点向上穿过制动缸的中心轴线，z轴正方向为水平向右，与制动盘轴线重合，y轴正方向按右手规则确定。

图1 制动器有限元模型

制动器可划分为5个子结构，以字母A～E代表，A为外制动片(outer pad)，B为制动盘(rotor/disc)，C为内制动片(inner pad)，D为制动钳(caliper housing)，E为制动支架(caliper bracket)。基于摩擦闭环耦合理论，建立钳盘式制动器各子结构(零部件)有限元模型，提取子结构模态参数，然后根据子结构间连接耦合关系，将独立的子结构进行模态综合，推导制动噪声闭环耦合模型。图2所示为各子结构耦合示意图。

在忽略了子结构本身的小阻尼的情况下，制动器的振动方程[11]为

图2 闭环耦合模型耦合示意图

式中:[M]为制动器有限元离散化后的质量阵，由各子结构的质量阵组合而成；[K]为制动器有限元离散化后的刚度阵，各子结构的刚度阵组合而成；u(t)为制动器有限元模型各子结构在物理坐标下，对应节点所组成的位移列向量；[Kf]为耦合刚度阵，[Kf]表示子结构之间的摩擦和弹性耦合，它由子结构部件之间的连接和相互作用关系确定。

式(1)表示的有限元模型阶数相当大，不利于求解。为解决上述问题，将物理坐标u(t)变换到各子结构模态的坐标{q}:

式中[Φ]为由各子结构对各自模态质量归一化的模态振型矩阵组合而成的矩阵。

经坐标转换后式(1)变为

其中

式中[Λ]为各子结构的模态角频率平方组成的对角阵。对式(3)进行复特征分析，可得到系统的复特征值和相应的特征向量。复特征值虚部表示噪声频率，实部代表模态阻尼。因此实部大于零的模态为负阻尼，对应系统中不稳定的、存在产生尖叫倾向的模态，称为噪声模态。噪声模态复特征值实部越大，说明发生噪声的倾向越大。

表1为某制动器得到不稳定模态。可以看出，13kHz噪声频率的实部最大，噪声倾向最大，可将13kHz频率的高频尖叫作为本文的算例。

表1 某制动器得到不稳定模态特征值

2 制动盘自身振动能量

在以往研究中发现，制动盘面内模态与面外模态发生耦合，形成不稳定模态，使系统趋于不稳定。振动能量在制动盘汇聚，制动盘的高速旋转会将高频振动辐射出去，带动周围空气波动，最终形成尖叫噪声，影响制动器的NVH性能。制动盘是制动器高频尖叫的关键子结构。

2.1 制动盘自身振动能量公式推导

在一个振动过程，势能与动能是相互转化的。在不考虑衰减的情况下，最大势能即为系统的总能量，而最大势能的计算可通过物理坐标下的最大响应位移推导出。

设l点第i阶的物理坐标的瞬态位移[19]为

式中:si和分别为共轭模态特征，可表示为σi＋jωi，σi－jωi；φli和为模态转化后第i阶l点相应的共轭模态振型，φli和分别为q0和为模态坐标初值，可表示为。 得到下式:

对式(6)运用欧拉公式:

式中r0取决于初始条件。由于模态综合模型建立的是一个发散的线性系统，发散项为eσit，在实际的系统中振动必然是收敛的，因此可以省略eσit，使振动更贴近实际情况[18]。另一方面，以最大势能表征系统的总能量，省略掉波动项 cos(ωit＋γi＋θi)。 最终得到物理坐标的瞬态位移为模态转化后第i阶l点相应的共轭模态振型的幅值φli。第i阶所有自由度的共轭模态振型可表示为

式中:[Φ]和[Φ∗]为模态综合前的振型，由于为实模态，故得[Φ]＝[Φ∗]；{ψi}和{}为模态综合方程的右特征向量，ψi和可分别表示为和因此:

由振动能量公式可知制动盘振动能量EB0为

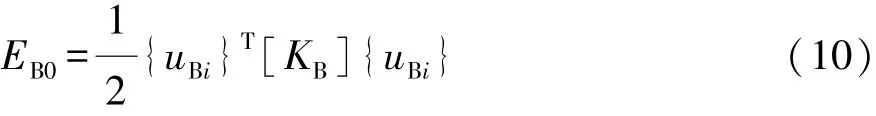
将式(9)代入式(10)，得

制动器第i阶系统模态制动盘振动能量为

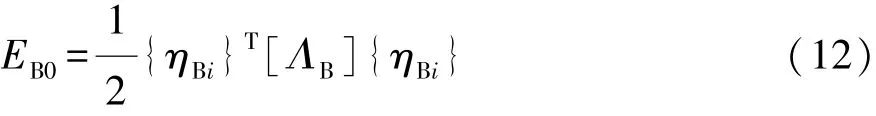
式中:{ηBi}为所分析系统第i阶模态的右特征向量的模；[ΛB]为制动盘的模态角频率平方的对角矩阵。

2.2 “静态”闭环耦合模型制动盘能量计算

用力锤敲击制动器作为其振动的初始状态，视为“静态”。在“静态”条件下，即在制动盘施加转矩，制动缸施加制动压力，使系统各子结构界面耦合，模拟实际制动工况的接触状态，但制动盘在静摩擦作用下处于静止状态。此时，敲击制动系统，制动器只存在高频小振幅的振动，可以认为耦合界面间无相对滑动，只有静摩擦力，其所对应的模型为无动摩擦耦合的静态闭环耦合模型，可用作计算制动盘无摩擦能量馈入的自身的振动能量，而该模型动力学方程中的耦合刚度矩阵[Kf]中不会出现不对称项，以等效刚度耦合的形式存在:

式中[Ke]描述节点对间受到的静摩擦约束的等效刚度。因为摩擦块材料的硬度远小于制动盘材料，[Ke]近似等于摩擦块受横向剪切力工况下的刚度，本研究中[Ke]根据静力等效计算获得。耦合刚度矩阵[Kf]经此变换后，使系统特征矩阵变为对称阵，式(3)的特征值实部全部为零，即此工况下系统的各阶模态全部为稳定模态。本文中所涉及的接触刚度均为节点分布式参数。

对静态闭环耦合模型进行复特征分析，计算系统的特征向量，并提取制动盘B相应的右特征向量的模{ηBi}，然后利用制动盘的模态综合前本身固有模态角频率平方的对角矩阵[ΛB]，根据式(13)算得无动摩擦耦合的静态条件下，制动器系统频率为13kHz的模态的制动盘一个振动周期的总能量EB0＝6.4709×109。注意:本文中算出能量的数值是通过特征向量无量纲化的参数计算的，不表示实际能量，只是为了相对比较，下同。

2.3 动态闭环耦合模型制动盘能量计算

在动态条件下，即在制动盘沿一个方向旋转，制动缸加载制动压力，模拟制动过程，此时制动盘与制动块之间存在动摩擦，以方向恒定的动摩擦力表征，该模型动力学方程中的耦合刚度矩阵[20－21]可表示为

可以看出，[Kf]中出现了不对称项。对动态闭环耦合模型进行复特征分析，计算系统的特征向量，并提取制动盘B相应的右特征向量的模{ηBi}，然后利用制动盘的模态综合前本身固有模态角频率平方的对角矩阵[ΛB]，根据式(14)计算动摩擦耦合的动态条件下，制动器系统模态频率为13kHz模态的制动盘一个振动周期的总能量 EBd＝6.6282×109。

3 摩擦耦合界面能量流动分析

3.1 外制动块A与制动盘B界面能量流动

对于外制动块A和制动盘B耦合的某一对节点，沿z轴正方向看过去，A节点的受力如图 3所示。

设A和B对应节点的位移为(xa，ya，za)和(xb，yb，zb)，作用在 A 和 B 节点上的力分别为(Fax，Fay，Faz)和(Fbx，Fby，Fbz)，各个位移和力的正方向和对应坐标轴正方向相同，摩擦力大小分别为Faf和Fbf，摩擦力方向根据相对运动方向确定。设摩擦因数为μ，界面耦合刚度为K，考虑到各个位移和力的方向，由库伦摩擦定律可推导出节点A和B在x和y方向的受力为

图3 A-B耦合节点的受力

节点A和B在x，y和z方向上的位移为复数，分别将其幅值表示为 Aax，Aay，Aaz，Abx，Aby，Abz；相位为 θax，θay，θaz，θbx，θby，θbz；设在制动系统某 1 阶不稳定模态，振动角频率为ω时，A和B耦合界面的节点的振动方程分别为

在一个振动周期(T＝2π/ω)内，制动块A与制动盘B界面耦合力对A在x，y和z方向上做的功，即从制动块A流入制动盘B的振动能量分别为

对于Ebax，将式(15)、式(16)和式(17)代入式

(18)可得

根据积化和差公式，且因三角函数在一个或多个周期的积分为0，故得

最终得到Ebax表达式为

同理，可得到Ebay表达式为

得到Ebaz最终表达式为

由于振动能量传递是相互的，制动盘B向制动块A传递振动的同时制动块A向制动盘B传递振动。同理可得，在一个振动周期(T＝2π/ω)内，制动块A与制动盘B界面耦合力对B在x，y和z方向上做的功分别为

3.2 内制动块C与制动盘B界面能量流动

同理，对于内制动块C和制动盘B耦合的某一对节点，沿z轴负方向看过去，C的节点的受力如图4所示。

图4 C-B耦合节点的受力

可得相关能量计算表达式如下。

其中制动盘B向制动块C传递振动:

而制动块C向制动盘B传递振动:

3.3 振动能量流动分析

制动器在制动过程中，由于摩擦耦合作用，不断向系统馈入振动能量，在制动块与制动盘的接触耦合界面之间流动，制动块的部分振动能量会流入制动盘中，同时制动盘的部分振动能量也会流入制动块中。以13kHz噪声频率为例，计算相应的振动能量流动。

一个周期内，制动盘B流入制动块A振动能量为

Eba＝Ebax＋Ebay＋Ebaz＝1.05×108

一个周期内，制动块A流入制动盘B振动能量为

Eab＝Eabx＋Eaby＋Eabz＝1.09×106

最终得到:Eab≪Eba

同理，制动盘B流入制动块C振动能量为

Ebc＝Ebcx＋Ebcy＋Ebcz＝5.18×107

制动块C流入制动盘B振动能量为

Ecb＝Ecbx＋Ecby＋Ecbz＝4.07×105

最终得到:Ecb≪Ebc

可见，13kHz高频噪声频率时，制动盘流入制动块的能量比制动块流入制动盘的能量高两个数量级，该制动系统耦合界面的振动传递以制动盘振动向制动块传递为主导，最终得到制动块流入制动盘的总能量为

ET＝Eba－Eab＋Ebc－Ecb＝1.56×108

4 制动盘振动能量平衡分析

根据能量平衡原则，制动盘动态条件下的振动能量为制动盘静态条件下振动能量与流入制动盘能量之和:

由第2节和第3节制动盘相关振动能量的计算，得到制动盘在13kHz频率高频制动尖叫时，动态条件下的振动能量为EBd＝6.6282×109，静态条件下的振动能量为EB0＝6.4709×109，制动盘流出能量为ET＝1.56×108，ET与 EB0之和为 6.6269×109，与 EBd之间的误差为0.024%。各个阶次噪声模态振动能量平衡分析如表2所示，能量平衡误差最大为1.534%，其他阶次均小于1.0%，说明制动盘振动能量满足平衡条件，也证明制动盘振动能量相关推导是可靠和准确的。

表2 各阶次噪声模态振动能量平衡分析

根据3.3节振动能量流动分析结果，可知制动系统的振动能量会不断地从制动盘流入制动块，这一结论与文献[22]中的研究结果一致。而制动器在制动过程中，不断馈入制动系统振动能量，会通过耦合界面带动制动器的机械结构高频振动而产生刺耳的尖叫噪声。今后进一步研究的重点是对本文中进行的制动盘耦合界面的振动能量流动和能量平衡分析，通过更为精简的模型和试验进行验证，尽管后者有一定的难度。

5 结论

(1)利用振动理论和模态分析理论，推导了制动器第i阶系统模态制动盘振动能量表达式，计算了13kHz频率制动盘在静态和动态闭环耦合模型中自身振动能量；

(2)推导闭环耦合模型中制动块和制动盘界面能量流动表达式，并分别计算系统在13kHz噪声频率内外制动块与制动盘间振动能量流动，指出制动器在耦合界面的振动传递以制动盘振动向制动块传递为主导；

(3)通过制动盘振动能量平衡分析，验证了制动盘自身振动能量表达式与摩擦耦合界面能量流动公式的可靠性和有效性，指出在制动过程中，摩擦耦合馈入制动系统的振动能量会通过摩擦耦合界面不断流入，而关键子结构制动盘上的振动随着制动盘旋转辐射，带动周围空气高频振动，是产生高频制动尖叫的主要原因，制动盘是影响其产生的关键子结构。

[1] 杜永昌，高普，王宇健，等.闭环耦合模型中制动盘重根模态[J].清华大学学报:自然科学版，2016(2):117－123.

[2] 管迪华，杜永昌，王霄锋，等.对一盘式制动器高频尖叫及抑制的分析[J].工程力学，2014，31(12):217－222.

[3] SINCLAIR D，MANVILLE N J.Frictional vibration[J].Journal of Applied Mechanics，1955，22:207－214.

[4] CHIKAROMISS.Study of brake noise[J].Mitsubishi Technology Review，1968，5(1).

[5] SPURR R T.A theory of brake squeal[J].Proceedings of the Institution of Mechanical Engineers:Automobile Division，1961，15(1):33－52.

[6] LILES G D.Analysis of disc brake squeal using finite element methods[C].SAE Paper 891150.

[7] 陈小悦.鼓式制动器低频振颤的研究[D].北京:清华大学，1988.

[8] ZHU Xinchao，GUAN Dihua.The experimental and simulational analysis on drum brake squeal by structurally closed-loop coupling model[C].SAE Paper 931879.

[9] 蒋东鹰，管迪华.用闭环耦合模型对盘式制动器制动尖叫的研究[J].清华大学学报:自然科学版，1998，38(1):68－71.

[10] KUMEMRURA Y，GAMO Y，KONO K，et al.Analysis for reducing low frequency squeal of Disc Brake[C].SAE Paper 2001－01－3137.

[11] 蒋东鹰.盘式制动器制动尖叫的研究[D].北京:清华大学汽车工程系，1998.

[12] 宿新东.抑制制动器振动噪声的子结构灵敏度分析和结构修改设计方法研究[D].北京:清华大学汽车工程系，2003.

[13] GUAN Dihua，JIANG Dongying.A Study on disc brake squeal using finite element methods[C].SAE Paper 980597.

[14] GUAN Dihua， SU Xindong， ZHANG Fang.Sensitivity analysis of brake squeal tendency to substructures’modal parameters[J].Journal of sound and vibration，291(1):72－80，2006.

[15] 管迪华，宿新东.制动振动噪声研究的回顾，发展与评述[J].工程力学，2004，21(4):150－155.

[16] 戢何民.某型轿车盘式制动器制动噪声的控制[J].汽车技术，2011(11):20－22.

[17] CHEN F， QUAGLIA R L， TAN C A.On automotive disc brake squeal Part I:Mechanisms and causes[C].SAE Paper 2003－01－0683.

[18] GUAN Dihua，HUANG Jinchun.The method of feed-in energy on disc brake squeal[J].Journal of Sound and Vibration，2003，261(2):297－307.

[19] 傅志方.模态分析理论与应用[M].上海:上海交通大学出版社，2000.

[20] 高普.盘式制动器噪声闭环耦合模型建模方法研究[D].秦皇岛:燕山大学，2015.

[21] 高普，杜永昌，王宇健.盘式制动器闭环耦合模型耦合刚度的优化[J].汽车工程，2016，38(11):1357－1361.

[22] VON WAGNER U，HORNING S，GRÄBNER N，et al.Methods for rapid development of silent brakes-actual research and future prospects[C].Proceedings of 32nd International mu Symposium，VDI Fortschritt Berichte 773，2013:268－299.