稳健最小二乘单类支持向量机及其稀疏化方法
王瑞平,方云录,何洪辉
(1.安阳工学院 计算机科学与信息工程学院,河南 安阳 455000;2.河南大学 民生学院,河南 开封 475001;3.河南大学 软件学院,河南 开封475001)
0 引 言
单分类支持向量机(one class support vector machine,OCSVM)需要求解一个带不等式约束的二次规划问题,计算复杂度较高。针对此问题,有学者提出了最小二乘单类支持向量机[1,2](least square one class support vector machine,LS-OCSVM),其基本思想与最小二乘支持向量机(least square support vector machine,LS-SVM)类似[3,4],通过引入等式约束和最小二乘损失函数,将其转化为一线性方程组的求解问题,大大提高了计算效率。
与LS-SVM类似,LS-OCSVM存在易受噪声样本影响、稀疏性差的问题。针对此问题,常采用普通LS-SVM方法对目标样本进行分类,然后根据第一步求得的样本误差值确定对应样本的权值,最后采用加权的LS-SVM方法对样本进行再次分类。模型稀疏化采用迭代训练策略,当模型的测试误差不超过给定阈值时,对每个样本的拉格朗日乘子的绝对值|αi|进行升序排序,在每次迭代计算中,去掉前5%个乘子所对应的样本,然后继续在新的样本集上进行训练并估计测试误差,直至满足稀疏化要求。余正涛等[5]提出一种基于主动学习的LSSVM稀疏化方法,首先采用核聚类选取初始样本,建立一个LSSVM最小分类器,然后求解样本在分类器作用下的分布,选择最接近分类面的样本并将其加入训练集建立新的分类器,重复上述过程直到模型精度满足要求,以此建立部分样本的LSSVM稀疏化模型。文献[6]采用独立成分分析(ICA)对语音特征降维,对降维后的语音样本采用LSSVM构建建模,实现基于ICA的快速剪枝方法,完成支持向量筛选。文献[7-9]采用在线稀疏化策略,实现LSSVM的快速稀疏化。此外,Carvalho等[10]提出一种针对LS-SVM的两步稀疏化方法,该方法是根据样本到超平面的距离确定是否对样本进行保留。本文提出一种稳健加权的最小二乘单类支持向量机(robust LS-OCSVM,RLS-OCSVM),采用普通最小二乘单类支持向量机获取样本训练误差,并选用不同的权函数对样本进行加权分类,最后通过迭代计算实现样本分类。同时,提出一种模型的稀疏化方法(RLS-OCSVM-GA),以训练精度最大化和支持向量最小化为目标,采用多目标遗传算法实现模型的稀疏化。
1 稳健最小二乘单类支持向量机
最小二乘单类支持向量机采用二次损失函数和等式约束,以训练样本到超平面的距离最小化求解超平面,因此,大多数训练样本将位于超平面附近,从而可以根据样本到超平面的距离表示样本与训练样本的接近程度。
1.1 最小二乘单类支持向量机
最小二乘单类支持向量机是单类支持向量机的一种扩展,其目标函数为
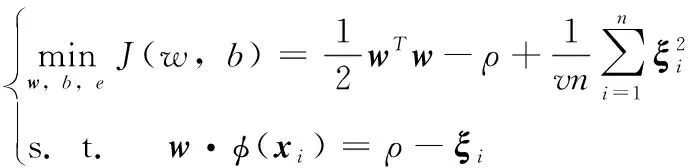
(1)
与OCSVM相比,不再具有ξi≥0约束,且松弛因子变为平方项。引入拉格朗日乘子αi,分别对w、ξ、ρ、αi求导并令其为0,则
(2)
上式可化简为
(3)
其中,1=[1,1,…,1]T,α=[α1,α2,…,αn]T,Ω为核函数矩阵,Ωi,j=K(xi,xj)=φ(xi)Tφ(xj)。上式为线性方程组,计算速度较二次优化问题大大提高。
求得的超平面为
(4)
1.2 稳健最小二乘单类支持向量机
为得到稳健的分类模型,基于LS-OCSVM的解,可以得到一个误差变量ξi=αivn/2,则目标函数可表示为
(5)
同样对w、ξ、ρ、αi求导并令其为0,并化简,则
(6)
为叙述方便,将上式改写为
(7)
权值μi可由(非加权)LS-OCSVM误差项ξi得到,权函数可以采用Hampel等稳健权函数
(8)
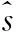
2 基于GA的最小二乘单类支持向量机稀疏化
标准的单类支持向量机所求得的拉格朗日系数αi中有较多0值,具有稀疏性,但是在LS-OCSVM中,由于最优条件中含有αi=2μiξi/vn,因此不具有稀疏性。在非稀疏条件下,几乎所有的训练样本都被用于最终的决策函数,当训练样本较大时,将严重影响预测速度,所以稀疏化是LS-OCSVM的一项重要研究内容。
稀疏化最理想的情况是在保持精度不降低的前提下尽量减小支持向量数,可以将其视为一个多目标规划问题,本文尝试采用遗传算法进行稀疏化。
对每个样本值采用二进制编码,“1”代表支持向量,“0”代表非支持向量。由式(7)可知,与稀疏化直接相关的是矩阵A,一般的剪枝方法是将非支持样本在矩阵A中所对应的行和列删除,保留支持向量对应的行和列,然后再求解拉格朗日系数,这种方法虽易于实现,但会导致样本信息的丢失。本文根据染色体编码,只将编码“0”在矩阵A中所对应的列删除,保留其所在的行,从而最大限度地保留样本信息。
稀疏化过程中,应尽量满足分类精度最大化和支持向量数最小化,遗传算法的适应度函数为
(9)
其中,σi为训练精度,ri为稀疏化比例,即非支持向量数与总样本数之比,λ∈[0,1]为调节系数,用于调节训练精度与稀疏化在适应度函数中所占的比例。
为使迭代过程快速收敛,采用启发式设计,基于遗传算法的稳健最小二乘单类支持向量机稀疏化方法具体步骤如下:
(1)采用普通最小二乘单类支持向量机对样本进行训练,得到初始样本误差;
(2)根据初始样本误差,计算样本权值,由式(8)计算系数矩阵和样本误差;
(3)重复步骤(2)直至两次迭代误差小于阈值,得到系数矩阵A和初始分类精度σ;
(4)设置进化代数T,初始化代数t=0;
(5)产生初始种群P(t),对每个样本进行染色体编码;
(6)根据染色体编码,当编码为“0”时,删除系数矩阵A中的对应列,并由式(7)求解最小二乘支持向量机模型;
(7)计算每个个体的分类精度σi,t、稀疏化程度ri,t以及适应度函数值fi,t;
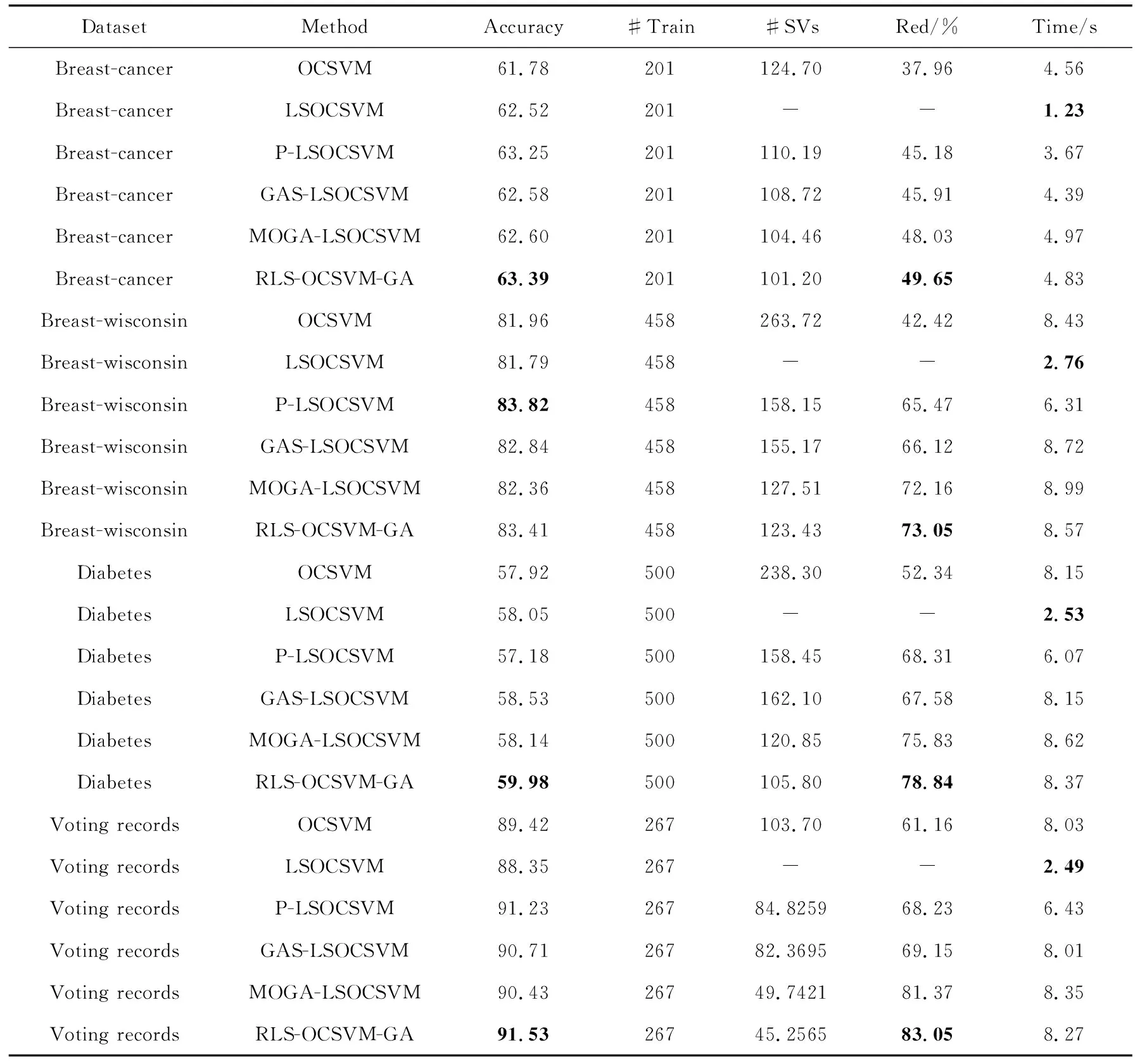
(8)当t 1)根据适应度值选择下一代个体; 2)按交叉概率进行交叉操作; 3)按变异概率进行变异操作; 4)令t=t+1,生成下一代种群P(t+1)并按步骤(6)、步骤(7)计算分类精度ai,t+1、稀疏化程度ri,t+1和适应度函数值fi,t+1; (9)选择适应度值最大的个体,其对应的模型解即为需要求解的稀疏化模型参数。 需要特别指出的是,在染色体编码时,第一个编码应始终为“1”,因为系数矩阵A中的第一行和第一列均为常数,不是样本所对应的行和列,因此不应该被删除。 为验证本文算法的有效性,采用一组UCI数据集作为分类对象,将数量较多的一类作为目标类,另一类作为异常类,采用的数据见表1,括号中的数字为数量较少类的样本数。为保证目标数据的代表性,随机选取80%目标类样本作为训练样本,剩余的20%目标样本和全部异常样本作为测试样本。 表1 实验数据集 将提出的算法与典型稀疏化方法进行对比分析,用于对比分析的典型稀疏化方法有文献[10]的剪枝方法、Silva等[11]提出的GAS-LSSVM和MOGAS-LSSVM方法,但这3种稀疏化方法都是针对LSSVM模型提出的,而本文研究对象为单类支持向量机,为便于比较,将3种方法目标函数改为对应的单类支持向量机形式,其余稀疏化步骤不变,所得到的模型分别简称为P-LSOCSVM、GAS-LSOCSVM、MOGA-LSOCSVM。这些改进易于理解且较为简单,故本文不再赘述。 RLS-OCSVM-GA稀疏化模型中取λ为1,因为当λ在区间[0,1]之间变化时精度变化不大,但是稀疏化程度将随着λ的增大而提高,而我们的目标是在保证精度的前提下尽量得到稀疏化模型。遗传算法均采用二进制编码,进化代数为50,种群大小为20,每个变量的二进制长度为系数矩阵列数。每个实验进行10次并取其精度和稀疏化的均值,各模型的超参数采用5-fold交叉验证进行确定,实验结果见表2,其中最优结果用粗体标识 (10) 由表2可知,在分类精度方面,P-LSOCSVM与RLS-OCSVM-GA的分类精度基本相当,均优于OCSVM、LS-OCSVM、GAS-LSOCSVM和MOGA-LSOCSVM,表明提出方法的分类性能具有较强的稳健性。由于采用相似的权函数确定方法,因此P-LSOCSVM与RLS-OCSVM-GA的分类精度较为接近,但总体而言提出的方法在稳健性方面优于P-LSOCSVM,这是因为提出的方法在稀疏化过程中考虑了分类精度,在采用遗传算法进行稀疏化的过程中通过不断迭代保持甚至略微提高了分类精度。 在稀疏性方面,提出的RLS-OCSVM-GA方法略优于MOGA-LSOCSVM,明显优于OCSVM、P-LSOCSVM、GAS-LSOCSVM,这是因为前两种方法以分类精度最高和稀疏性最大为目标,从而保证了种群在迭代的过程中模型向的稀疏化高的方向发展,而其余方法由于在目标函数未考虑模型的稀疏性,导致其稀疏性不及前两种方法,但是P-LSOCSVM、GAS-LSOCSVM在通过不断迭代提高模型的分类精度的同时也剔除了系数矩阵的部分列向量,从而也在一定程度上保证了模型的稀疏性。 表2 分类精度与稀疏化程度 在方法的复杂度方面,LSOCSVM由于不需要迭代进行稀疏化,因此其复杂度最低,提出的方法采用迭代方式对稀疏化模型进行求解,其复杂度略高于OCSVM,但与其余的稀疏化方法相当。 由以上分析可知,提出的RLS-OCSVM-GA方法在保持分类精度的同时,具有较好的稀疏性。 本文以提高最小二乘单类支持向量机的稳健性与稀疏性为目标,提出了基于迭代加权的最小二乘单类支持向量机,并给出了基于遗传算法的稀疏化方法,与传统方法相比,提出的方法具有以下优势:①通过权函数的不断迭代保证了模型的稳健性;②基于遗传算法的稀疏化方法以分类精度最高和稀疏性最大为目标,在稀疏化的过程中只删除系数矩阵所对应的列,最大限度地保持了样本信息。实验结果表明,本文提出的RLS-OCSVM-GA模型在稳健性及稀疏性方面均优于传统方法。 参考文献: [1]Wang T,Chen J,Zhou Y,et al.Online least squares one-class support vector machines-based abnormal visual event detection[J].Sensors,2013,13(12):17130-17155. [2]Uddin M S,Kuh A.Online least-squares one-class support vector machine for outlier detection in power grid data[C]//IEEE International Conference on Acoustics,Speech and Signal Processing.IEEE,2016:2628-2632. [3]Huang X,Shi L,Suykens J A K.Asymmetric least squares support vector machine classifiers[J].Computational Statistics & Data Analysis,2014,70:395-405. [4]Rebentrost P,Mohseni M,Lloyd S.Quantum support vector machine for big data classification[J].Physical Review Letters,2014,113(13):130503. [5]YU Zhengtao,ZOU Junjie,ZHAO Xing,et al.Sparseness of least squares support vector machines based on active learning[J].Journal of Nanjing University of Science and Technology,2012,36(1):12-17(in Chinese).[余正涛,邹俊杰,赵兴,等.基于主动学习的最小二乘支持向量机稀疏化[J].南京理工大学学报(自然科学版),2012,36(1):12-17.] [6]WANG Zhenzhen,ZHANG Xueying,LIU Xiaofeng.Sparse LSSVM and application in speech recognition[J].Computer Engineering and Design,2014,35(4):1303-1307(in Chinese).[王真真,张雪英,刘晓峰.稀疏LSSVM及其在语音识别中的应用[J].计算机工程与设计,2014,35(4):1303-1307.] [7]Cheng R,Song Y,Chen D,et al.Intelligent localization of a high-speed train using LSSVM and the online sparse optimization approach[J].IEEE Transactions on Intelligent Transportation Systems,2017,99:1-14. [8]Gao Y,Shan X,Hu Z,et al.Extended compressed tracking via random projection based on MSERs and online LS-SVM learning[J].Pattern Recognition,2016,59(C):245-254. [9]Wang B,Shi Q,Mei Q.Improvement of LS-SVM for time series prediction[C]//11th International Conference on Service Systems and Service Management.IEEE,2014:1-5. [10]Carvalho B P R,Braga A P.IP-LSSVM:A two-step sparse classifier[J].Pattern Recognition Letters,2009,30(16):1507-1515. [11]Silva D A,Silva J P,Neto A R R.Novel approaches using evolutionary computation for sparse least square support vector machines[J].Neurocomputing,2015,168:908-916.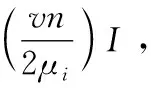
3 实验与分析
4 结束语

