改进的随机聚点搜索算法在河网水力学模型糙率反演优化中的应用

杜艳艳，王 伟

(辽宁天阳工程技术咨询服务有限公司，辽宁 沈阳 110001)

对于平原河网而言，需要采用水力学模型对其不同断面的流速和水位进行推算。而水力学模型的重要参数为河网的糙率，糙率参数的选择对于平原河网水位和流速的推算精度高低十分重要。当前，对于平原河网糙率的反演优化成为国内学者的研究热点，并取得一定的研究成果[1- 5]，这些成果大都采用试错方法对河道糙率进行反演分析，但是对于平原河网水力学模型糙率反演优化的研究还较少，近些年来，随机聚点算法由于综合多种优化算法的特点，在变量优化求解领域中应用效果较好[6- 9]，但是传统随机聚点算法存在计算速率较慢，受优收敛精度的局限，为此有学者针对这些局限，对传统随机聚点算法进行改进，并将该优化算法引入到平原河网河网水力学模型糙率反演优化中，从而寻求一种有效的平原河网糙率反演优化的方法。

1 改进的随机聚点搜索算法原理

改进的随机聚点搜索算法以变量随机概率为搜索聚点，其搜素几率计算方程为：

Pi∞exp(-Xi)

(1)

式中，Pi—聚点i附近的搜索概率；Xi—搜素指标的等级。

改进的随机聚点搜索算法对传统算法的搜素概率进行比例调整，从而对传统算法进行改进，其改进后的搜素几率计算方程为：

(2)

式中，kB—新的搜素几率因子；Xt—调整后的搜素指标的等级。

改进的随机聚点搜索算法对不同变量进行势能的计算，计算方程为：

(3)

式中，a、b—势能拟合项的系数；rij—不同变量因子之间的势能间距；q—变量因子。

不同变量因子之间的势能间距计算方程为;

(4)

式中，r1i，r2j—不同变量单因子势能间距；A—旋转的转置矩阵；r—矩阵权重因子。

在具体应用时，需要选用评价指标来分析目标优选好坏，本文选用效率系数值来评价平原河网糙率反演优化的精度，效率系数计算方程为：

(5)

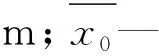
平原河网糙率反演需要对确定目标的寻优值，本文以水位作为平原河网糙率反演优化的目标值，其优化方程为：

(6)

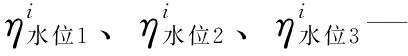
本文采用圣维南方程组对河道水力学进行求解，该方程组的主要计算原理见参考文献[10]。

2 实例应用

2.1 平原河网概况

本文以辽宁中部某平原河网为研究实例，该平原河网内有主要8个河段，各个河段的主要特征参数见表1。为定量分析不同算法下的糙率反演优化精度，在8个河段均设置有水位和流速测验断面，结合各河段实测水力学数据对比分析不同算法下各河段糙率反演优化的收敛和计算精度。

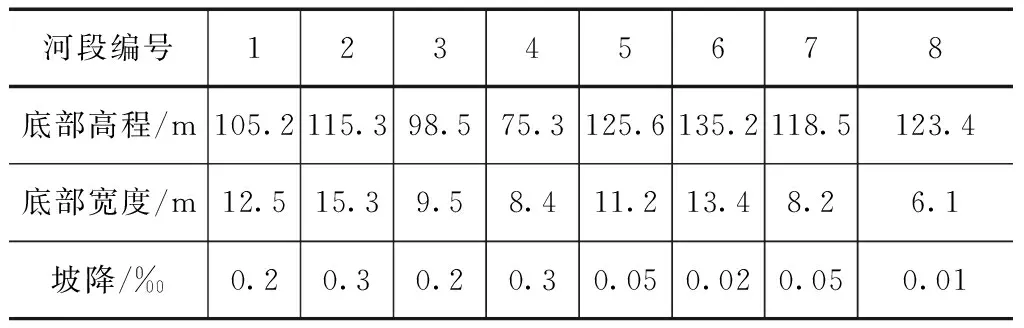
表1 平原河网各河段主要特征参数

2.2 不同算法下后验糙率误差分析

为对比分析不同算法下后验糙率的误差影响，结合不同算法对各河段后验糙率反演误差进行了分析，分析结果见表2、3。

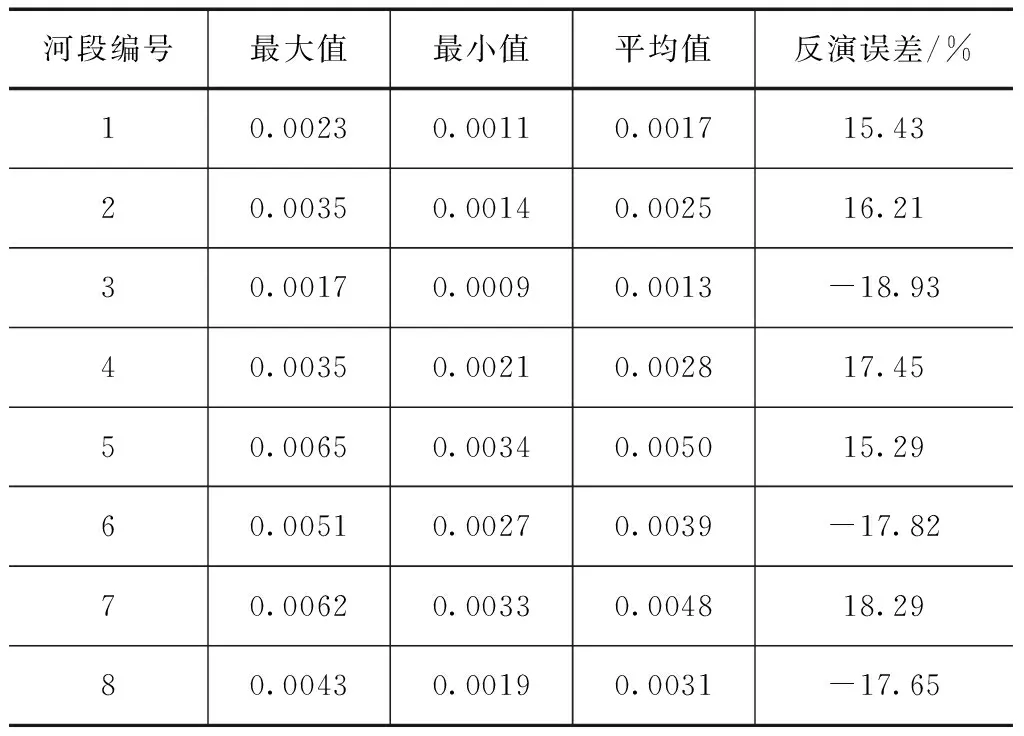
表2 传统算法下的各河段后验糙率误差分析结果

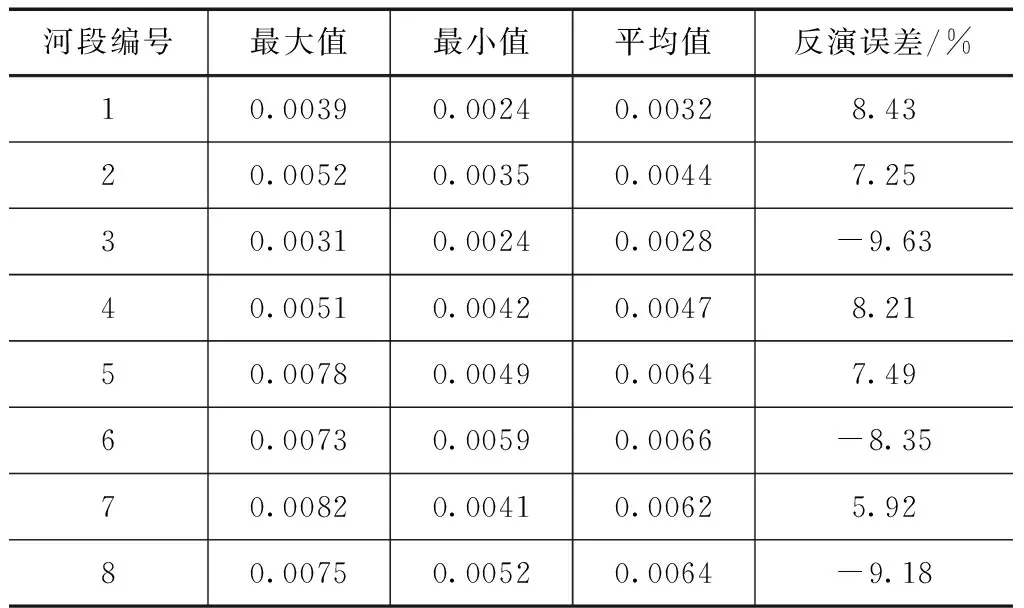
表3 改进算法下的各河段后验糙率误差分析结果

从表2、3中可以看出，改进算法下各河段的后验糙率的最大值、最小值以及均值都要大于传统算法的下的后验糙率值，这主要是因为改进的随机聚点搜索算法对搜索因子进行等级调整，使得该算法下糙率寻优迅速集中，提高了糙率反演寻优的计算精度，相比于传统算法，改进算法下各河段后验糙率反演误差减少9.1%，糙率反演优化效果明显好于传统算法。

2.3 不同算法下糙率反演收敛精度分析

考虑到不同算法下糙率反演的收敛精度不同，选取4个典型河段分析不同算法下糙率反演优化的迭代次数，分析结果如图1所示。

从图1中可以看出，选取的典型4个河段，改进算法下糙率反演优化迭代次数明显少于传统算法，相比于传统算法，其寻优迭代次数平均减少19次，表明了改进算法下糙率反演优化求解的收敛度要好于传统算法，改进算法下平原河网糙率反演寻优速率要快于传统算法，解决传统算法寻优时间长、速率慢的局限。

2.4 不同算法的糙率反演优化精度对比分析

基于圣维南方程组并结合各河段实测水位和流速对比分析不同算法下反演优化糙率的计算精度，分析结果见表4、5及图2。

从表4、5中可以看出，相比于传统算法，改进算法后糙率优化反演后推算的各河段水位及流速和实测值之间的误差明显低于传统算法，水位和流速反演误差分别减少13.3%和14.2%，糙率反演优化计算精度改善效果明显，这主要是因为改进算法其计算寻优收敛率得到显著提高，也使得其寻优解更为合理，因此改进算法下河网内各河段的水位和流速反演精度相比于传统算法也得到明显改善。从图2中可以看出，改进算法下的水位和流速与实测值的相关度都明显高于传统算法。综上，改进的随机聚点搜索算法在平原河网糙率反演优化计算中适用性明显好于传统算法。

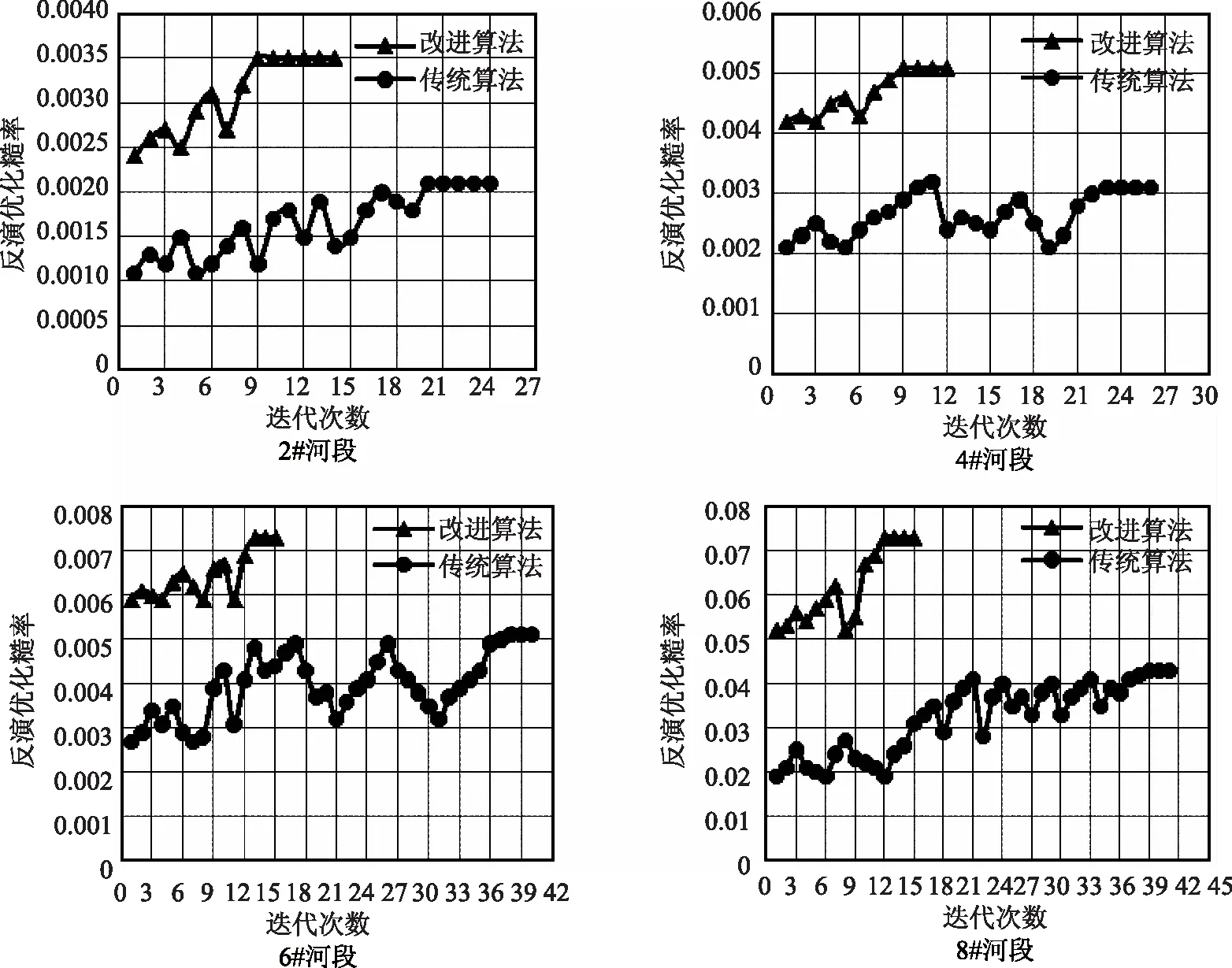
图1 各算法下不同河段收敛精度对比分析结果

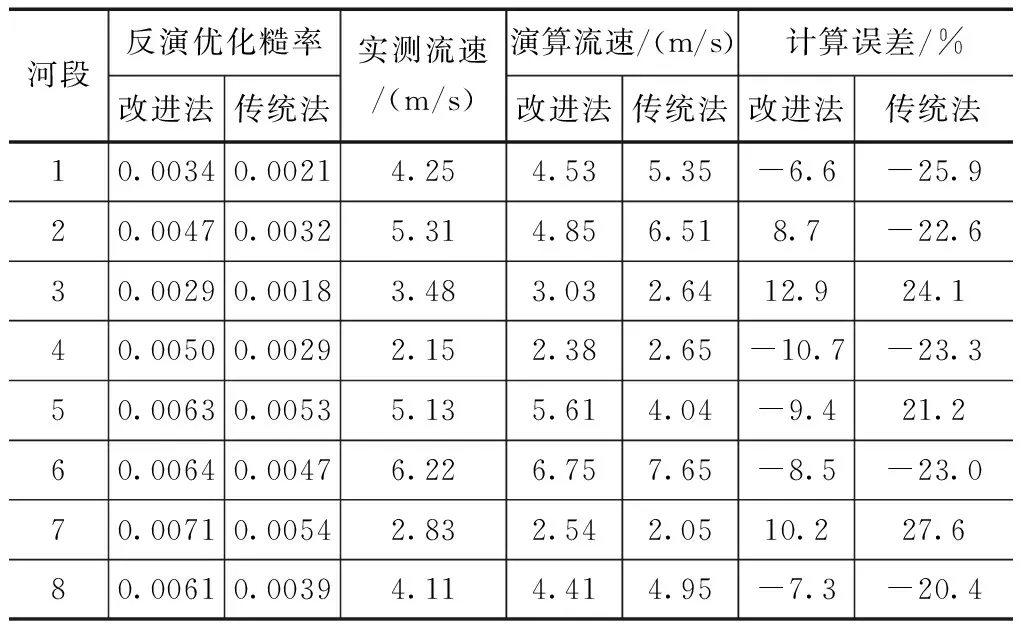
河段反演优化糙率改进法传统法实测流速/(m/s)演算流速/(m/s)计算误差/%改进法传统法改进法传统法10.00340.00214.254.535.35-6.6-25.920.00470.00325.314.856.518.7-22.630.00290.00183.483.032.6412.924.140.00500.00292.152.382.65-10.7-23.350.00630.00535.135.614.04-9.421.260.00640.00476.226.757.65-8.5-23.070.00710.00542.832.542.0510.227.680.00610.00394.114.414.95-7.3-20.4

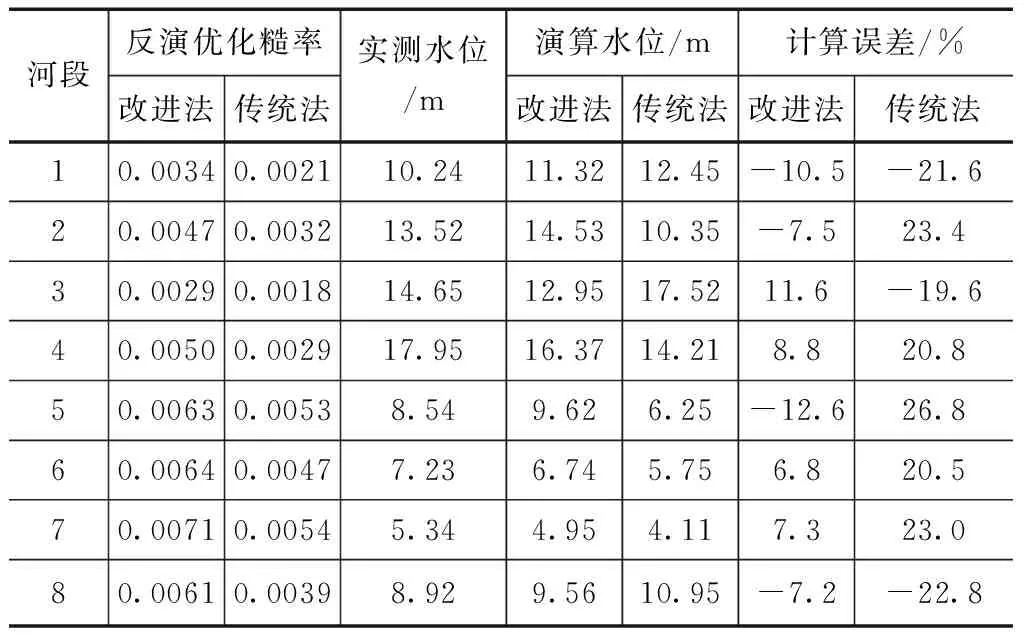
表5 不同算法下各河段糙率反演优化的水位值与实测值误差分析结果

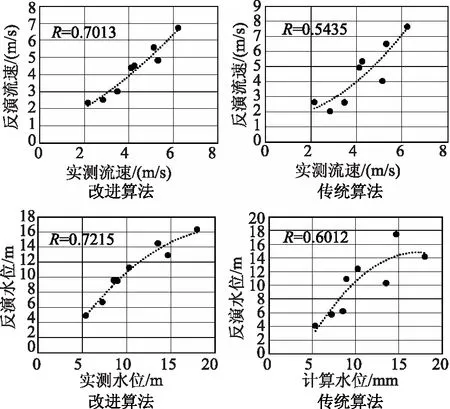
图2 不同算法下的反演水力学特征和实测值之间的相关性分析结果

3 结语

本文结合改进的聚点搜索算法并结合圣维南方程对辽宁中部某平原河网水力学模型糙率进行反演优化研究，对比分析取得以下结论：

(1)相比于传统算法，改进算法下糙率寻优下降更为集中，反演误差得到较大程度改善，该算法下糙率反演优化更为合理有效。

(2)经与实测水位流速数据对比，相比于传统算法，改进算法在平原河网水力学模型糙率反有优化精度得到较大程度改善，反演误差降低明显，改进算法解决了传统算法计算时间长，效率低的局限。

[1] 包红军, 赵琳娜. 基于Kalman滤波糙率反演模型的河道洪水实时预报研究[J]. 水力发电学报, 2012(03): 59- 64.

[2] 贾铭洋. SonTek-IQ与雷达水位计在输水工程试算糙率中的应用[J]. 水利规划与设计, 2015(10): 48- 51.

[3] 李丽, 王加虎, 王建群, 等. 自适应随机搜索算法在河网数学模型糙率反演中的应用[J]. 水利水电科技进展, 2011(05): 64- 67.

[4] 沈军云, 陈学林, 刘涛. 黑河莺落峡河段糙率分析及其计算[J]. 水利规划与设计, 2011(04): 42- 45.

[5] 程伟平, 刘国华. 基于广义逆理论的河网糙率反演研究[J]. 浙江大学学报(工学版), 2005(10): 145- 150.

[6] 任强. 跨流域调水工程输水建筑物糙率研究[J]. 水利规划与设计, 2010(03): 43- 45+65.

[7] 郭建青, 周宏飞, 李彦, 等. 随机搜索算法在确定含水层参数中的应用[J]. 中国农村水利水电, 2010(12): 48- 51+56.

[8] 郭建青, 周宏飞, 李彦, 等. 随机搜索算法在确定河流水质参数中的应用[J]. 水文, 2010(02): 25- 28.

[9] 周萃英. 岩体边坡滑裂面随机搜索机理与工程应用——以黄河小浪底水库进口高边坡泻洪、 发电、 引水建筑物进口高边坡为例[J]. 工程地质学报, 2000(02): 169- 174.

[10] 胡庆云, 王船海. 圣维南方程组4点线性隐格式的稳定性分析[J]. 河海大学学报(自然科学版), 2011(04): 397- 401.