局部对称拟常曲率黎曼流形中的紧致子流形

李明图

（天水师范学院 数学与统计学院，甘肃 天水 741001）

文献[1]中研究了Sn+p(1)中具有单位平行平均曲率向量的紧致子流形Mn，得到了Mn的第二基本形式模长平方σ的一个上界.当σ小于或等于此上界时，Mn位于Sn+p(1)的一个n+1维全测地子流形Sn+1(1)中.之后，许洪伟教授[2]和许森林教授[3]利用一定的计算技巧去估计τ的Laplacian,先后对[1]中的结果作了改进.纪永强教授在文献[5]中将[3]中的结论由外围空间是常曲率黎曼空间推广到了局部对称拟常曲率空间的情形.得到如下结果.

定理A设Mn是 n+p维局部对称拟常曲率黎曼流形 Nn+p中的具有单位平行平均曲率向量的n维紧致子流形(p≥2)，若Mn的第二基本形式模长的平方σ满足

则Mn位于Nn+p的一个n+1维全测地子流形Nn+1中.

本文继续研究了局部对称拟常曲率流形具有单位平行平均曲率向量的紧致子流形，在n≥2时，将定理A中的结果做了改进.得到

定理1设Mn是 n+p维局部对称拟常曲率黎曼流形 Nn+p中的具有单位平行平均曲率向量的n维紧致子流形(n,p≥2)，若Mn的第二基本形式模长的平方σ满足

其中则Mn位于Nn+p的一个n+1维全测地子流形Nn+1中.

注：和都是关于正整数n的正函数，(n≥2).定理1中的已有结果大于或等于定理A中的结果.因此优于定理A中的已有结果.

1 预备知识

在本文中，各类指标的取值范围约定如下：

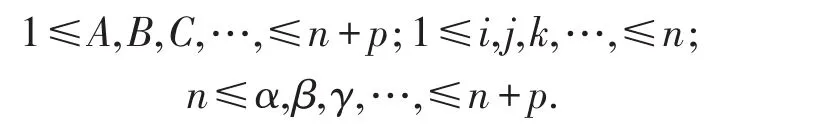
设Nn+p是n+p维局部对称的拟常曲率黎曼流形，Mn是Nn+p中的n维紧致子流形，在 Nn+p上选取局部标准正交标架场 {eA}，使得限制在Mn上，与Mn相切，是在 Nn+p上与{eA}对偶的标架场，{ωAB}是联络形式，限制在Mn上，有

其中h，η，Rijkl，Rαβkl分别表示Mn的第二基本形式，平均曲率向量场，曲率张量场，法曲率张量场，K表示Nn+p的曲率张量场·记则有

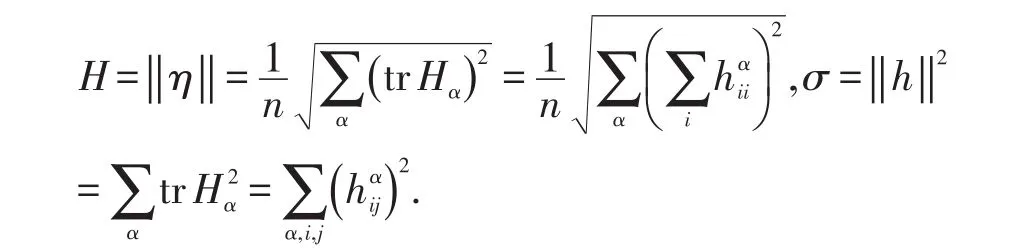
用和分别表示的一阶及二阶共变导数，有

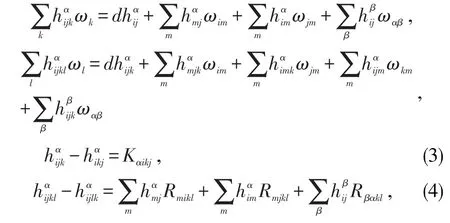
定义由(3),(4)式得到

因为Mn是具有平行平均曲率向量的子流形，于是H=const.

设单位平均曲率向量 η=en+1,则有

由于Nn+p是拟常曲率黎曼流形[4]，于是有

其中a,b是Nn+p上的光滑函数，{ξA}满足

又Nn+p是局部对称的，即有Kαijk;l=0.因此

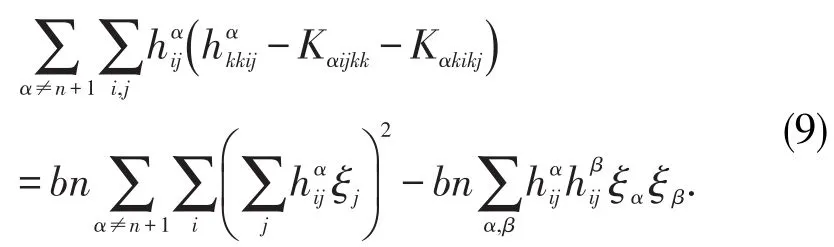
令

选取适当法标架场{eα}，使得矩阵(t r (HαHβ)) 可以对角化，即有

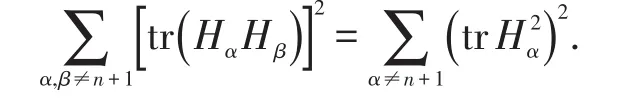
进而，利用(5)，(7)，(8)，(9)式，通过计算得

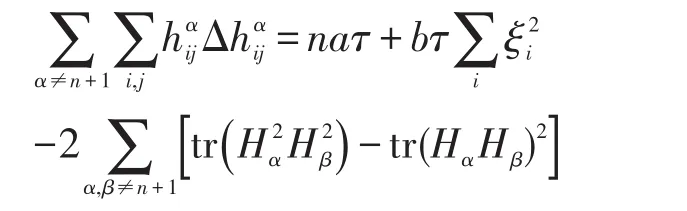
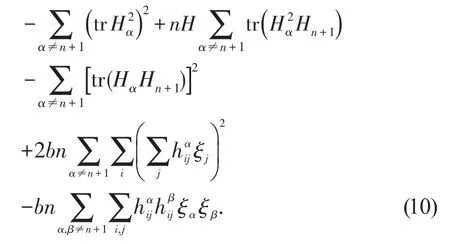
由文献[7]知，下列不等式成立

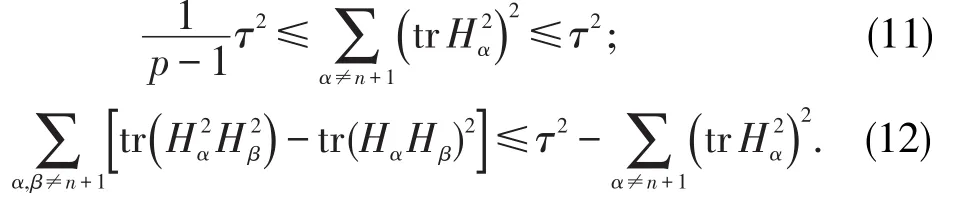
利用Schwarz不等式得到[5]

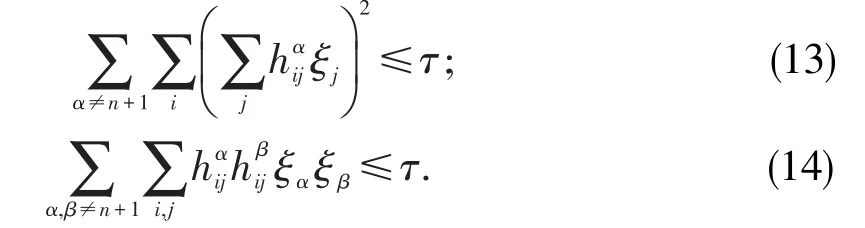
引理1[6]设 x1,x2,…xn,y1,y2,…,yn是 2n个实数，并且满足则有

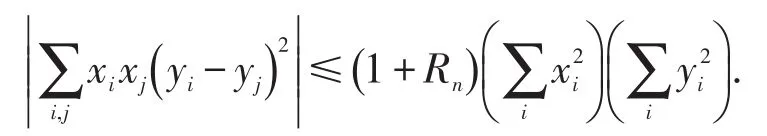
其中

对固定的α≠n+1可将 n阶对称方阵Hn+1,Hα同时对角化.因此有

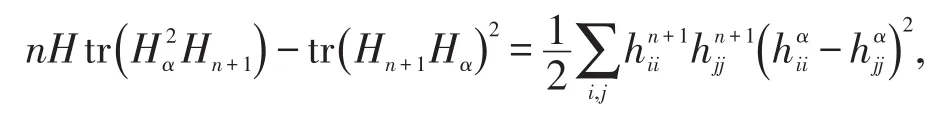
注意到 trHα=∑ihiαi=0,∀α≠n+1，对上式两边关于 α(α ≠n+1) 求和，由引理1可见

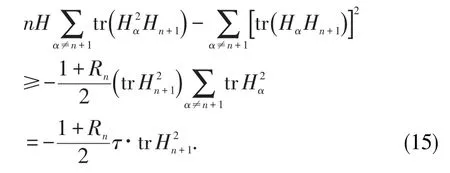
2 定理1的证明

证明由(10),(11),(12)，(15)式得到

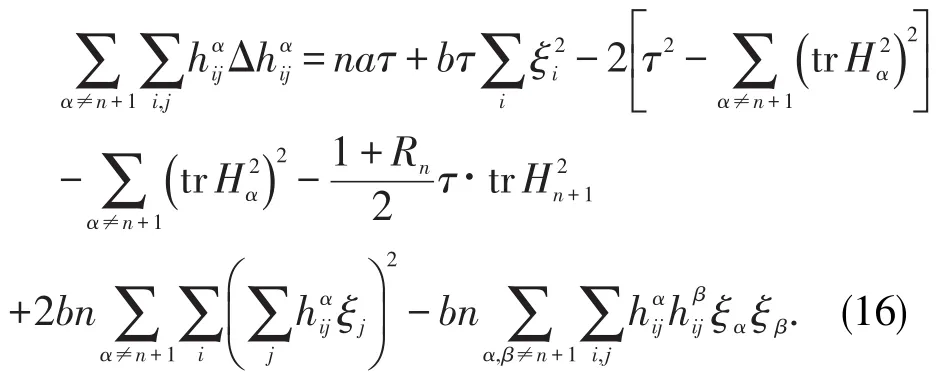
由τ及σ的定义知， 0≤τ≤σ，现分情况讨论如下：

（1） 当 b≥0 时，利用(13)，(14)，(16)式得到

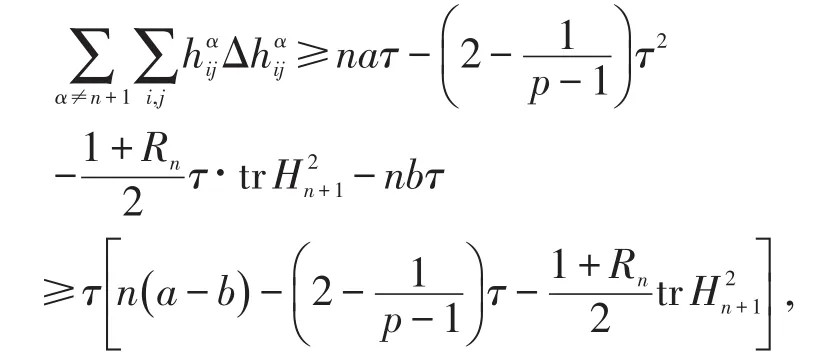
令则有

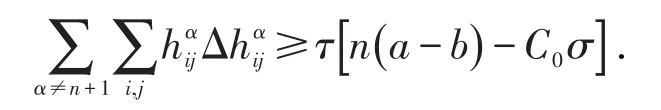
结合τ的定义知

又 Mn紧致，利用Hopf原理可知，当σ≤n(a -b)时，经类似于[5，7]中的讨论，有τ=0.进而由文献[8]知，Mn位于 Nn+p的一个n+1维全测地子流形Nn+1中.

（2）当b＜0时，注意到

利用(13)，(14)，(16)式得到

其中C0同上.从而有又 Mn紧致，利用Hopf原理可知，当

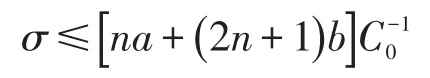
时，便有τ=0.经与(I)中类似的讨论得知，Mn位于 Nn+p的一个n+1维全测地子流形Nn+1中.

统一(1)，(2)两种情形中σ所要满足的关系式,便有

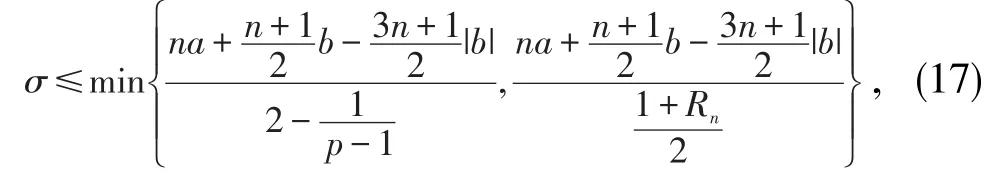
综合上述两种情形可见，当σ满足(17)式时，Mn位于Nn+p的一个 n+1维全测地子流形Nn+1中.证毕.

[1]YAU S.T..Submanifolds with constant mean curva ture[J].I:Amer J Math,1974,96(2):346-366;II:Amer J Math,1975,97(1):76-100.

[2]许洪伟.Simons型Pinching常数和等距浸入问题[J].数学年刊A,1991,12(3):261-269.

[3]徐森林,薛春华.微分几何[M].合肥:中国科学技术大学出版社,1997:224-226.

[4]BAI Z.G..Minimal submanifolds in a Riemannian manifold of quasi-constant curvature[J].Chin Ana of Math,1988,9 B(1):32-37.

[5]纪永强,贺晴.局部对称拟常曲率黎曼流形中具有平行平均曲率向量的子流形[J].西北师范大学学报,2009,45(5):16-18.

[6]张剑锋.局部对称共形平坦黎曼流形中的紧致子流形[J].数学杂志,2004.24(1):7-12.

[7]纪永强.子流形几何[M].北京:科学出版社,2004.

[8]ERBACHER J.Reduction of the codimension of an isometric immersion[J].Diff Geom,1971,(5):333-340.

[9]JI Y.Q.,XU S.L..Minimal submanifolds in locally symmetric spaces[J].Northest Math J,2005,21(1):61-69.

[10]宋卫东.关于局部对称空间中的极小子流形[J].数学年刊(A),1998,19(6):693-698.