Polya坛子抽样模型及其随机模拟
王丙参,魏艳华,张艺馨
(天水师范学院 数学与统计学院,甘肃 天水 741001)
Polya坛子模型是非常重要的概率模型:坛子中有b个黑球与r个红球,每次任取一球,将原球放回后再加入c个同色球和d个异色球,它具有重要的应用价值.[1-4]例如,由其衍生出的Polya分布是一种传染分布或称为概率传染分布,在气候统计中,Polya分布常用来拟合雾、雷暴等.记ξn为n次中抽到黑球的次数,董立华在d=0条件下探讨了的极限分布,[1]努尔买买提斯吉在c=0,d>0条件下得出的极限是取值为0.5的退化分布.[3]很多学者对Polya坛子模型的理论分析都是限于特定条件下进行的,这是因为对一般Polya坛子模型进行理论研究非常困难,甚至无法得出解析结论.近几十年来,鞅论在诸如金融、保险和可靠性理论等实际问题中得到了广泛应用,是理论探讨的一种新方法.[5-6]另外,随机模拟方法是研究复杂系统的一种有效方法,常被比喻为“最后的方法”,因为它可解决其他数值方法难以或不能解决的问题.鉴于此,本文系统探讨了Polya坛子模型与常见分布的关系,以便读者更深入理解与运用常见分布,如超几何分布与Polya分布,利用鞅论与随机模拟方法研究了Polya坛子模型,得出一些有趣的结论,这对其它概率模型分析提供了思路与方法,最后给出了随机模拟的MATLAB代码供读者参考.
1 Polya坛子模型与常见分布的关系
设坛子中有b个黑球,r个红球,每次随机取出一个球,取出后将原球放回,再加入c个同色球和d个异色球.记Bn为第n次取出的是黑球,Rn为第n次取出的是红球.[7]若连续从坛子中取出三个球,其中两个红球、一个黑球,则有
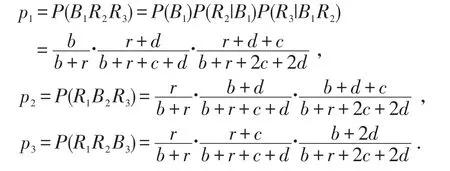
显然,以上概率与黑球在第几次被抽取有关.Polya坛子模型因抽样结果与抽样过程有关而难于理论分析.下面在特殊情况下,探讨Polya坛子模型的各种变化.
(1)当c=-1,d=0时,前次抽取结果会影响后次抽取结果,但抽取黑球概率不依赖抽取次序,这也是抽奖、抓阄的理论依据,即不放回抽样.

(2)当c=0,d=0时,即为放回抽样,前次抽取结果不会影响后次抽取结果.
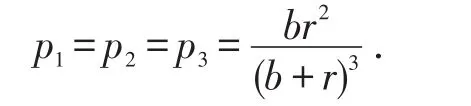
(3)当c>0,d=0时,每次取出球后,会增加下次取到同色球的概率,即每次发现一个传染病患者,都会增加以后再传染的概率,称为传染病模型.
显然,利用对等性有:此结论也可用数学归纳法很容易证明.
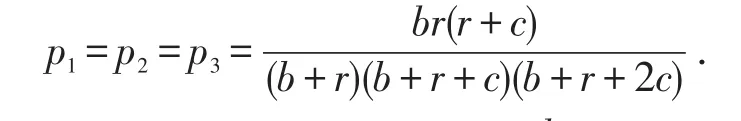
(4)当c=0,d>0时,称为安全模型,也称为Friedman罐子模型.即每当事故发生后,安全工作就该抓紧,下次再发生事故的概率就会减少;反之,则否.
当d=0时,假定进行n次抽样,令ξ表示n次中抽到黑球的次数,则

其中显然,这构成一概率分布,称为Polya分布.当c=-1时,Polya分布ξ就是在产品的质量控制中是常用的超几何分布.[1]
定理1当d=0时,令表示n次中抽到黑球的次数,则
证明 令表示第i次抽球中抽到黑球的个
数,则是同分布于B(1,p)而非独立的序列,显然, Eξi=np, Dξi=npq.于是,
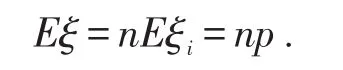
当 i<j时,

令如果对于保持常数,则Polya分布收敛于二项分布.如果并令采用数学归纳法很容易证明:[1]

其中,表示n次中抽到黑球等于k次的概率.该结论也可称为Polya分布ξ的负二项逼近.
现将Polya分布推广:如果一个离散型随机变量X的分布律为

其中 β,m>0,则称X服从参数为 β,m的Polya分布.当r≥1时,令d=βm代表传染数量, β代表相对传染,则
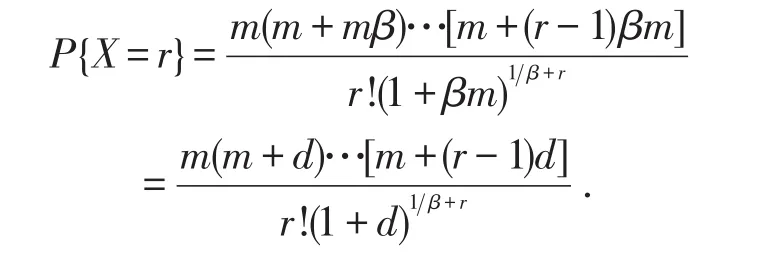
由 于其中因此推广Polya分布的分布列可改写为:

进一步有,分布函数
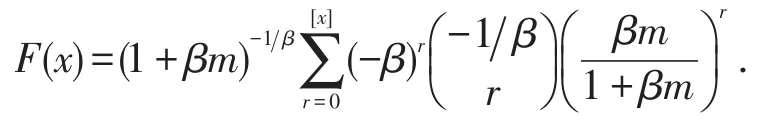
母函数
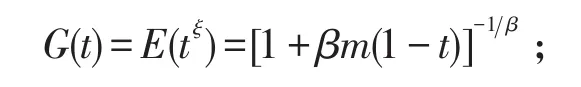
矩母函数

特征函数
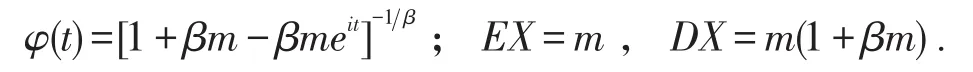
显然有:

即当时,Polya分布退化为泊松分布,因此Polya分布是泊松分布的连续修正.[2]
2 Polya坛子模型的鞅分析
定理2在Polya坛子模型中,当d=0时,令Mn表示第n次抽取后坛子中黑球的比例,则{Mn}是一致可积鞅存在,且
证明 令Xn表示第n次抽取后坛子中的黑球数,则是一个非齐次的马尔可夫链(MC),其转移概率为

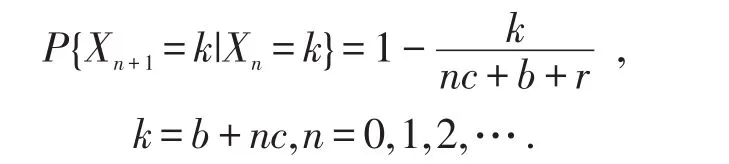
因为中对 Xn+1有影响的信息都包含在Xn中,所以
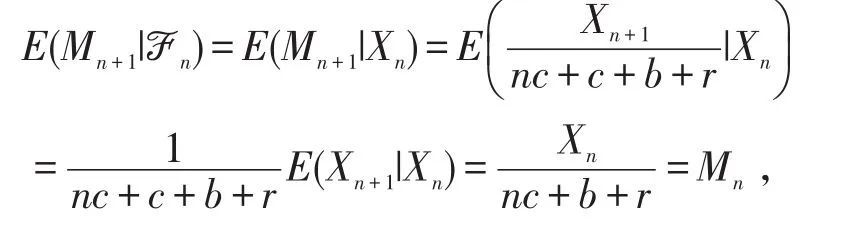
即{Mn}是一个鞅.又因为成立,所以{Mn}是一致可积鞅.
设0<a1<a2<1,Mn<a1且令
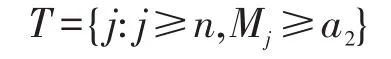
表示n次摸球后第一次比例从小于a1到超越a2的时刻.令Tm=min{T,m},则对于m>n,由停时定理可知但是

即因为上式对一切m>n成立,于是有这说明至少以概率红球的比例永远不会超过a2.同样的讨论可知红球的比
例从超过a2到再一次回到a1的最大概率为我们可知从a1出发超过a2,再小于a1,…,an有n个循环的概率应为可见,比例不会在a1,a2之间无限次跳跃,由a1,a2的任意性可知存在,记为 M∞.
因为{Mn}是一致可积鞅,故

证毕.
设事件A出现的概率为θ,为估计θ做了n次独立观察,其中A出现的次数X服从b(n,θ),即假如在试验前对事件A毫无所知,Bayes建议用均匀分布U(0,1)作为θ的先验分布.由贝叶斯公式可得θ的后验分布

这就是Be(x+1,n-x+1)分布.假如对坛子中的黑球的比例P一无所知,只能假定P服从U(0,1)(先验分布),而后验分布M∞是期望为的贝塔分布,进一步可得:M∞服从分布.特别当b=r=c=1,d=0时,M∞服从U(0,1)分布.相当于对坛子中的黑球的比例一无所知且没做试验.
3 随机模拟
对一般Polya坛子模型进行理论分析很困难,但可利用随机模拟方法对其仿真,进而从数值上探讨其性质.随机模拟方法提供了对复杂随机系统进行研究的一种思路,但在软件实现时,需要一定的技巧.随机模拟的编程实现是很多研究者的障碍之一,故下面给出Polya坛子模型的随机模拟程序供读者参考.
当b=6,,r=4,c=3,d=2,抽样次数n=10时,一共模拟m=100000次,MATLAB程序如下:clear all;c=3;d=2;n=10;m=10^5;%n:每次模拟的抽样次数,m:模拟次数

mp=m1./m %在n次抽样中黑球出现次数0到10的概率
m2=hist(bs,11);%利用hist命令统计黑球出现次数mp2=m2./m %当m较大时,mp2同mp
bnp=sum(bx)/m %第n次抽到黑球的概率
xb=[0:1:10];Eb=dot(xb,mp);Db=dot(xb.^2,mp)-Eb^2;
[Eb,Db] %由模拟分布列计算期望与方差
[mean(bs),var(bs)]%由模拟结果计算期望与方差
hist(bs) %模拟结果直方图
一次运行部分结果如下:
mp=0.0015; 0.0091; 0.0375; 0.0883; 0.1547;0.2065;0.2103;0.1614;0.0909;0.0334;0.0064 bnp=0.5261;ans=5.4840;3.1615
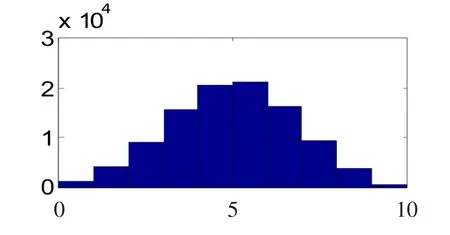
图1 10次抽样中黑球出现次数ξ的10000次模拟结果的直方图
这表明,当b=6,,r=4,c=3,d=2时,10次抽样中黑球出现次数ξ的分布列为

ξ取值012345678910概率0.00150.00910.03750.08830.15470.20650.21030.16140.09090.03340.0064
且5.4840,3.1615,第10次取出黑球的概率P(B10)=0.5216,100000次 ξ的观测值就是向量bs的取值,其直方图如图1所示.
上述结果很难通过理论分析求得,但通过随机模拟可得出数值解,非常有实际意义.
特别有,当b=6,r=4,c=3,d=0时,10次抽样中黑球出现次数ξ就是Polya分布,分布列的模拟结果如表1所示.计算Polya分布理论值的MATLAB程序如下:

end
lpb %Polya分布列的理论值
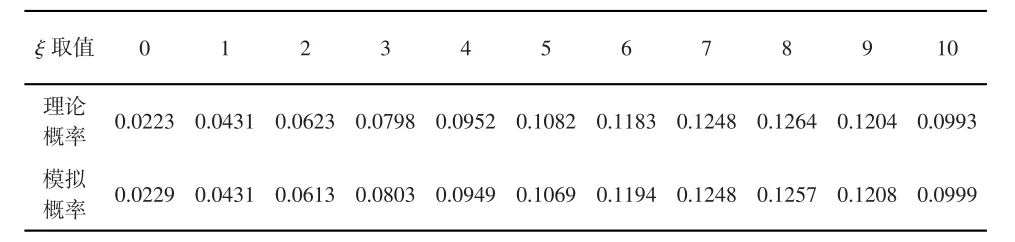
表1 Polya分布(b=6,r=4,c=3,n=10)的理论结果与模拟结果
第10次取出黑球的概率P(B10)的理论值为0.6,模拟值为0.5991,期望Eξ的理论值为6,模拟值为6.0030,方差 Dξ的理论值为7.3846,模拟值为7.4041.
由以上结果可知,模拟结果与真实值的误差较小,非常具有参考价值.随机模拟与理论分析的结果相互佐证,这也从侧面说明:模拟程序可行、准确,值得参考.如果需要考查Polya坛子模型的其它指标,只需对上述程序进行简单修改就可实现.
[1]董立华.波利亚(polya)分布[J].德州师专学报,1999,15(2):90-92.
[2]徐晓岭,王蓉华,顾苑培.Polya分布在气候统计中的应用[J].数理统计与管理,2008,27(2):215-226.
[3]努尔买买提斯吉,杨纪龙,米辉.关于罐子模型一个极限分布的注记[J].南京师范大学学报(工程技术版),2007,7(2):87-90.
[4]胡学平,姚劢.一个Pólya罐子模型的极限定理[J].安庆师范学院学报(自然科学版),2007,13(2):7-8.
[5]茆诗松,程依明,濮晓龙,编著.概率论与数理统计教程[M].北京:高等教育出版社,2004:40-45.
[6]王丙参,魏艳华,孙永辉.复合负二项风险模型的分布函数[J].统计与决策,2014,50(2):66-69.
[7]魏艳华,王丙参.蒙特卡洛积分及其改进[J].统计与决策,2017,53(12):71-73.
[8]张波,张景肖.应用随机过程[M].北京:清华大学出版社,2004:130-160.

