一年级学生代数学习情况测查与启示

陈 敏 王张妮

一、相关背景介绍

浙教版新思维小学《数学》在早期代数教学方面做了不少探索，其中有一项特色举措是：从一年级开始引入图形符号表示数，引导学生开展图形等式推算（如下图），进而利用图形等式来沟通各种数量关系，求解较复杂的应用问题。

图1

2016年暑假，由张天孝老师领衔，启动教材修订。2017年9月，修订后的一年级上册教材完稿，少量印刷，供部分实验学校志愿开展前期实验。同期，张老师还开始了《新思维儿童数学》系列学习材料的创作，目前《新思维儿童数学》1A册、1B册业已出版。在这些书中，我们发现，图形等式推算的相关内容得到了进一步梳理和充实，题型更丰富，序列更完善。

学习材料的价值最终应通过学生的学习效果来检验。刚入学的一年级学生能够理解这些图形等式的意思吗？理解到什么程度？他们是怎样解决这些问题的？有哪些共性？对我们的教学有什么启示？我们试图进行研究。

二、测试情况说明

2018年1月，我们选了两个试用一年级上册修订版教材的班级，进行了一次测试。其中一个为城市民办学校的教学班，生源较好，下文记为A班，样本数31人；另一个班级为普通公办学校的教学班，生源以外来务工人员子女居多，基础相对薄弱，下文记为B班，样本数35人。

图2 测试内容

三、测试结果分析

1.学生普遍能正确求取加减等式中缺失的数，“式=数”型近乎全对，“式=式”型略弱，亦达80%左右。

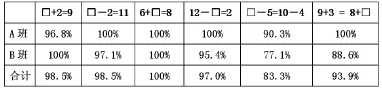
表1“求方框里的数”各题通过率一览表

我们认为：通过合理的教学，学生可以在起步阶段就较好地理解“=”的意义，不仅用于表示“运算得到……”，还能解读为“两边相等”，即“=”不仅是一种程序符号，也是一个关系符号。

式和式的相等，使情况变得相对复杂，使一部分学生略感困惑。但经过简单的访谈，发现它也激发了部分学生的高层次思维。如□-5=10-4，大部分学生的想法都是先算等式右边10－4=6，再想□-5=6，6+5=11。也有少数学生利用了差的变化规律“两边的差相等，5比 4多 1，□也比 10多 1，□=11”。

2.学生很容易接受图形符号表示未知数的观念，但进一步的推理过程尚未完全达到代数水平。

第2题（1）小题，学困生主要依靠直觉或者用试错的办法求取图形表示的数。通过对解答错误的三位学生访谈得知：

一位学生先基于计算经验，想出图形代表的数，再根据得数拼凑相应的算式，充作过程；

另一位学生对解题格式不太理解，但他也是正向思考的。

多数学生能够清晰地说明算式各部分之间的关系，如“一个加数=和－另一个加数”之类，并利用关系推算图形表示的数。但根据有关研究文章，这仍是算术思考，不能算代数思维。

而一年级学生特别不能把“式”凝聚成一个对象，不习惯“式”的代入和推理。第2题（2）的答题情况很能说明问题。

第2个方程组不能直接算出■或★等于多少，要用“■+■”替换★，将第2式转化成■+■－7=■，两边再同时消去1个■，变形成■－7=0，从而得到■=7，★=7+7=14。解决这个问题不能完全依靠数值的计算，更多是关系的推理，这道题发生错误或不会做的人数就大大增加了，在生源薄弱的学校尤其如此。

表2“求图形表示的数”各题错误率一览表

第3题，学生基于一定的计算经验，虽然能对图形所表示数的大小作出估计，但进一步的精确分析则显然存在问题。基于代数符号的关系推理对一年级新生来说是抽象的、有挑战的，不同生源的差异很大。

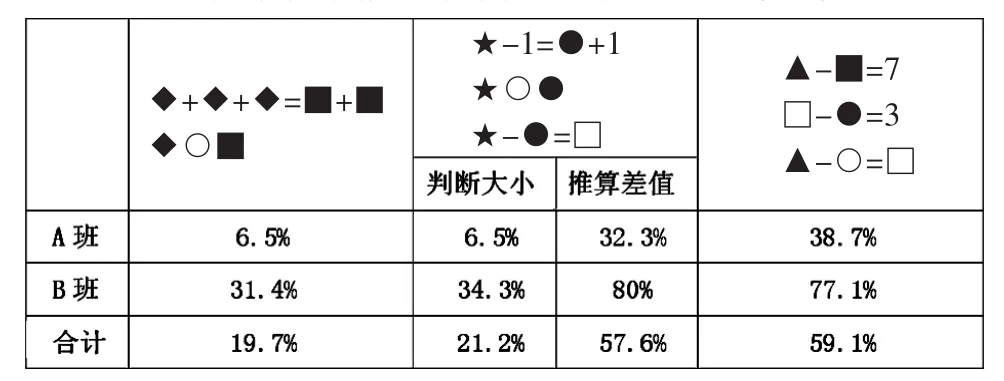
表3“根据所给信息推断大小”各题错误率一览表

第4题，根据已知信息，只能推断出不同玩具所表示的数之间的关系（和与差），而在限定的关系下，具体的数值有多种可能。数据表明，多数学生不是这样思考的，当关系推导的要求较高时，他们会退守到最初的直觉或试错水平。

表4“玩具分别表示几”两小题通过率比较

四、对教学的启示

学生的表现既给了我们开展早期代数教学的信心，同时也启发我们要根据不同学龄段的特点，采取合适的教学策略，将代数和算术的教学有机整合起来，更好地发展学生的思维。

1.初期教学从算术开始，重视借助直观，培养学生的逻辑推理能力。

早期代数不等于早教代数，更不是以代数思考去替代和取消算术的思路。我们倾向于认为算术是代数的必要基础。通过算术的学习，学生充分感知数的特性，积累运算的经验，对于进一步抽象的代数学习来说，是非常必要和有益的，且算术内容本身具有独特的思维训练价值。

在学生刚刚开始学习计算时，就引入图形等式推算，一方面在于帮助学生比较自然地接受用符号表示未知数的观念，将未知数和已知数同等看待，借助数值运算的经验去感知和理解代数运算的基本规则；另一方面，创造机会，让学生从单纯、单调的正向计算训练走向更为灵活的推理。

如学生要计算“10+2=？”，基本上就是执行了一个程序：十位不变，个位0+2，得12；而面对10+●=12，我们追求的是对图形等式有意义的理解和有逻辑的推理。建议的教学流程如下：

阶段一：从熟悉的情境中抽象出图形等式，依托情境意义完成推算。

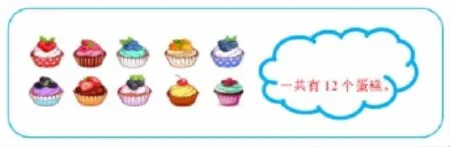
引导学生思考：吃掉的蛋糕+剩下10个=12个，吃掉的蛋糕个数不知道，用●表示，得到10+●=12。●怎么求呢？用总数（12个）－剩下的部分（10个）=吃掉的部分。●=12－10，●=2。

阶段二：将情境抽象成线段图，基于线段图开展图形等式推算。如：

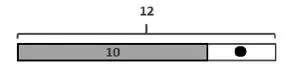
学生可以依据线段长度之间的关系，列写图形等式并完成推算。

阶段三：抽象的图形等式推算。学生可以根据自己的认知水平对图形等式做必要的解读。

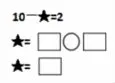
抽象水平较高的学生可以直接推算，抽象水平稍弱的学生也可以转化成相应的线段图或生活情境来帮助自己。

通过不同表征之间的相互转译和转化，希望学生真正理解图形符号的意义，理解其中部分和整体的关系，“超越熟练掌握计算和流利的计算，注意数学深层次的结构”。

“图形表示几”不是图形等式推算训练的重点，对各种基本数量关系的分析、比较、概括和推理是有价值的，即便这种思考还不完全是代数的。

2.设计“跳一跳”型任务，渗透代数思考的经验，开发学生学习的可能性。

在测试中，我们发现学生精通“数”的代入，但不太适应“式”的代入，而这种经验是可以去刺激和突破的。由于小学生以形象思维为主，我们可以创设直观情境，引导学生思考将下图右边天平中圆柱取走，天平会怎样？若想天平继续保持平衡，左盘里应再放入几个立方体？为什么？

多有几次类似经历，学生就能从1个数或1个量的代入进展到1组数或1组量的代入了。

另外，关于不定方程的解的问题，我们可以组织学生玩猜数游戏：不同的图形表示不同的数（自然数），●+▲=10，●和▲可能是几？根据学生的回答列成表格。请学生观察表格，说说自己发现了什么？强调●和▲的变化，更要强调它们之间不变的关系，即●+▲=10。

在此基础上，尝试下题（左边的数表示一行的和，下边的数表示一列的和。）

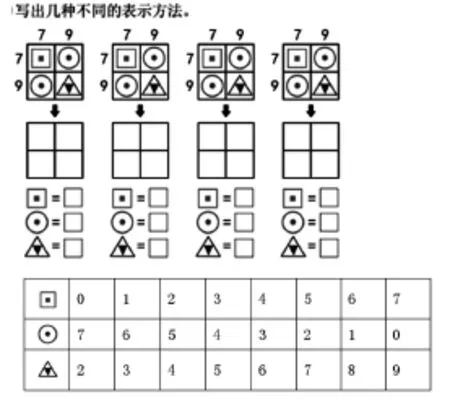
学生从盲目的试错，到自觉地分析：=7，而=9，所以一定比多2，逐渐地，学生就能跳脱1式、1数的点状思维，关注到两个数之间的关系，萌发函数观念。