基于FPGA的64QAM解调系统算法研究
殷志勇
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
正交振幅调制(QAM)是一种高效的利用载波幅度和相位联合调制的技术,因其极高的频谱利用率而被广泛应用于现代数字通信系统中。在高阶QAM数字通信系统中,因发送端和接收端的本地振荡器时钟不一致、信道的时变特性等原因,会导致接收端出现明显的相偏和频偏。这也是影响解调性能的最主要原因之一。解调恢复算法最主要的目的就是解决相偏和频偏问题。
本文主要研究了64QAM解调系统关键技术,包括载波恢复和位同步,提出适合高阶QAM数字解调系统的载波恢复算法,介绍了各个模块的设计方法和工作原理,完成各个算法模块的设计,实现解调系统的电路编程。
1 64QAM调制解调理论
1.1 QAM调制解调系统组成
正交振幅调制是利用已调信号在相同带宽内的频谱正交来实现2路并行的数据信息传输,其信道频带利用率与单边带调制一样,主要用于高速数据传输系统中。QAM系统组成框图如图1所示。

图1 调制解调系统组成框图
x1(t)和x2(t)是经过处理的独立带宽受限的基带波形,cosωct和sinωct是2个相互正交的载波。y1(t)和y2(t)是理想相干解调的结果。
在实际工程应用中,为了获得较高的频带利用率,通常采用高阶的QAM调制,本文具体讨论64QAM的调制解调,64QAM信号的基带波形取8种电平(±1、±3、±5、±7)。64QAM调制信号的信息传输方式为6 bit二进制。
1.2 星座映射
多电平正交调幅信号是一组在幅度与相位上都携带信息的载波键控信号,它可以用其复包络表示。多电平正交调幅信号的传输波形集相应于复平面上的矢量端点集,又叫做多电平正交调幅的星座图(Consetllation)。
根据相关文献[1],在4种映射逻辑(全平移对称型、全镜像对称型、平移/旋转对称型和镜像/旋转对称型)中,镜像/旋转对称型误码增值(由于逻辑变换和差分译码引起的误差扩散)最小,故采用镜像/旋转对称型作为64QAM调制信号星座图的逻辑映射方式,如图2所示。
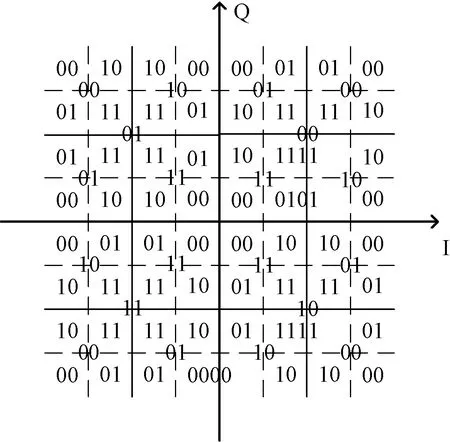
图2 镜像/旋转对称型逻辑映射
将复平面按格雷码编码进行3次切割,第2次以原点为轴进行每次π/2的旋转对称变换,第3次进行镜像对称变换,得到最后的64个符号点。图中,横坐标及纵坐标的取值均只有8种,且分别为±1、±3、±5、±7。每个符号点分别对应1组I、Q值,输出的同相、正交支路信号经过成型滤波,与正余弦信号相乘,完成调制。
2 载波恢复算法
QAM解调的核心是载波恢复算法,载波恢复算法一般都是基于锁相环技术,不同的是鉴相器的设计。实现载波同步有2种方法:传统的插入导频法因为发射功率的利用率下降已经被摒弃不用,应用较多的是基于锁相环的相干解调法。
载波恢复环路主要由以下4个模块构成:数控振荡器、成型滤波器(实现低通滤波功能)、鉴相器及环路滤波器。其中,鉴相器模块在程序运行一定时间会自动从极性判决算法转化为DD算法。在Vivado软件开发平台上利用Verilog HDL编写程序实现各模块算法。图3为FPGA实现时,载波恢复模块实现框图。

图3 载波恢复模块实现结构图
2.1 DD算法
DD算法利用星座图上的所有点进行判决,简单有效。缺点是:如果接收到的信号存在比较大的初始相位偏差,很容易出现参数判决错误点。一般只用在低阶QAM调制的载波恢复阶段。本文用在高阶64QAM载波恢复的跟踪模式。信号直接进行判决,与最近的星座点比较得到相位误差[2]。
输入信号为r(n),忽略噪声和一些其他情况,产生的相干解调信号为q(n),q(n)用复数形式表示为:
q(n)=rej(2πf1Ts+θ)=
r{cos(2πf1Ts+θ)+jsin(2πf1Ts+θ)}
(1)
q(n)经过逐电平判决,输出为:
(2)

(3)
这里符号的意思是判决后的输出结果,经过已经求出的门限值,判决到理想星座图上附近点,所以sgn[I(n)]和sgn[Q(n)]的值分别有±1、±3、±5、±7共8种情况。工程实际中,在FPGA中实现乘除法,一般通过移位实现。比如乘以7,相当于左移2位加左移1位加左移0位。左移相当于扩展,左移2位就扩展3位,最高位为符号位,中间为原数,低位补2个0 bit位。分母有2、10、18、26、34、50、58、74、98等情况,分别进行右移位计算。
2.2 极性判决算法
极性判决算法是多模式转换的算法,它的功率检测门限值有多个,在不同的模式下使用不同的门限值。系统运行开始,门限设置比较低,允许较多的符号通过,这样可以得到粗略的频偏[3]。根据实际情况,在系统运行一段时间后,再将门限值增高,这样可得到更精确的频偏。极性判决算法将信号判决到相应对角线上的点,利用初始门限值0,增大系统收敛速度,提高门限值,从而提高判决精确度。
星座图点用极坐标形式来表示可写成:

(4)
在第一象限中,假设极性判决检测器的输出对角线上的点为p(n),它的极坐标形式为:

(5)
其中:
(6)
θ(n)=arg[a(n)]+Θ(n)
(7)
A是大于零的常值,则若用鉴相器,可得到相差为:
(8)
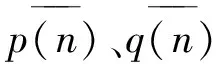
若a(n)属于对角线上的符号点之一,那么:
(9)

2.3 极性判决算法到DD算法的转换
根据时间转换模式设计自动转换模块。具体过程如下:在锁相环开始工作的时候,采用极性判决法,使用小的τ值进行相位误差检测,同时使用大的环路增益,这样可以有更多的星座点被用来提取相位信息,扩展环路捕捉范围;当环路粗锁后,将τ值调大,环路增益变小,此时相位检测的噪声小,环路的相位抖动下降,实现相位误差的精调。最后相位检测器切换到面向判决(DD)模式,利用所有的星座点进行稳定的相位误差纠正。这种模式的变换由自动模式机制来实现。自动转换机制在现场可编程门阵列(FPGA)中实际上就是一个以周期为单位的时间计数器,当计数器达到一定数值的时候,将DD算法的输出赋值给电路最终输出,得到结果。
2.4 模块实现
输入数字信号首先通过寄存器缓存,然后与数控振荡器输出的正余弦波相乘。数控振荡器在这里是调用Vivado中的直接数字频率合成器(DDS)知识产权(IP)核(见图4)。
设置滚降系数为0.35,利用Matlab中的函数生成与调制信号端结构完全相同的开平方升余弦滤波器的系数,将系数写进coe文件。调用Vivado中的有限冲激响应(FIR)IP核,将生成的coe系数文件导入。图5为生成的滤波器IP核。

图4 DDS输出结果

图5 开平方升余弦滤波器
3 位同步算法
载波恢复中,实际情况要在符号的最佳判决时刻进行判决。这就需要先完成定时恢复,提取位同步信号。位同步模块用于生成位定时信号,以便于DD算法符号判决时能在最佳采样点进行,图6为各个模块信号流程图。同步环路由数控振荡器模块、插值滤波器模块、定时误差检测等模块组成。
3.1 插值滤波模块
内插器可以实现数据数率转换,工程中常采用具有Farrow结构的立方插值器[4]。
由图7规定3条纵向支路分别为x1、x2、x3,横向支路为结果y(k)。则计算公式分别为:
x1= 0.5x(n)-0.5x(n-1)-
0.5x(n-2)+0.5x(n-3)
(10)
x2= -0.5x(n)+1.5x(n-1)+
0.5x(n-2)-0.5x(n-3)
(11)
x3=x(n-2)
(12)
(13)
这种插值器1个周期内需要4个采样点。在FPGA中,用信号传输速率4倍的时钟作为采样信号,即可实现。
3.2 误差检测模块


图8 误差检测器原理图
64QAM调制信号如果要用Gardner的算法,要对其进行稍微的改进。还是上面的例子,符号1变为3,平均值是2,相当于横坐标上移2,即上移了a=[yI(k)+yI(k-1)]/2。所以,对于64QAM信号而言,Gardner误差检测算法的公式为:
(14)
3.3 数控振荡模块
NCO在适当的时候产生需要的内插点。这里的NCO是一个相位递减器,利用算法实现。差分方程为:
η(m+1)=[η(m)-ω(m)]
(15)
式中:η(m+1)为第m+1个时钟的NCO寄存器值;ω(m)为NCO的控制字。
若η(m)-ω(m)≥0时,值不变;当η(m)-ω(m)<0时,η(m+1)=[η(m)-ω(m)]+1。保证NCO寄存器值一直都是正小数。ω(m)为环路滤波器的输出值。NCO寄存器随时间的变化关系如图9所示[4]。

图9 NCO寄存器时间关系
图9中,mkTs是采样时钟脉冲点,第k个插值时刻kTi=(mk+μk)Ts,为NCO寄存器溢出时刻。由相似三角形原理可得:
(16)
本文所讨论的算法中,ω(mk)=0.5时,环路正好达到平衡。
3.4 算法仿真
在Matlab中进行仿真,设置符号速率为Rb=30 Mbps,成型滤波器滚降因子α=0.35,采样频率fs=4Rb=120 MHz。符号数50 000个,环路滤波器输出初始寄存器值ω(mk)=0.5,NCO寄存器初始值η(mk)=0.7,NCO初始输出定时分数间隔器μk=0.6。得到如图10所示的结果。

图10 位同步算法仿真结果
4 系统测试
在Matlab中生成50 000个64进制的随机数,转化成6 bit的二进制数,将每组数的最高位和第2位进行差分编码。编码后的数按误码增值最小的“镜像/旋转对称型逻辑映射”映射为同相正交数据,绘制星座图。图11为初始星座图。设置采样频率Fs=210 MHz,码速率ps=30 Mbps,Fs/ps为内插因子,分别对同相正交支路升采样,开平方根升余弦滤波器滚降系数为0.35,载波频率70 MHz。将同相正交支路信号相加,生成64QAM已调信号。波形如图12所示。

图11 初始星座图
DD算法载波环路需要获取到位定时信号,且只有获取到正确的位定时信号的前提下,环路才能正常锁定[5]。Gardner位同步环路可以在载波相位未同步的情况下完成锁定,位同步信号sync作为DD算法鉴相模块的输入信号。完成模块关联,读取64QAM已调信号的txt文件,实现载波恢复。时钟周期为4.7 ns(210 MHz),仿真时间单位为ns级,在400个时钟周期后复位信号从高电平1变为低电平0,系统开始工作。图13为系统解调结果。
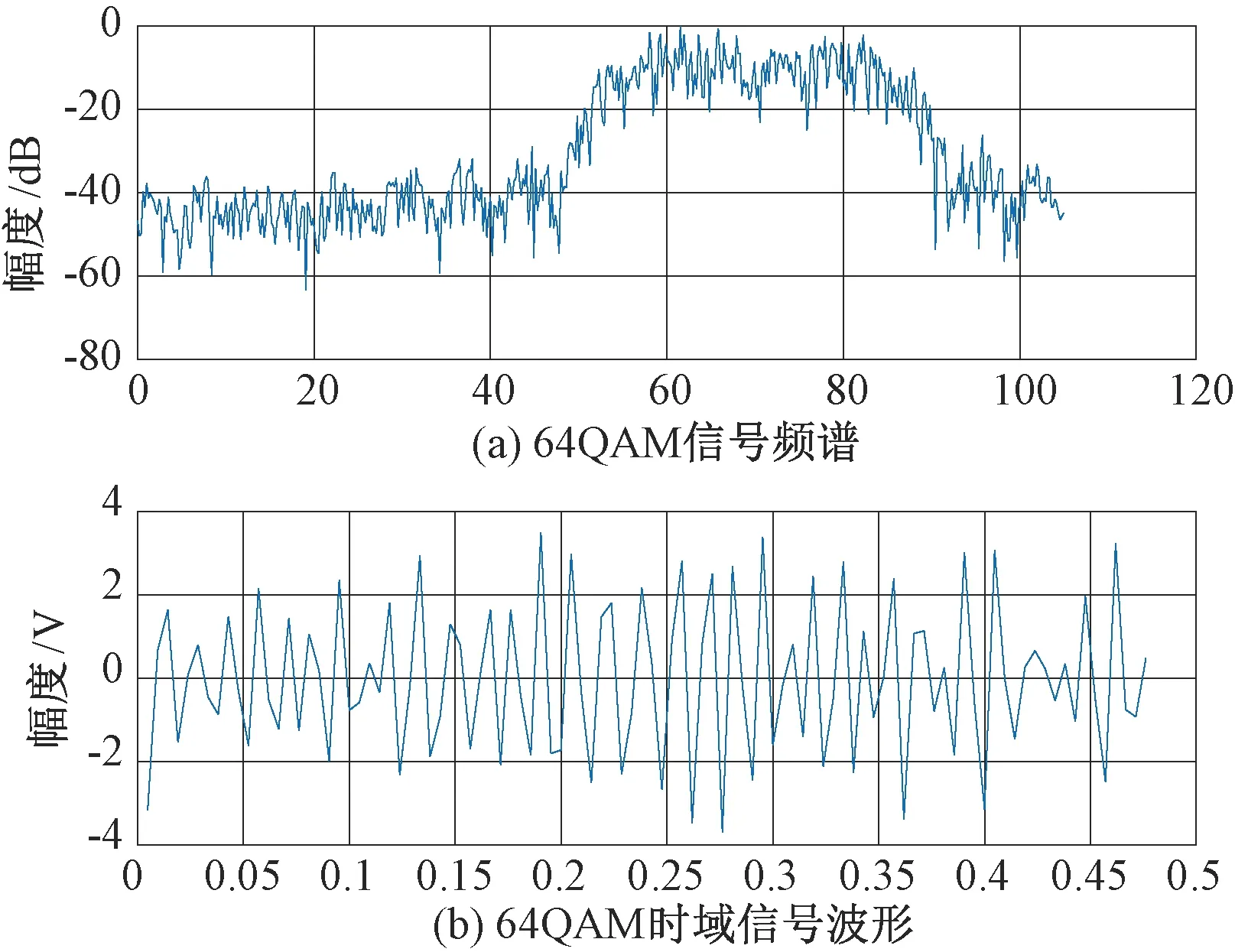
图12 原始64QAM已调信号波形

图13 系统解调结果
载波恢复的结果比较理想,在仿真时间14 000 ns时,环路完成锁定,稳态相差基本不变,没有比较明显的波动。位同步模块中分数间隔很快能保持稳定,定时误差信号在零值附近很小波动。将最后的I、Q路信号写入txt文件中,在Matlab中调用,绘制星座图,得到图14。
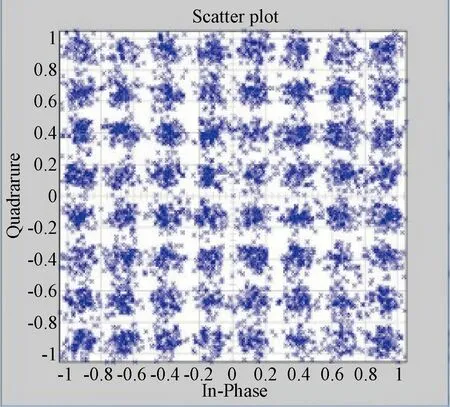
图14 载波恢复星座图
5 结束语
本文对64QAM载波恢复算法进行分析,并且对位同步算法实施仿真,在Vivado中设计各个模块的FPGA可实现电路。经过系统测试,结果说明基本能实现载波恢复,具有很小的稳态相差。波形结果和星座图的恢复,表明64QAM已调信号顺利实现解调,进一步证明了论文所设计的系统的正确性。
[1] 姚彦.多电平正交调幅的集映射与差分编码[J].电信科学,1987(7):28-30.
[2] 胡楠.高阶QAM数字快速解调及电路设计[D].成都:电子科技大学,2008.
[3] 夏文娟.基于高阶QAM的载波恢复方法的研究与实现[D].合肥:合肥工业大学,2013.
[4] 杜勇.数字调制解调技术的MATLAB与FGPA实现[M].北京:电子工业出版社,2015.
[5] WANG P,FAN P Z.New carrier recovery method for 16-QAM system based on full constellation points[J].Journal of Southwest Jiaotong University(English Edition),2007(3):187-191.

