基于测向数据多层预处理和多项式拟合的单站无源定位算法
赵 悦,尹俊平,姬利海,王妙妙,3
(1.东北师范大学,吉林 长春 130024;2.北京应用物理与计算数学研究所,北京 100088;3.北京工业大学,北京 100190)
0 引 言
当前,随着电子技术的日新月异,电磁环境日益复杂,电磁信号密集交叠。雷达是信息化战场和武器系统中目标信息获取、指挥控制、精确制导和火力打击作战体系中最重要的装备,也是取得信息优势的最重要手段。雷达对抗作为电磁空间斗争的主要作战手段,正朝着精确化、智能化方向发展,以应对现代战争的作战需求。精确化、智能化雷达对抗需要更加完整、准确、精细的侦察数据处理算法作为支撑。雷达对抗单站无源定位是侦察数据情报处理的重要内容之一,其具有仅用单套侦察设备、作用距离远、隐蔽性好等诸多优点。因此,单站无源定位一直是雷达对抗情报处理领域研究的热点问题。传统的有源定位技术是根据有源辐射来对目标进行定位,但其弊端是自身位置信息易暴露,同时容易受到电子干扰与对抗[1]。而无源定位技术可解决这一问题,其本身不主动发射对目标照射的电磁波,只需一定传感器和单个观测平台,设备简单、定位距离远且机动性良好,可快速实现对目标的定位[2]。
无源定位根据观测站数量不同可分为单站和多站定位2类,依据观测站状态又可分为固定站和运动站。为了准确地定位,多站定位系统对站间的协调配合要求比较高,实际操作过程中实现高精度定位非常困难。而单站无源交叉定位技术是利用一个运动观测平台对目标进行定位的技术。其实现过程是:单个运动观测站对辐射源进行连续测量,观测站运动到不同位置对应于目标不同的到达角,根据交叉定位方法,多条定位射线交汇的目标点即为定位结果[3]。利用单站在不同时刻的测量数据直接进行交叉定位的算法简单,但是定位结果不是最优[4]。传统非线性滤波算法中扩展卡尔曼滤波及其衍生算法的缺点主要是非线性误差导致滤波器性能不稳定,容易发散[5]。另一种常用的定位算法是最小二乘定位算法,该算法首先交叉定位得到目标的初始位置,其次对初始位置采用牛顿迭代法得到更精确的目标位置,很大程度上提高了定位精度[6-7]和定位效率。文献[8]~[9]给出了对定位精度进行分析的原理。文献[10]中仅对原数据进行分片处理及局部拟合,简单的数学平均和仅采用线性拟合并没有消除异常点对定位结果的影响。从数理统计角度,显然对数据的预处理,在一定程度上可避免某些异常点对定位结果的影响,提高定位准确度。鉴于此,本文采取先对测向数据进行多层预处理,再利用最小二乘定位算法进行定位的算法,该算法包含了去除明显异常、近邻相差小、超过容差的数据等多层预处理过程以及多项式拟合提取数据算法,从定位精度可以看出该算法可明显消除异常点对定位精度的影响。
本文内容主要分为两大部分:第一部分为测向数据多层预处理和多项式拟合算法、最小二乘定位算法以及几何精度分析原理;第二部分是数值实验,对模拟数据进行预处理、拟合、定位的计算结果以及定位算法的几何精度分析。
由表3能够直观地看出单个指标的得分情况,而结合表4两个因子的累计方差贡献率,进一步对每个指标进行加权汇总,能够推出每个因子的总得分公式:
1 基于测向数据预处理的最小二乘定位算法
1.1 初步判定
为了得到更精确的目标定位结果,首先基于脉冲数据特征进行一些初步判定。由于脉冲个数太少或方位角偏移角度较小,可能会导致定位偏差较大,所以进行如下判定:
(1) 考虑到数据容差、设备测量精度等原因,需借助最小二乘进行定位结果的优化,进而实现定位精度的提升。若脉冲个数较少,最小二乘定位方法的优势无法体现。所以我们考虑脉冲个数需大于某个设定值(例如10)时,才有较准确的定位结果输出。
《了不起的盖茨比》是被誉为爵士乐时代的“编年史家”和“桂冠诗人”的美国作家司各特·菲茨杰拉德的杰作,反映了美国社会转型期普遍存在的精神生态危机问题。深刻理解菲茨杰拉德对社会转型期出现的意识形态领域问题的思考及他对消费主义文化价值观所持的批判态度,对解决我国当今社会转型期存在的诸多精神生态危机问题具有一定的指导意义。
式中:σx、σy分别为x、y方向上的定位标准差。
1.2 预处理
1.2.1 删除考虑范围外的数据
供分析测试的少穗竹和四季竹竹笋均取自华安竹种园,各竹种分别采集大小适中,无病虫害和机械损伤,无明显空洞,无畸形,不干缩,生长健壮、鲜活的竹笋。剥除笋箨洗净后,纵切竹笋,采用四分法取样,分别取样测定含水量;其余置于60~70 ℃烘箱中烘干,粉碎并过0.5 mm筛后,保存于干燥器中,供其他成分测定使用。
经过初步判定后,先对超出考虑范围的数据进行删除,排除这些数据对定位结果的影响。例如考虑区间[0°,360°],对超出此区间的方位角进行删除。图1和图2为处理前后的对比图(这里采用下文仿真一中的数据进行预处理)。
(1)NFC手机支付今后将主要采用卡模拟技术,具体形式为使用“手机PAY-升级版ODA”方案或者“手机APP-HCE技术-token授信”方案,绑定银行卡并加载城轨行业应用信息,进出站脱机支付。NFC手机支付可完善银行卡在城轨的受理环境,避免银行卡换卡、电子现金在特定设备上圈存余额等问题。
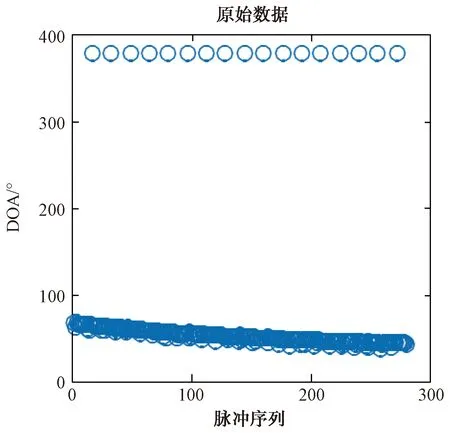
图1 删除前的脉冲序列

图2 删除后的脉冲序列
1.2.2 去除重复数据
剔除区间外数据后,再对短时间内相同或近邻相差较小的方位角数据进行去重复,尽可能地避免重复计算带来的误差。图3和图4为处理前后的对比图。

图3 去除重复数据前的脉冲序列

图4 去除重复数据后的脉冲序列
1.2.3 去除容差外的数据
没多久,市里要建一个新电厂,公开招工人。李红怂恿齐海峰和她一起考:“这可是个千载难逢的好机会,难道你要在菜站当一辈子临时工?万一哪天菜站解散了怎么办?”

图5 去除容差外数据前的脉冲序列
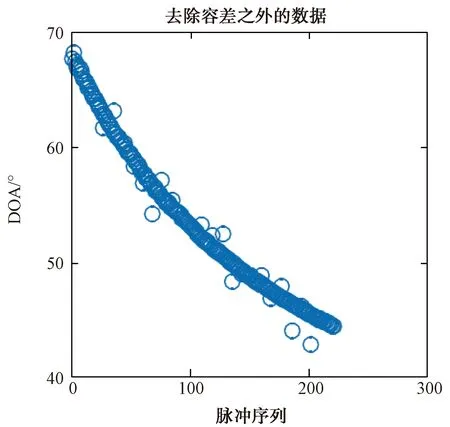
图6 去除容差外数据后的脉冲序列
1.3 拟合提取
通过多项式拟合曲线从上述处理后的数据中挑出满足一定规律的点。将拟合曲线与数据曲线相近的数据进行提取,再利用提取的数据进行定位。图5和图6为拟合曲线提取的前后对比图。

图7 拟合曲线提取前的脉冲序列

图8 拟合曲线提取后的脉冲序列
1.4 最小二乘交叉定位
现用不同时刻飞机的N个位置对目标A(xm,ym)测向,设飞机的N个位置为(xi,yi),根据三角关系有:
(1)

由以上等式可以推出GDOP为:
(2)

从而有:
(3)

H=FL+C
(4)
L的最小二乘估计为:
(5)
迭代方程为:
(6)

我在谷歌上填了她女儿的名字和学校,试着按下回车,没想到真的找到一个有关她女儿的帖子。那是一个山区老师发的,说他们学校条件很差,但仍有许多三好学生。帖子的最后,附了一张照片,几个孩子围着一个年轻的老师。万姐忽然指着蹲在前排的一个女孩儿说:“那是小洁,我女儿,都是三好学生了!”
把测向交叉定位结果取平均作为迭代初值,当误差达到设定的阈值时,迭代停止,输出定位结果。
1.5 几何精度因子(GDOP)分析
两站交叉定位是常用的定位方法,这里对单站两点交叉定位进行GDOP分析。
定位精度GDOP的定义式为:
(7)
(2) 在利用交叉定位时,若方位角偏移δθ=θ1-θ2非常小,则会导致tanθ1-tanθ2趋于0,进而引起定位误差偏大,无法定位。因此,当方位角偏移角度大于某个阈值时,方可进行定位。
对θi求微分得到:
(8)
式中:(xi,yi)分别为观测站的坐标;(x,y)为目标的位置坐标。
②构件1(第一层)对6个地震记录的损坏程度,即刚度折减75%和50%,相当于活性水平0.25和0.50(12 个情况);
令:
(9)
欧阳修说:“立身以立学为先,立学以读书为本。”书是良药,刘向说:“书犹药也,善读可以医愚。”书是益友,臧克家说:“读过一本书,像交了一位益友。”书是窗户,高尔基说:“每一本书,都在我面前打开了一扇窗户。”书是一艘船,它载着人们在知识的海洋中航行;书是一架梯子,它能引导我们登上知识的殿堂;书是一把钥匙,它能帮助我们开启心灵的智慧之窗。
中国是“竹文化”的发源地,竹编工艺是一门传统的中国手工艺术,历史悠久,被列入世界非物质文化遗产名录,不仅有极高的艺术价值,也是传统文化的传承。本文利用现有的研究成果,以区域作为划分依据和研究单位,对中国不同区域的竹编工艺进行分析研究,总结出中国不同区域竹编工艺文化的特点。结合当今的传统文化继承现状,思考如何将传统的竹编工艺文化与时俱进地融入现代生活中,面对现代潮流的冲击,如何更好地传承与发展。
MdX=Rdθ+P1dt1+P2dt2
(10)
当M可逆时,令N=M-1。设定测量误差为零均值,且站址误差之间是不相关的,可得到目标位置估计误差的协方差为:
E(dXdXT)=N(RE(dθdθT)+P1E(dt1dt1T)P1T+
P2E(dt2dt2T)P2T)NT
(11)
其中:
物性封闭圈闭又称成岩圈闭,指各种次生成岩作用使原始沉积的岩层孔隙性发生变化形成的圈闭[7-8]。其包括两种情况:一是由于胶结作用导致渗透层上倾部位孔隙度及渗透率降低,因渗透层上倾方向物性变差形成遮挡条件;二是由于次生变化,如白云岩化,使原来不具有渗透性的岩层一部分孔隙度、渗透率增大,形成低渗透层中的高孔、高渗段。
(12)
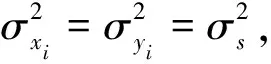
(13)
目标的位置误差协方差阵又可以表达为:
故上式可以转化为:
(14)
二是市场自主力量相对薄弱。市场主体数量和民营经济水平对市场力量影响至关重要。2017年大连全市私营企业总数约20.5万户,个体工商户总量达到42.6万户 [5]。相比较,深圳私营企业总数超过180万户,个体工商户也超过了130万户 [6],而且深圳高科技企业80%以上是民营企业 [7],因此深圳的市场力量才能强大,市场机制才能健全。大连还需要多增加民营企业数量,多培育高科技高成长性民营龙头企业。此外,大连企业市场化自主决策能力不强。央企、国企的公司管理现代化水平不高,过度依赖领导者喜好来配置人事、生产和销售资源。民营企业也缺乏真正独立性,存在一定的政商依附关系。
(15)
由E(dXdXT)的表达式可以求出GDOP值,并进行分析。
短时间内,目标方位角具有一定的稳定性,对于分段区间内破坏这种稳定性的异常数据进行删除。去除超出容差范围的方位角数据,尽量减少容差外数据的影响,提高定位精度。图5和图6为处理前后的对比图。
2 算法仿真
2.1 定位仿真
仿真1:设定目标经纬度为(121°E,38°N),飞机航迹的起始点为(121.4135°E,39.0142°N),飞机航迹的终点为(122.6102°E,39.5749°N)。起始点方向角θ1=67.82°,终点方向角θ2=44.42°。飞机从起始点向航迹终点飞行,在航迹上等间隔取160个测量点,通过仿真程序添加一些异常点数据,共计280 个数据点。表1是对各处理阶段数据的定位结果。
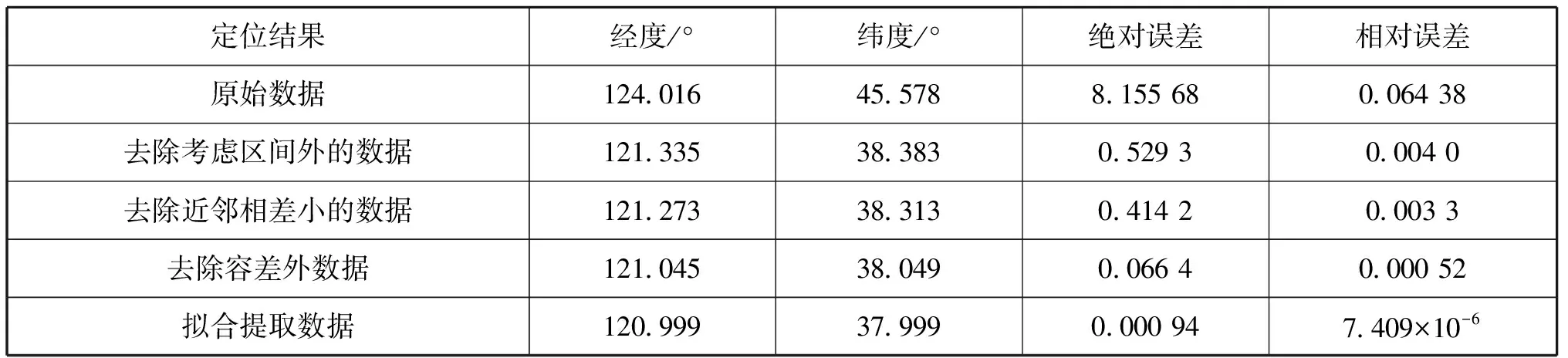
表1 仿真1中对各处理阶段数据的定位结果
以去除考虑区间外的测向数据作为基准,将去除近邻相差小、去除容差外、拟合提取的数据的定位精度分别与该基准的精度比较得到结论:定位的精度经此3个步骤分别提升了18.68%、86.97%、99.82%。
仿真2:设定目标经纬度为(113°E,35°N),飞机航迹的起始点为(116.353 1°E,40.043 1°N),飞机航迹的终点为(115.100 8°E,40.4135°N)。起始点方向角θ1=56.38°,终点方向角θ2=68.75°。飞机从起始点向航迹终点飞行,在航迹上等间隔取160个测量点,通过仿真程序添加一些异常点数据,共计279 个数据点。表2是对各处理阶段数据的定位结果。

表2 仿真2中对各处理阶段数据的定位结果
再次以去除考虑区间外的数据作为基准,将去除近邻相差小、去除容差外、拟合提取的数据的定位精度分别与该基准的精度比较得到结论:定位的精度经此3个步骤分别提升了4.15%、90.14%、99.77%。
鸡痘是由鸡痘病毒感染产生的,鸡痘病毒通常会存在于年末或者皮肤的病灶之中,对于自然环境具有相当强的抗性。无论是阳光照射、干燥还是低温环境,都可以存活很久。鸡痘病毒对于火碱水和醋酸水都很敏感,养殖常用的消毒药也具备一定的效果。
由上2个仿真结果表明,原始包含异常点的数据,经过上述3个步骤的预处理,定位精度得到大幅度提升。
2.2 定位精度GDOP仿真
设定2个观测点位置,观测点1的位置坐标为(0 km,0 km),观测点2的位置坐标为(60 km,0 km),目标与观测点1构成的方向角为θ1=40°,目标与观测站2构成的方向角为θ2=70°。考虑的仿真区域:X轴方向为±400 km,Y轴方向为±400 km。仿真不同站址误差和测向误差影响下的定位精度如图9~图11所示。
仿真1:测角误差为3 mrad,站址误差为1 m,GDOP分布图如图9所示。
黄酮类化合物母核中具有2-苯基色原酮结构,该类化合物种类繁多,在植物体内多与糖结合以苷的形式存在,是柳属植物主要的活性成分之一。柳属植物中共分离得到61个黄酮,其中有5种为从该属植物中分离得到的新化合物,具体化合物名称见表1[2-21]。

图9 GDOP分布图
仿真2:测角误差为3 mrad,站址误差为10 m,GDOP分布图如图10所示。
仿真3:测角误差为7 mrad,站址误差为10 m,GDOP分布图如图11所示。

图11 GDOP分布图
由图可以看出,定位精度受到站址误差和测角误差的影响,随着它们的增大,定位误差增大,定位精度下降。观察仿真1和仿真2的GDOP图得到:虽然定位精度随站址误差的增大有所下降,但站址误差变化对定位精度影响相对较小。而由仿真2和仿真3的GDOP图可知,测角误差的变化对定位精度影响较大。测角误差对定位误差的影响起主要的作用。图中标记点是目标真实位置的坐标,由仿真图可以看出,在800 km×800 km的区域内,目标真实位置所在区域的定位误差最小,并且目标在近距离内,定位误差较小,精度较高;在远距离时,定位误差较大。
3 结束语
本文主要针对单站无源定位算法进行改进,首先对测向数据进行多层预处理和多项式拟合,得到较纯净的测向数据,再利用直接交叉定位算法得到目标位置的初始估计,进而基于最小二乘及牛顿迭代得到更精确的目标位置。通过2组定位仿真,验证在采用多层预处理和多项式拟合后的数据进行定位时,定位精度分别提升了99.77%、99.82%。通过定位精度分析可知,测角误差对定位误差的影响显著,而站址误差对定位误差影响较弱。这些结论对进一步提高单站无源定位的精度具有一定的借鉴意义。
[1] 孙仲康,郭福成,冯道旺.单站无源定位跟踪技术[M].北京:国防工业出版社,2008.
[2] TEAK L S.Observability of target tracking with bearing only measurement[J].IEEE Transactions on Aerospace and Electronic Systems,1996,32(4):211-215.
[3] 汪珺.测向交叉定位技术[J].电子科技,2011,24(7):129-132.
[4] WILSON J.Precision location and identification:a revolution in threat warning and situational awareness[J].Journal of Electronic Defense,1999,22(11):43-48.
[5] 黄耀光,高博,李建新.基于平方根UKF双向滤波的单站无源定位算法[J].数据采集与处理,2013,28(2):207-212.
[6] 何青益,赵地.基于最小二乘方法的单机测向定位算法[J].舰船电子对抗,2013,36(1):37-39.
[7] 吕晶晶,姚金杰.基于最小二乘和牛顿迭代法的空中目标定位[J].微电子学与计算机,2011,28(9):108-110.
[8] 王好同,马钰,李伟明.无源测距定位系统设计中的GDOP分析[J].信号处理,2012,28(1):124-129.
[9] 赵琨,何青益.基于GDOP的三站时差定位精度分析[J].无线电工程,2012,42(5):15-17.
[10] 王超,于悦.运动干涉仪平台上单站无源定位算法研究[J].现代电子技术,2014,37(12):59-62.

