Ising模型在金融市场价格构成中的应用

栾玉国，贾泽正,李东海，付天宇(沈阳航空航天大学.理学院，.航空航天工程学部(院)，沈阳 110136)

随着现代技术的发展，特别是互联网技术推动全球化的深入发展，世界各国之间金融市场的发展非常迅速而深入。不断出现的金融风险和危机表明我们对金融系统复杂性形成机制的认识还不能使我们充分理解金融活动和管控金融风险，需要从原理和微观层面上研究金融市场的特性。近年来，由于计算机的快速发展，把金融市场看成是非线性统计动力学系统，利用理论物理知识和各种物理模型如Ising模型等来研究金融系统的价格形成机制和市场特性已经成为新的研究热点[1-4]。

Ising模型是利用粒子之间相互作用描述铁磁体的磁性及相变的随机模型，其中粒子自旋可以选择向上或向下[5-10]。简化的市场交易者在市场交易中则是一买一卖，粒子自旋和交易者这两者在行为上具有相似性。同时，比较金融价格形成和铁磁体的磁化强度，以及市场价格的突变和铁磁性的临界磁性相变等，也可看出它们都具有相似的复杂系统性质。应用Ising模型研究金融市场，可以通过简单的模型来研究和解释金融市场的行为[11-14]。本文主要分析中国金融市场中单个股票的价格行为，通过Ising模型模拟其价格曲线，研究其收益率时间序列和统计性质，并和A股市场的股指波动行为进行比较，了解个股价格行为的主要特点。研究结果表明，个股的收益率尖峰厚尾特征和A股上证指数相似，但概率密度函数分布更不均匀。

1 简化的Sznajd伊辛模型

Ising模型在经济市场中的应用，是将一维或二维格点上的N*N个自旋粒子看成投资人，粒子自旋Si(i,j=1,2,3，…,N2)的量子化取向只有朝上(Si=1)和朝下(Si=-1)，分别对应投资人的买进和卖出。在每一定步长的离散交易时间里 , 投资人有买进和卖出两个选项。每个投资人的交易决策，和相邻格点上的投资人投资取向以及投资舆论环境有关，以一定的概率形成自己下一步的交易取向，系统的哈密顿量如式(1)所示。

(1)

式中是对格点(i,j)的所有相邻格点上投资人交易取向进行求和，B代表舆论对投资人的影响。

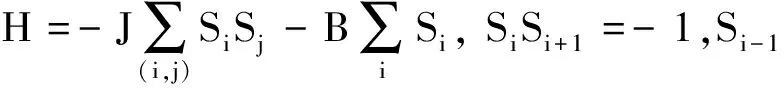
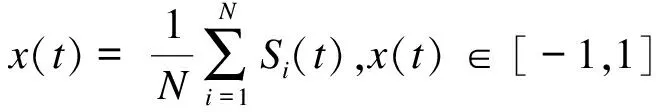
(2)

式中系统的价格x(t)会随着时间的变化而变化，当x(t)>0时，智者的交易选择为买进，反之则卖出。

根据以上所给的Sznajd简化的Ising模型，我们可以通过数值模拟的方式，给出价格曲线随时间的变化，并由此计算其收益率，通过与A股市场中的个股收益率的统计规律等进行比对研究，分析Sznajd模型描述价格产生机制和中国股市里个股的收益率的统计规律是否一致。模拟方法主要取20 000个格点，通过随机数产生其初始状态，根据蒙特卡罗方法按照Sznajd给出的规则进行演化。模拟按照中国股市的交易时间，每半个小时采集一组数据，共产生1 000个交易日的模拟价格曲线。图1为模拟得到的一组价格曲线。

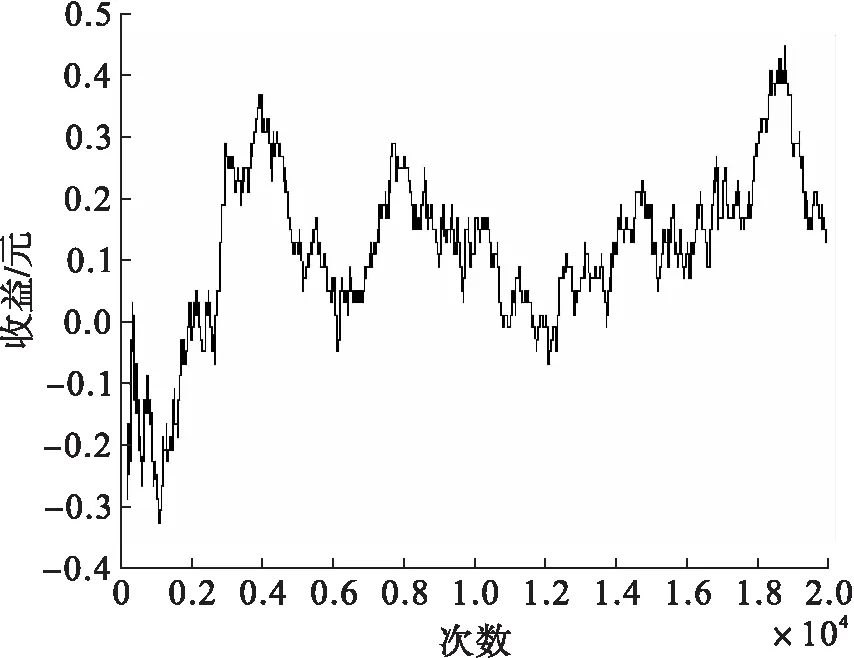
图1 Sznajd模型模拟股票的价格走势

模拟数据的相对收益率r(t)可以如公式(3)所示。

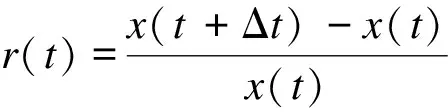
(3)

图2(横坐标表示模拟进行天数，纵坐标表示相对收益率，其值在-2～1.5之间)为上面模拟价格曲线对应的日收益率曲线。

2 模型结果和实际个股的分析比较

为和模型数据比较我们选取了一组A股市场的个股，计算了它们的相对收益率。在统计性质上，这些个股的相对收益率和概率密度统计特性比较相似，因此这里主要就给出一支股票平安银行(000001)，来和模拟数据进行比较分析。图 3是平安银行从2014年8月22日到2016年5月13日的价格曲线，其对应的相对收益率曲线如图 4所示。由上面给出的实际平安银行数据和模拟数据走势图我们进行线性回归分析和比较，给出图 5和图 6，可以看出在拟合线的上方，模拟数据的分布和实际个股的情况相当接近，都密集地分布于拟合线附近，表明模拟数据能够很好地模拟实际市场。

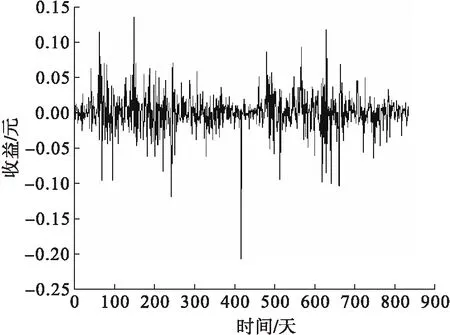
图2 模拟数据相对收益率曲线

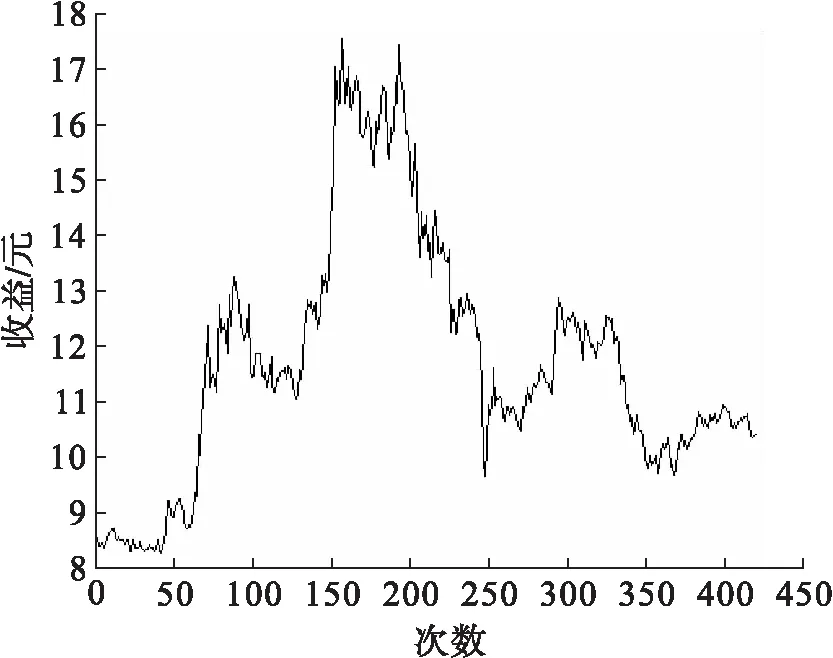
图3 平安银行股票的股价分布

同时，从模拟数据和实际数据的比较中，我们还看出，真实的市场中个股上涨和下跌的幅度和频次并不完全对称，小幅度上涨出现的概率很高，大幅上涨的数据很少出现，而大幅下跌的情况却并不少见。在图6的下方，可以明显地看到实际股票的开盘-收盘数据中，有少量数据大幅偏离拟合线，这些数据往往都是当天股价大幅下跌甚至跌停所导致。个股频繁的大幅下跌甚至跌停，实际上是市场恐慌情绪下的一种极端从众心理导致的非理性价格现象。这种现象在单个的个股中表现更为突出，甚至超过模型假定的范围，而在上证指数等综合指数中出现这种单日极端行情的情况相对较小，因此和模型模拟数据更加接近。

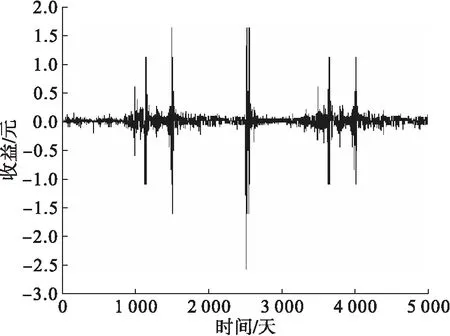
图4 平安银行股价相对收益率分布

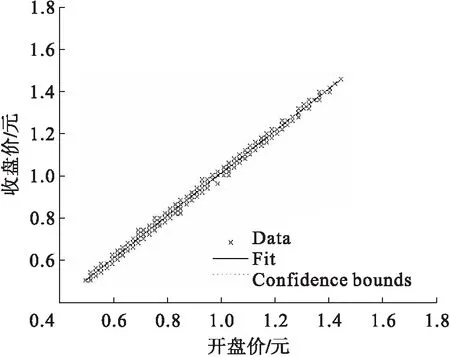
图5 Sznajd模型模拟证券的价格线性回归曲线

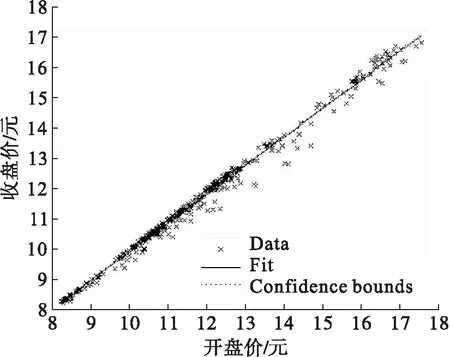
图6 平安银行股票价格的线性回归曲线

图7和图8是根据平安银行股票数据和模拟数据绘制的频率直方图，并分别叠加了基于回归分析给出的正态分布密度曲线。从图中可以看出模拟数据和个股的实际收益率样本在均值附近直方图的数值都明显地高于正态分布曲线，尾部也要高出密度曲线，具有明显的尖峰厚尾特点[15-16]。但平安银行证券实际收益率数据明显具有不对称特点，如负收益率的部分出现低频大数值现象要比对应的正收益率部分高，而模拟数据的频率直方图分布更加对称。

这一现象表明投资人在证券市场上，同样的收益率大小，不同的方向上交易偏好存在差异。在Sznajd模型中，这种交易偏好差异仅仅给出投资人买卖的简化假设，对正负收益率不加区分，因此模拟数据没有反映出这一交易偏好差异现象。

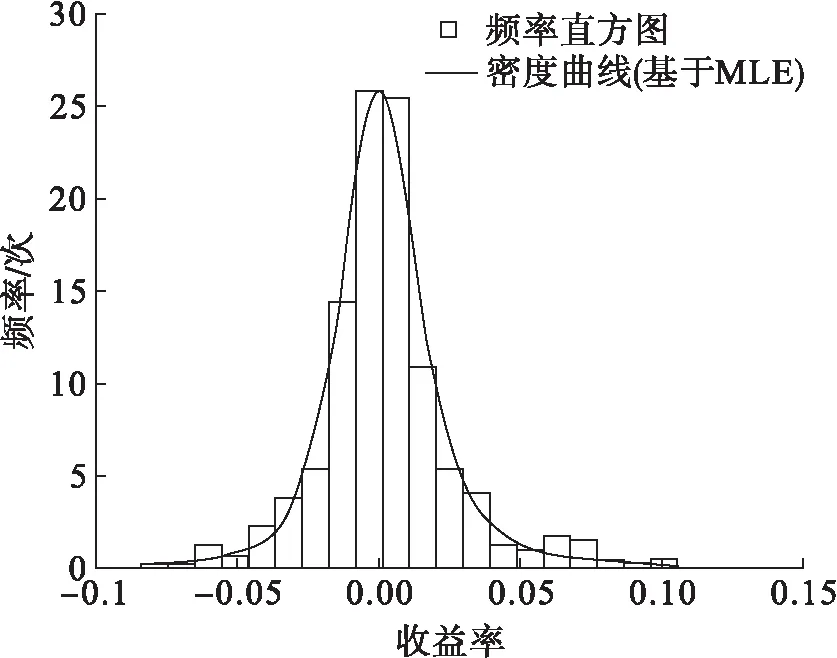
图7 模拟数据频率分布直方图

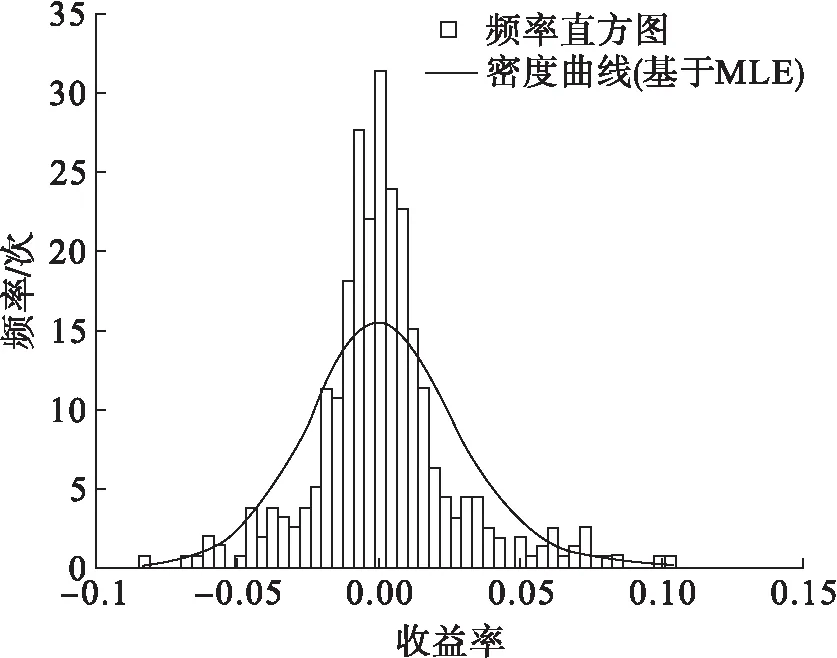
图8 平安银行频率分布直方图

3 结论

通过Sznajd模型的模拟数据所给出的收益率等和实际证券的数据比较，可以看出Sznajd模型所给的价格形成机制和实际证券市场具有一致的统计性质，如都具有相同的尖峰厚尾等普遍特征。与此同时，将Sznajd模型和中国股市的个股比较，我们还能发现个股具有不同的个性特点，如正收益率往往幅度小频率高，负收益往往有一定数量的较大数值，显示出个股收益率上存在着不对称性，通过考虑这种不对称性，可以在金融市场中进一步发展Sznajd模型，使得Sznajd模型的研究更具有应用价值。

参考文献(References)：

[1] MANTEGNA R N,STANLEY H E.An introduction to econophysics-correlations and complexity in finance [M].Cambridge:Cambridge University Press,2000.

[2] PETER E E.Chaos and oder in the capital market [M].New York :John Wiley & Sons,1991.

[3] CHALLER D,MARSILI M,ZHANG Y C.Modeling market mechanism with minority game [J].physica A,2000,276(1):284-315.

[4] WERON K S,WERON R.A simple model of price formation [J].International Journal of Modern Physics C,2002,13(1):115-123.

[5] ISING E.Eeitrag zur therie des ferromagnetismus [J].Z Phys,1925,31(1):253-258.

[6] H OSBORN.Modern theory of critical phenomena[J].Physics Bulletin,1977,28(4):183.

[7] KRAMERS H A,WANNIER G H.Statistics of the two-dimensional ferromagnet.part I[J].Physical Review,1941,60(3):252-262.

[8] 张祥,陈冬保,陈武鸣.二维伊辛模型蒙特卡罗模拟[J].南京大学学报(自然科科学版),1997(1):137-141.

[9] 张志东.伊辛模型的研究进展简介[J].自然杂志,2008,30(2):94-98+101.

[10]郭松青.三维蜂穴Ising模型的磁矩[J].沈阳航空工业学院学报,2000,17(3):54-56.

[11]SILVA L,STAUFFER D.Ising-correlated clusters in the cont-bouchaud stock market model[J].Physica A,2001,294(1):235-238.

[12]涂育松,李晓,邓敏艺,等.一维Sznajd舆论模型相变的研究[J].广西师范大学学报(自然科学版),2005,23(3):5-8.

[13]李其德,王军.基于Ising模型的股票价格统计特征及模拟[J].北京交通大学学报,2007,31(6):81-83.

[14]金华,陆继宗.Ising模型在经济物理学中的应用[J].上海电机学院学报,2008,11(1):66-70.

[15]边宽江,程波,王蕾蕾.收益分布尖峰厚尾问题的统计检验[J].统计与决策,2009(7):83-85.

[16]赵鹏举,刘玉敏.反馈交易与证券市场收益的尖峰厚尾特征[J].系统工程,2009,27(2):7-13.