桥梁结构钢断后伸长率的分布规律与参数

杨帆， 刘兵， 吴元祥， 袁小会， 张红卫， 刘小宁

（武汉软件工程职业学院机械工程学院，武汉430205）

0 引 言

金属材料的断后伸长率是指其试样受外力（拉力）作用断裂时，试样伸长的长度与原来长度的百分比。断后伸长率比较大，表明钢材塑性好，成型加工方便，在生产中不容易出现裂纹；断后伸长率太大，表明钢材强度低，在相同外载时，钢结构显得笨重；如果断后伸长率太小，钢结构在加工中容易出现裂纹，不利于安全生产。因此，断后伸长率是反映钢材塑性的重要指标之一，也是选择钢材型号的依据。

目前，工程上对钢材或者钢结构抗拉强度与屈服强度的分布规律与分布参数进行了一些探索[1-7]，但对钢材断后伸长率的研究并不充分，为给选择钢材型号提供塑性指标的参考依据，文中应用概率论与数理统计知识[8-9]，对钢材断后伸长率分布规律与分布参数的分析方法进行了探索，以桥梁结构钢Q420NHY中厚板室温同质性拉伸试验数据[10-12]为基础，研究了其断后伸长率的分布规律与分布参数。

1 建立分析方法

1.1 同质性试验数据的平均值与精密度

基于概率论与数理统计知识可知，通过有限的有效试验数据，可分析钢材断后伸长率的分布规律与分布参数。为讨论方便，假设钢材断后伸长率A是随机变量。通过拉伸试验测得钢材断后伸长率A的n组同质性试验数据Ai（i=1，2，…，n）时，其断后伸长率的平均值与精密度分别为：

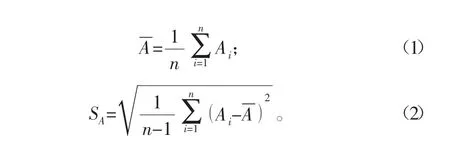
式中分别为断后伸长率平均值与精密度，%。

1.2 分布规律的假设检验

对钢材断后伸长率A分布规律进行假设检验的具体方法是：

1）假设钢材断后伸长率A是基本符合正态分布的随机变量。

2）把n组同质性数据A1、A2、…、An分为M个区间，M=1+3.3lgn，取整数。

3）理论频数。对于符合正态分布的随机变量A，其统计量Ai落在分组区间［a1，a2］，［a2，a3］，…，［aM，aM+1］内的理论概率为：

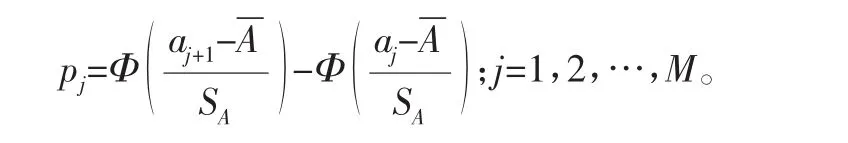
其中：

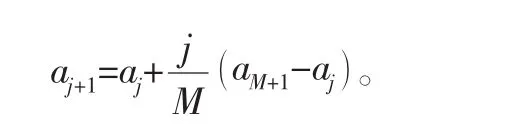
n组同质性数据的统计量Ai位于分组区间［aj，aj+1］内的理论频数为n×pj。

4）计算每个分组区间实际频数Nj与理论频数n×pj差异的皮尔逊统计量之和：

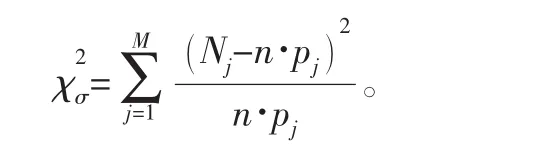
5）确定皮尔逊统计量的临界值对于M个区间，其自由度为f=M-1-2，若取显著度为δ，则由自由度f与显著度δ查得。

6）检验。若则在显著度为δ时，假设成立，否则假设不成立。

工程上一般取显著度δ=0.05[13]，文中所用的χ2分布系数见表1。

表1 χ2系数

1.3 分布参数的取值区间

如果钢材断后伸长率A是基本符合正态分布的随机变量，其分布参数可用均值与标准差表示；均值与标准差的双侧置信度（1-α），是指均值与标准差属于某一区间的概率，其中α是指均值与标准差位于该区间外的概率。文中在双侧置信度（1-α）时，分析均值与标准差的取值区间。在双侧置信度为（1-α）时，断后伸长率均值μA的取值区间为：

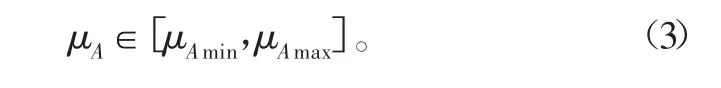
其中

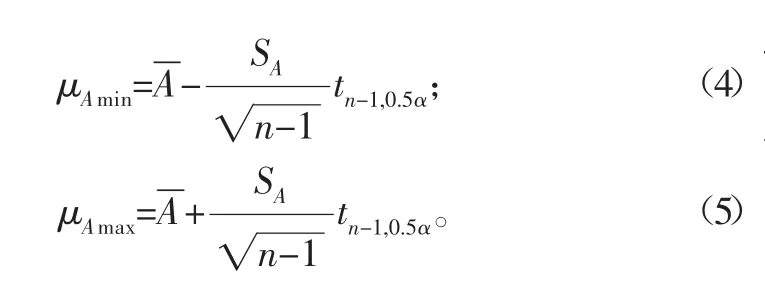
表3 断后伸长率的皮尔逊统计量χ

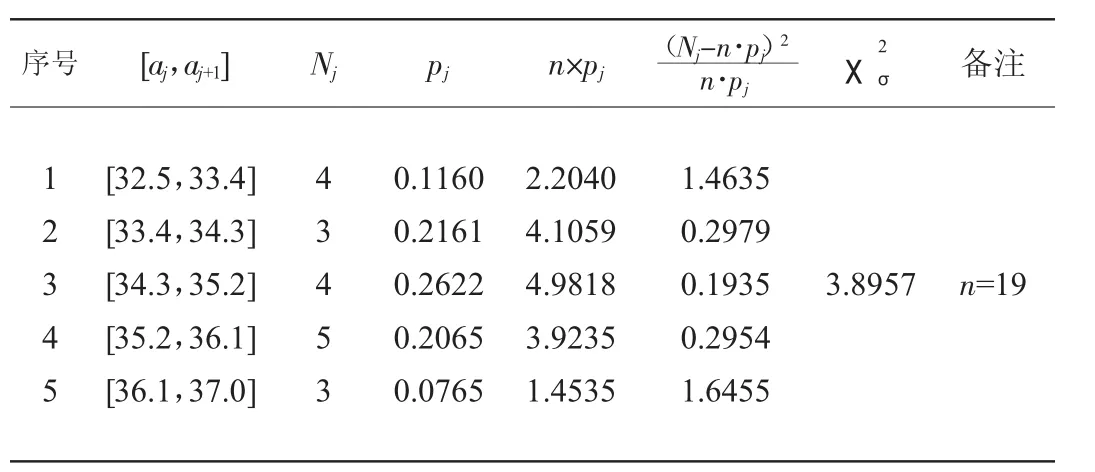
表3 断后伸长率的皮尔逊统计量χ

序号 [aj，aj+1]Nj pj n×pj（Nj-n·pj）2 n·pj χ2 σ备注12345[32.5，33.4][33.4，34.3][34.3，35.2][35.2，36.1][36.1，37.0]43453 0.1160 0.2161 0.2622 0.2065 0.0765 2.2040 4.1059 4.9818 3.9235 1.4535 1.4635 0.2979 0.1935 0.2954 1.6455 3.8957 n=19

式中，μAmin与μAmax分别为断后伸长率均值μA在双侧置信度为（1-α）时的下限与上限，%。

文中取α=0.01，所用t分布系数 t18,0.005取值 2.878。在双侧置信度为（1-α）时，断后伸长率标准差σA的取值区间为

其中：

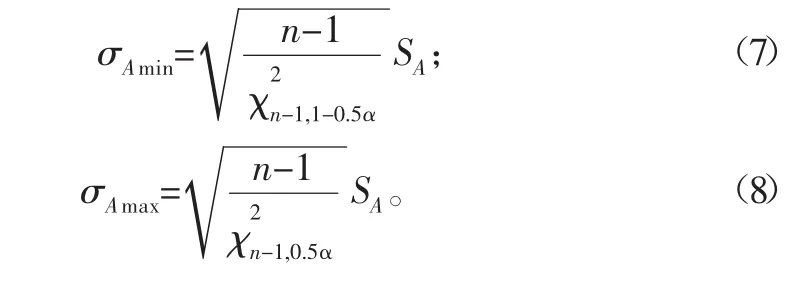
式中，σAmin与σAmax分别为断后伸长率标准差在双侧置信度为（1-α）时的下限与上限，%。

工程上一般取α=0.01，文中所用χ2分布分布系数见表1。

2 同质性试验数据及统计

Q420NHY是桥梁结构钢[14]，文献［10］按标准[15]制作标距为50 mm试样，在UHF500KNI型液伺服万能试验机上，获得了Q420NHY室温断后伸长率的20组试验数据；在数据同质性的双侧置信度为98%时，文献［11］分析认为其中19组试验数据具有同质性，现将同质性断后伸长率试验值由小至大排列见表2，相应的统计数据也列入表2。

表2 19组同质性试验数据统计

3 断后伸长率的分布规律与分布参数

3.1 分布规律

假设Q420NHY钢室温断后伸长率基本符合正态分布。根据断后伸长率的同质性试验数据，将其分别分为5个区间，自由度f=5-1-2=2，取显著度δ=0.05，由表1可知，皮尔逊统计量的临界值χ22,0.05=5.991。

在Q420NHY钢断后伸长率的每个分组区间，实际频数Nj与理论频数n×pj差异的皮尔逊统计量之和见表3。

由表3可知：断后伸长率的皮尔逊统计量之和χ2σ为3.8957，小于临界值5.991，表明显著度为0.05时，Q420NHY钢室温断后伸长率是基本符合正态分布的随机变量。

3.2 分布参数

在双侧置信度为99%时，将表2的断后伸长率有效统计值代入式（3）~式（8），得到Q420NHY钢室温断后伸长率均值μA和标准差σA的取值区间：

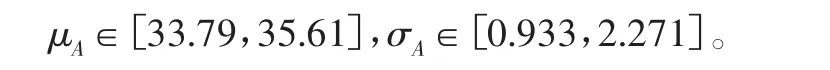
4 结语

1）在试验数据同质性的双侧置信度为98%时，基于拉伸试验数据，应用概率论与数理统计知识，建立了研究Q420NHY钢室温断后伸长率分布规律与分布参数的方法。

2）显著度为0.05时，Q420NHY钢室温断后伸长率是基本符合正态分布的随机变量。

3）双侧置信度为99%时，Q420NHY钢室温断后伸长率的均值不小于33.79%且不大于35.61%，标准差不小于0.933%且不大于2.271%。

[1]刘岑,吴元祥,刘兵,等.奥氏体不锈钢S30408抗拉强度分布规律研究[J].河北工业科技,2016,33(1):31-34.

[2]郑津洋,王珂,黄泽,等.液氮温度下奥氏体不锈钢强度试验研究[J].压力容器,2014,31(8):1-6.

[3]李清,袁小会,刘岑,等.有效试验数据对钢材机械性能分布规律的影响[J].武汉工程大学学报,2015,37(4):69-73.

[4]黄泽,缪存坚,李涛,等.预拉伸奥氏体不锈钢常温拉伸力学性能试验研究[J].压力容器,2013,30(6):7-11.

[5]刘小宁,刘岑,张红卫,等.单层与多层球形容器爆破压力的概率分布[J].武汉工程大学学报,2015,37(7):49-54.

[6]刘岑,袁小会,刘兵,等.钢制单层球形容器爆破压力的计算[J].武汉工程大学学报,2016,38(3):299-306.

[7]杨帆,刘岑,刘兵,等.钢制薄壁容器爆破压力计算公式评价[J].现代制造工程,2016(11):124-128.

[8]熊德之,张志军.概率论与数理统计及其应用[M].北京:科学出版社,2007:131-262.

[9]化学工程手册编辑委员会.化工应用数学[M].北京:化学工业出版社,1983:23-28,369-375.

[10]薛欢.桥梁结构钢拉伸试验不确定度的评定[J].武汉工程职业技术学院学报,2017,29(1):11-14.

[11]刘岑,杨帆,吴元祥,等.钢材拉伸试验数据同质性的判别[J].武汉工程职业技术学院学报,2017,29(2):17-19.

[12]杨帆,刘岑,叶志娟,等.U肋内焊技术的工艺参数优化研究[J].武汉工程职业技术学院学报,2017,29(1):15-17.

[13]徐灏.机械强度的可靠性设计[M].北京:机械工业出版社,1984:1-220.

[14]桥梁用结构钢:GB/T714-2015[S].

[15]金属材料拉伸试验第1部分:室温试验方法:GB/T228.1-2010[S].（责任编辑 马忠臣）