最优时间的无零矢量有限状态预测控制
张海玮, 吴爱国
(1. 天津大学 电气自动化与信息工程学院,天津 300072;2. 天津大学 仁爱学院,天津 301636)
随着国民经济的迅速发展和环境需求的日益加剧,太阳能、风力、潮汐发电等新型可再生清洁能源得到全面发展.把可再生能源产生的电能转换至电网或负载,三相逆变器作为核心环节,其控制性能直接影响入网电能质量或用电负载的工作性能.目前,三相逆变器的控制策略主要包括电压控制和电流控制.其中电流预测控制以开关状态建立模型,属典型非线性控制策略.而有限状态预测控制方式在单环内实现多变量控制,具有较快的动态响应特性.在功率变换器有限控制集模型预测控制中,系统预测模型直接根据变换器被控电流量与开关函数组合的关系构建,充分利用电力电子变换器的离散化特点,即不对开关动作的瞬间建模,而是对开关动作的结构建模.而在每个采样周期内构建的模型为线性,开关函数组合状态不变.预测控制策略与正弦脉宽调制(Sinusoidal Pulse Width Modulation,SPWM)控制相比,无须脉冲宽度调制(Pulse Width Modulation,PWM)模块,更容易数字化实现.
很多电路拓扑结构均可采用有限控制集模型预测控制策略,如广泛应用的三相逆变器[1-4]、多电平逆变器[5-7]和矩阵变换器[8-9].文献[10]主要针对同步发电机的参考电压优化选择,用估计定子电流代替测量电流实现了较低的电流总谐波失真.文献[11-12]通过构建价值函数控制负载电流,使共模电压保持在较低值.文献[13]为减小计算量,在两步内应用相同的开关函数组合,降低了开关频率,同时减少了开关损耗.有限控制集模型预测控制拓朴结构不同,产生的开关函数组合数量也不同,如三相二电平逆变器的开关状态为 23= 8,三相三电平的开关状态为 33= 27.在开关周期内实时计算每个开关函数组合,计算量较大.与常规拓扑结构相比,多电平电路计算量会更大.在电力电子变换电路中,二电平电路在开关周期内对开关组合状态的计算量相对较少.
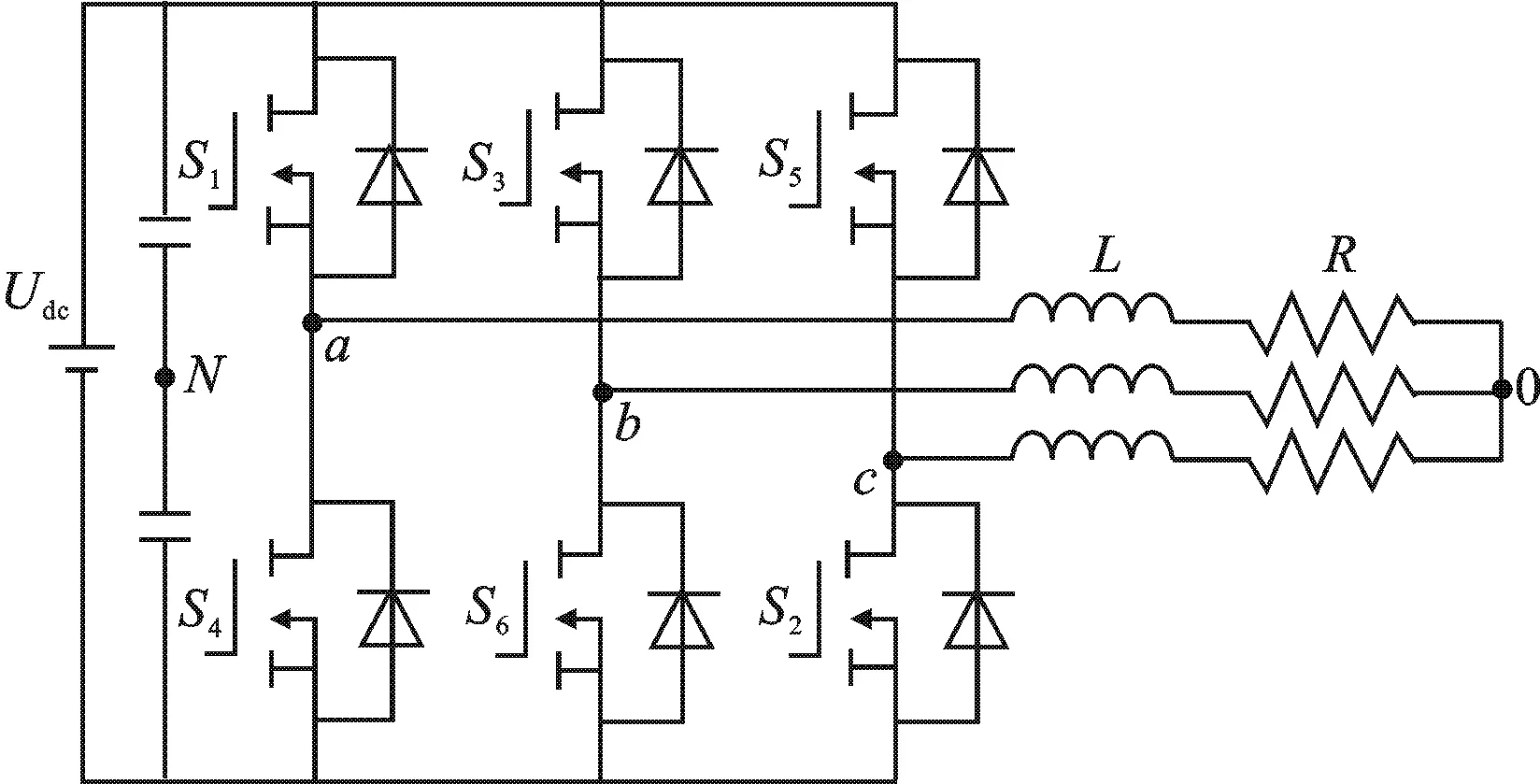
图1 三相电压型逆变器
针对三相逆变二电平电路运行特性和交流侧共模电压抑制需求,笔者提出基于最优时间序列的有限控制集模型预测控制.为了抑制逆变器交流侧共模电压,在传统有限控制集预测控制中去除零矢量,构建基于α,β轴电流误差代价函数.以代价函数最小为原则,计算每个非零矢量作用的最优时间,最终得到最优作用时间的非零矢量序列.
1 三相逆变器的数学模型
1.1 三相电压型逆变器
如图1所示,三相电压型逆变器拓扑结构由直流电源Udc、功率器件、滤波电感L和负载电阻R组成.S1~S6均为功率器件,每一相功率变换器的开关状态如下:
三相电压型逆变器交流输出侧共模电压Ucm为
(1)
逆变器交流输出侧共模电压与每相上、下桥臂功率变换器的开关状态有关.三相逆变器包括3组桥臂,可产生8组不同的开关组合(如表1所示),共产生4种共模电压值.当功率器件状态不同组合时,三相电压型逆变器交流输出侧共模电压有4种数值.当状态组合为零矢量(0状态和7状态)时,交流输出侧共模电压绝对值达到最大值(为Udc/2).而其余6种非零矢量所产生的共模电压绝对值为Udc/6,仅为共模电压峰值的 1/3.由此可知,不应用零矢量可大幅度减小电压型逆变器交流输出侧的共模电压.

表1 不同开关状态组合下的共模电压
1.2 三相逆变器的预测数学模型
结合上节的分析,若只取6种非零矢量,可得到6种不同电压矢量.由图1所示电路变量定义,逆变器在静止α,β坐标下输出电流动态矢量模型为
(2)
其中,R为输出负载,L为滤波电感,iα、iβ、uα和uβ分别表示电流、电压在α、β轴的分量.
实现有限控制集模型预测控制的第1步是对拓扑结构进行建模,且所构建模型与实际系统的一致性决定了控制性能的优劣.而实际上,在任一时刻及任一建模精度均存在建模误差,所以从tk时刻评估tk+1时刻的预测组合状态时,用tk时刻的电路采样电流,以减小误差:
(3)
其中,TS为系统采样时间,负载电流导数近似于前向欧拉逼近.
在第k时刻,分别对三相逆变器作用6组非零矢量u(k),预测第k+1时刻三相逆变器负载电流的输出值.预测第k+1 时刻负载电流为
(4)
其中,下标p表示此值为预测值.
2 无零矢量有限状态预测控制方法
为了减小三相逆变器输出侧共模电压,应避免使用零矢量.去除零矢量后,与传统有限控制集(Finite Control Set,FCS)预测控制相比,开关状态矢量只有6种.在执行此算法的过程中,在每采样周期内选择最优非零矢量实施控制.
在理想情况下,忽略所需计算时间,在第k时刻测得电流并计算出各个开关状态组合,选择在第k+1 时刻使得价值函数最小化的开关状态,并即刻应用于第k时刻,则第k+1 时刻实时采样到的负载电流输出值应与预测值一致.但由于采样率和微处理器计算速度的限制,测得负载电流输出值的第k时刻与所选开关状态应用的第k+Tp(Tk 式(6)中,iα-p,iβ-p是非零电压矢量作用下第k+2时刻的预测电流ip的实部和虚部;iα-ref,iβ-ref是第k+2 时刻的理想电流iref的实部和虚部. 在每个计算周期内,有限状态预测控制方法通过分别计算每个开关状态的价值函数,选取其中价值函数最小的电压矢量状态作为下一时刻的开关组合状态.通过评估第k+2 时刻的负载电流预测值,可有效弥补控制器计算延时带来的误差,且未明显增加控制器的计算量. 去除了零矢量之后,三相逆变器输出侧共模电压得到明显抑制.然而,由于缺少保持原状态的零矢量,导致逆变器负载电流输出值更多地偏离参考值,使波形质量下降,谐波失真增加.为此,有必要考虑一种优化控制算法,在舍弃零矢量的情况下,仍能保持较优的波形输出. 电流预测的目标是使实际输出电流值和参考电流值之间误差最小.为了最大程度地实现控制目标,采用最小二乘算法构造价值函数,如式(6). 针对价值函数式(6),对每个非零矢量分别计算开关周期内的最优作用时间,由此选出最优非零矢量及其优化作用时间: ∂g∂ts=0 .(7) 由式(6)和式(7),可得 (8) 通过式(8)可计算出最优控制时间,在最优时间基础上使得价值函数g最小.由式(8)可看出,各组非零矢量的最优时间不同.当选用某一开关组合状态后,意味着最优时间也被确定下来,并将该优化时间作为此开关组合状态的作用时间,达到最优的控制效果.采用最优时间预测控制方式使得每个采样时间不固定,并造成电力电子器件通断频率增高.为保证功率器件正常工作,不超过其限制频率,设置最优时间的上下限:tmin≤ts≤tmax.其中tmin为功率器件最小开关时间,tmax为满足电流输出谐波的采样最大时间.三相逆变器有限控制集预测控制每步平均实时计算时间大约为 3.5× 10-6s,瞬时计算时间为 3.15× 10-6s. 图2 有限状态预测控制(去除零矢量)图3 去除零矢量的时间最优有限状态集预测控制 图4 三相逆变器交流侧共模电压(去除零矢量) 三相逆变器平台核心控制器是FGPAepc2c12q240,母线电压为 250 V,R=10 Ω,L=10 mH.图2所示为已去除零矢量有限状态预测控制的电流响应.抑制共模电压去除零矢量后,负载电流谐波略有增加,且输出三相波形不对称性也增强.图3中采用时间最优序列来提高预测控制器的输出性能,减小负载电流的谐波.图3中负载电流总谐波失真(THD)为2.97%,明显低于图2所示的电流谐波失真(5.43%).改进控制方式能较好地实现参考电流跟踪,减小三相输出电流总谐波失真.两种方式的采样频率一致,但应用时间最优有限控制集模型预测控制时平均开关频率有所提高.图4所示三相逆变器交流侧Ucm为 1/6 直流母线电压,减小至 ±41.6 V.结合1.1节的分析,表明去除了绝对值最大值为 1/2 直流母线电压的交流输出侧共模电压. 为大幅度降低三相逆变器交流侧共模电压Ucm,在传统有限控制集预测控制基础上去除零矢量,但输出电流出现较大纹波,且不对称性增加.为解决此问题,笔者提出基于时间最优的有限控制集模型预测控制,并详细阐述了设计过程.计算每组非零矢量的最优时间,在α,β轴电流误差代价函数误差最小的前提下,确定非零矢量的开关组合.实验表明,基于时间最优的有限控制集模型预测控制可有效地降低共模电压,抑制三相输出电流谐波失真,弥补了稳态控制精度,但开关频率有所增加. [1] LEE S S, HENG Y E. Current Controller of Three-phase VSI Using FCS-MPC with Optimal Active and Zero Vector Selection for Balanced Loss Distribution and Switching Loss Reduction[J]. International Transactions on Electrical Energy Systems, 2017, 27(2): e2250. [2] HASSINE I M B, NAOUAR M W, MRABET-BELLAAJ N. Model Predictive-sliding Mode Control for Three-phase Grid-connected Converters[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1341-1349. [3] ROHTEN J A, ESPINOZA J R, MUNOZ J A, et al. Model Predictive Control for Power Converters in a Distorted Three-phase Power Supply[J]. IEEE Transactions on Industrial Electronics, 2016, 63(9): 5838-5848. [4] BAYHAN S, TRABELSI M, ABU-RUB H. Model Predictive Control of Three-phase Three-level Neutral-point-clamped qZS Inverter[C]//Proceedings of the 2016 10th International Conference on Compatibility, Power Electronics and Power Engineering. Piscataway: IEEE, 2016: 410-415. [5] TRABELSI M, BEN-BRAHIM L, GASTLI A, et al. An Improved Predictive Control Approach for Multilevel Inverters[C]//Proceedings of the 2013 IEEE International Symposium on Sensorless Control for Electrical Drives and Predictive Control of Electrical Drives and Power Electronics. Piscataway: IEEE, 2013: 6684486. [6] RIAR B S, GEYER T, MADAWALA U K. Model Predictive Direct Current Control of Modular Multi-level Converters[C]//Proceedings of the 2013 IEEE International Conference on Industrial Technology. Piscataway: IEEE, 2013: 582-587. [7] VATANI M, HOVD M. Predictive Control of Converter Switches in a Multi-terminal HVDC System[C]//Proceedings of the 2013 39th Annual Conference of the IEEE Industrial Electronics Society. Piscataway: IEEE, 2013: 3699-3704. [8] NADEMI H, NORUM L E, SOGHOMONIAN Z, et al. Low Frequency Operation of Modular Multilevel Matrix Converter Using Optimization-oriented Predictive Control Scheme[C]//Proceedings of the 2016 17th IEEE Workshop on Control and Modeling for Power Electronics. Piscataway: IEEE, 2016: 7556709. [9] RIVERA M, RODRIGUEZ J, GARCIA C, et al. A Simple Predictive Voltage Control Method with Unity Displacement Power Factor for Four-leg Indirect Matrix Converters[C]//Proceedings of the 2012 15th International Power Electronics and Motion Control Conference and Exposition. Piscataway: IEEE, 2012: DS2c. 51-DS2c. 56. [10] ABDELRAHEM M, HACKL C M, KENNEL R. Simplified Model Predictive Current Controlwithout Mechanical Sensors for Variable-speed Wind Energy Conversion Systems[J]. Electrical Engineering, 2017, 99(1): 367-377. [11] GONG Z, DAI P, WU X, et al. A Hierarchical Model Predictive Voltage Control for NPC/H-bridge Converters with a Reduced Computational Burden[J]. Journal of Power Electronics, 2017, 17(1): 136-148. [12] WANG G F, JIANG J G, WU W. Nonlinear FCS-MPC Strategy of NPC/H-5L Inverter Based on Satisfactory Optimization Algorithm[J]. Chaos Solitons & Fractals, 2016, 89:353-362. [13] CORTES P, RODRIGUEZ J, VAZQUEZ S, et al. Predictive Control of a Three-phase UPS Inverter Using Two Steps Prediction Horizon[C]//Proceedings of the 2010 IEEE International Conference on Industrial Technology. Piscataway: IEEE. 2010: 1283-1288.3 基于最优作用时间的无零矢量有限状态预测控制
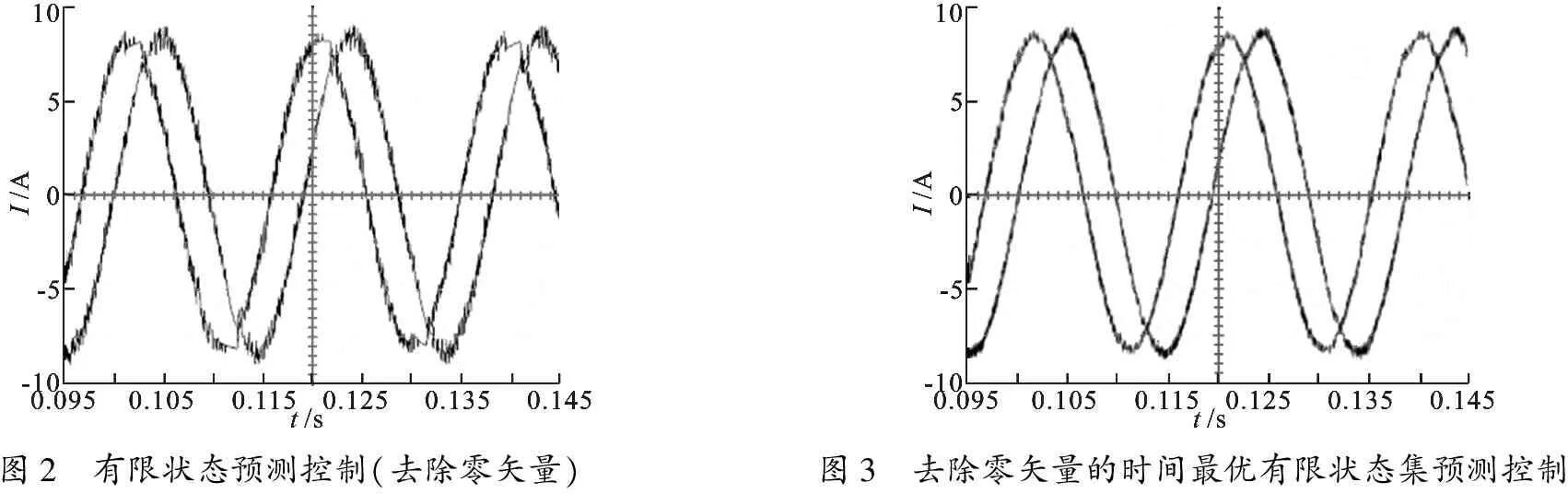
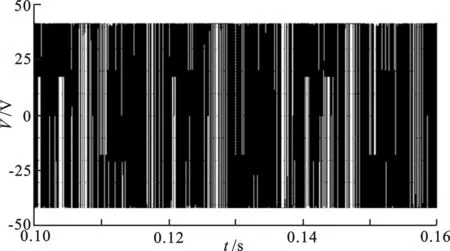
4 实验分析
5 总 结

