数学建模中的数据处理
范馨香
(福建师范大学协和学院,福建福州 350108)
作为发现人才的有效手段之一,数学竞赛活动倍受世界发达国家的重视。一些重大数学竞赛的优胜者,大多在他们后来的事业中卓有建树,例如“国际领袖数学家之一”华罗庚,“中国航天之父”钱学森,“微分几何之父”陈省身先生等.而作为一种数学教育活动的数学建模竞赛(CUMCM),对于推进大学数学教学改革有着重大意义,影响深远。自1992年我国开办这一竞赛活动以来,数学建模竞赛卓有成效地促进了数学教学改革,成为培养应用型创新型人才的重要环节。清华大学数学系谢金星教授言简意赅地描绘数学建模如下:数学建模是数学与实际问题的桥梁:首先,利用“归纳”将现实对象的信息表述为数学模型;接着,用“演绎”求解得到数学模型的解答并解释为现实对象的解答,最后验证模型是否符合现实对象的信息。在“归纳”、“演绎”即表述模型和求解的过程中,往往需要较大的计算量,包括数据处理,数值计算等等,这些都要用计算机和数学软件求解过渡,以达到事半功倍的效果。本文以2010年全国大学生数学建模竞赛B题为例,谈谈常用的数据处理软件(Excel、SPSS、Matlab)在数学建模中的应用。
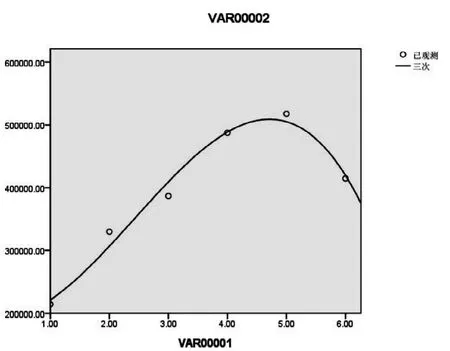
图1 04-09年1月入境旅客量趋势图
1 问题的提出
2010年全国大学生数学建模竞赛B题是“上海世博会影响力的定量评估”,原题目省略。
上海世博会是中国举办的一盛大活动,本届世博会将对上海的旅游效益产生巨大影响。旅游的效益与旅客流量和旅游收入密切相关。本文侧重评估世博会对上海入境旅游人数的影响力。建立入境旅游人数的有效预测模型,通过比较2010年1月至7月入境旅游人数的预测值与实际值,评定出世博会对旅游人数的影响力。
2 数据的搜集、分析
每一年上海的入境旅游人数受季节因素,假期因素等影响而变化。如5月和10月都有黄金周,必然促进旅游人数的增长,借助统计年鉴收集2004到2009年各月份的具体数据。旨在分析各年同一个月份的入境旅游总人数的数据,减少干扰因素。用Excel软件整合统计数据(单位:人)表格,其中第一行为年份,第一列为月份。
以年份为自变量,以各月份入境人数为因变量,输入SPSS软件中进行曲线估计。回归的曲线估计模型分别采用线性、二次项、复合、增长、对数、立方、S(S)、指数分布、逆模型、幂、logistic这些模型来拟合曲线。例如,作出1月份入境旅游人数的拟合曲线。拟合后,以R方为判断指标,比较各种模型的R方值,R方的值越大,曲线的拟合效果越好。比较得到三次方程的R方等于0.979值最大。因此,采用立方模型作为1月份入境人数的曲线估计模型。
用同样的方法,相继确定出2月到12月份的入境旅游人数拟合曲线,均是立方模型的效果最佳。
3 模型的建立、检验
根据已确定的立方模型,具体解析求出各月份的拟合曲线。如图1呈现的是2004年到2009年1月份入境旅客流量走势图。
根据04-09年1月份的模型汇总和参数估计值可以得出1月份的入境人数的预测模型:
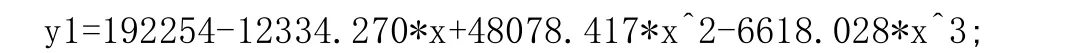
用同样方法(具体模型参数略)相继得出其他各月份的预测模型:
y2=286658.667-72594.827*x+60786.742*x^2-7289.574*x^3;
y3=133408.667+229454.280*x-32148.437*x^2+748.426*x^3;
y4=98421.333+284161.335*x-55469.587*x^2+3457.935*x^3;
y5=83133.333+253850.239*x-37208.194*x^2+1043.852*x^3;
y6=40620.000+347070.865*x-78194.024*x^2+5397.111*x^3;
y7=84640.667+300217.634*x-68139.067*x^2+5121.870*x^3;
y8=11858.333+421759.87* x-110390.837*x^2+9183.435*x^3;
y9=113257+299732.087* x-69718.940*x^2+5195.972*x^3;
y10=83084.667+374465.193*x-80947.853*x^2+5566.954*x^3;
y11=131083+302096.893*x-67794.929*x^2+5265.75*x^3;
y12=158375.333+258504.541*x-68167.528*x^2+5704.074*x^3;
根据以上的方程,利用Matlab软件分别计算出04至09年的各个月份预测的入境人数总值(单位:人),结果可列表,第一行为年份,第一列为月份。
将预测的值与实际的值相比较,计算两者的比值,比值越接近1越精确,据此,用Excel软件求得模型的平均比值:
1月份比值为1.001813 2月份比值为1.007375 3月份比值为1.002784
4月份比值为1.000914 5月份比值为1.001033 6月份比值为1.00297
7月份比值为1.000332 8月份比值为1.000934 9月份比值为1.000272
10月份比值为1.00048 11月份比值为1.000139 12月份比值为1.003516
因此模型整体的平均比值为1.00188,模型预测的相似度高。
误差率=|1-比值|*100%,对各年各月的误差率进行求和,并取平均值,得出模型的平均误差率:
1月份误差率为0.181%;2月份误差率为0.738%;3月份误差率为0.278%;
4月份误差率为0.091%;5月份误差率为0.103%;6月份误差率为0.297%;
7月份误差率为0.033%;8月份误差率为0.093%;9月份误差率为0.027%;
10月份误差率为0.048%;11月份误差率为0.014%;12月份误差率为0.352%;
因此模型整体的平均误差值为0.188%,模型预测的可信度高。
4 模型的应用、解答
根据已经求出的预测模型,预测2010年的上海入境旅游人数.预测结果与实际数据进行相互印证:实际入境人数与预测人数及增长率各月份的数据可以表格形式呈现“实际与预测的对比”,例如,第一列为月份,第二列为实际入境人数,第三列为预测人数,第四列为增长率。
首先,可以得出在世博会的影响下,各个月份的入境旅游人数普遍增长,增长率为:
2010年1月份增长率为1.821187;2010年2月份增长率为0.866656;
2010年3月份增长率为0.649222;2010年4月份增长率为0.219535;
2010年5月份增长率为0.807199;2010年6月份增长率为0.544649;
2010年7月份增长率为0.2403。
对以上增长率求平均值,得出平均增长率为:73.55%。
应用模型对搜集到的数据进行定量评估,可以判断出在世博会的影响下,上海的入境旅游人数平均增长73.55%。
其次,经过对搜集的上海2000年至2009年的旅行各项数据进行统计,数据中有四项指标:入境旅游人数、国内旅游人数、外汇收入、国内旅游收入。设定旅游收入为判断旅游效益的主要指标,可以求出入境旅游人数对整体旅游效益的影响程度,整理2000-2009旅游概况结果如下:入境旅游总人数(AT)为 5934.65万次,国内旅游总人数(DT)为112067.58万次,外汇总收入(AI)为3374.000855亿元,国内旅游总收入(DI)为15932.22573亿元,由以上数据计算入境旅游的比重=(AI/AT)÷(AI/AT+DI/DT),求得入境旅游占总旅游比重为0.803457161。入境旅游占总旅游效益的比重较大,在世博会的影响下,入境人数明显增加,入境旅游收入必然也随之增长。
5 结语
本例可以充分显示SPSS、Matlab处理数据的强大功能,另外还有Mathematica,它的大小适中,了解使用的人也很多,国内能找到的参考资料也比较多;而在处理线性、非线性规划等问题时,采用SAS,Lingo等软件会比较方便,总之,数学软件是数学建模的必不可少的重要工具,在数学建模的教学和赛前培训中,适当介绍数学实验中的一些软件,会有比较理想的效果[1]。
[1]李大潜.将数学建模思想融入数学系主干课程[J].中国大学数学,2006,(1):9-11.

