经管类本科毕业论文成绩评定方法探讨——基于学业平均成绩与毕业论文成绩的分布拟合检验

屈国强（河南理工大学 财经学院，河南 焦作 454000）

0 引 言

本科毕业论文撰写是经管类人才培养方案中一个重要的综合性实践教学环节，要求学生综合运用所学专业知识和基本技能来独立分析和解决科研、生产和社会实践问题。它是对学生科学思维、实验研究、技术分析、学术规范等能力的全面检验，直接反映了学生专业综合素质以及对专业理论和技术的掌握程度。同时，本科毕业论文质量在一定程度上也反映了高校管理水平、教师教研层次和学生培养质量。而本科毕业论文成绩评定是一个重要评价手段，其结果也是对学生4年学习成效的一个综合衡量。

目前，对于本科毕业论文成绩的评定方法存在较多争议。文献[1]对于应用化学专业本科毕业论文成绩评定过程与方法进行了详细介绍。文献[2]建立了包括4个一级指标和18个二级指标的本科毕业论文评价体系，采用综合加权评价法进行评价。文献[3]认为受诸多因素的影响，用传统的加权平均法对学生毕业论文质量进行评价很难保证客观公正。建立了包括4个一级指标和12个二级指标的本科毕业论文评价体系，利用BP神经网络法建立综合评价模型进行评价。文献[4]指出单一质量评价体系不能反映学生真实水平，借助层次分析法计算评价指标权重后采用传统加权平均法与模糊综合评价法计算学生毕业论文成绩。文献[5]构建了理工科毕业论文质量评价体系结构，采用层次分析法进行分析评价。文献[6]采用熵权模糊综合评价模型以求客观准确评价本科生毕业论文质量。

关于学生学业成绩总体分布情况，文献[7]指出学生总体学习成绩分布有正态分布、正偏态分布、负偏态分布、双峰型分布、平坡型分布。文献[8]认为凡符合教学规律的考试，其总成绩应服从或接近服从正态分布，当考题质量偏离教学目的时，总体成绩还会经常出现偏态分布。文献[9]指出按照经典的教育测量学，考试成绩的分布应该是正态分布。文献[10]指出由于测验的目的、真实难度、测验样本的同质性或异质性、样本大小等因素的影响，学生成绩测验分数正态分布不可能完全做到。文献[11]用某学院第一学期所有课程成绩进行正态性检验和描述性分析，结果表明学期成绩呈负偏态分布，这与成绩的结构、教师的授课效果和试题的难易程度有关。文献[12]对于延安大学某专业高等代数成绩进行分析，表明高等代数1的成绩服从正态分布，而高等代数2和解析几何的成绩不服从正态分布。文献[13]研究表明某职业大学绝大多数课程总评成绩符合正态分布。文献[14]通过对影响学生学业成绩分布因素的分析，认为追求学生学业成绩呈正态分布存在弊端，应辩证地看待学生学业成绩分布，偏态分布也具有合理性。此外，文献[15]研究表明平时成绩与学习总成绩呈现极其显著的正相关。

在上述研究基础上，本文采用χ2拟合检验的方法，检验经管类本科学生学业平均成绩与毕业论文成绩的分布是否一致，结果表明传统毕业论文成绩综合评价方法确实存在缺陷，不能反映学生4年学业的真实成绩，因而需要改进。

1 毕业论文成绩评定方法

河南理工大学财经学院学生毕业论文成绩评定基本沿用传统的综合评价方法，分5步进行。

（1）指导教师评分。指导教师根据学生毕业论文写作过程的综合表现，结合论文选题难易程度、写作态度、论文质量、创新程度等，确定指导教师评分。

（2）评阅教师评分。由职称较高的教师担任评阅教师，根据自己的经验判断，以及论文选题、写作质量、创新程度等，确定评阅教师评分。

（3）答辩小组评分。答辩小组每一位教师根据学生论文选题、写作质量、创新程度、答辩表现、论文知悉程度等打出分数，经过简单平均计算，确定答辩小组评分。

（4）确定毕业论文总成绩。指导教师评分、评阅教师评分、答辩小组评分的权重分别为30%、30%和40%，经加权平均计算，确定毕业论文总成绩。

（5）进行等级划分。根据毕业论文总成绩落入的分值区间，以优、良、中、及格和不及格进行等级划分。

虽然这种方法程序正确，但主观性较强，系主任、教授等评分的影响力较大，不可避免会出现人情分，学生的感受与得分存在较大的差距，导致学生与老师对最终学生毕业成绩等级划分颇有微词，但又提不出有说服力的理由。

一般认为一个学生如果学习非常努力，表现在学业平均成绩分数较高，那么作为衡量学生4年综合学业成绩的毕业论文成绩也应该是较好的；反之，其毕业论文成绩也不会较好。为确定现行毕业论文成绩综合评定方法是否科学合理，能否反映学生的真实学业成绩，检验学生学业平均成绩与其毕业论文成绩的概率分布是否拟合。若拟合，说明现行毕业论文成绩评定方法是合理的，否则不合理。

2 学业平均成绩与毕业论文成绩概率分布的一致性检验

概率论与数理统计中的中心极限定理指出，在客观实际中有许多随机变量，它们是有大量的相互独立的随机因素的综合影响所形成的，而其中每一个个别因素在总的影响中所起的作用都是微小的。这种随机变量往往近似地服从正态分布[16]。因此，可以推断学生学业平均成绩近似地服从正态分布。同理，也可以推断学生毕业论文成绩也近似地服从正态分布。

选取河南理工大学财经学院国贸03-1班和03-2班学生学业平均成绩和毕业论文成绩作为样本进行检验。国贸03-1班和03-2班分别有31人、34人，其学业平均成绩如表1、表2所示，其学业平均成绩分布、毕业论文成绩分布如表3、表4所示。按惯例，成绩值在90～100之间评定为优秀等级，80～89之间为良好，70～79之间为中等，60～69之间为及格，60以下为不及格。

表1 国贸03-1班学生学业平均成绩

一般认为学生毕业论文的成绩应高度映射其在大学4年学业平均成绩，学生学业平均成绩的概率分布与毕业论文的成绩的概率分布应该是一致的。但是，事实的确如此吗？本文做出检验：

H0：学生学业平均成绩的概率分布与其毕业论文成绩的概率分布是一致的。

本文采用χ2拟合检验法[16]，选用作为检验统计量。

其中，k表示学生学业平均成绩或毕业论文成绩的等级数，i表示成绩等级（i=1,2,…,k），n表示样本容量，pi表示事件Ai（Ai表示成绩等级i这一事件） 发生的概率pi=p（Ai），fi表示样本观察值落在事件Ai的个数。取显著性水平α=0.05。

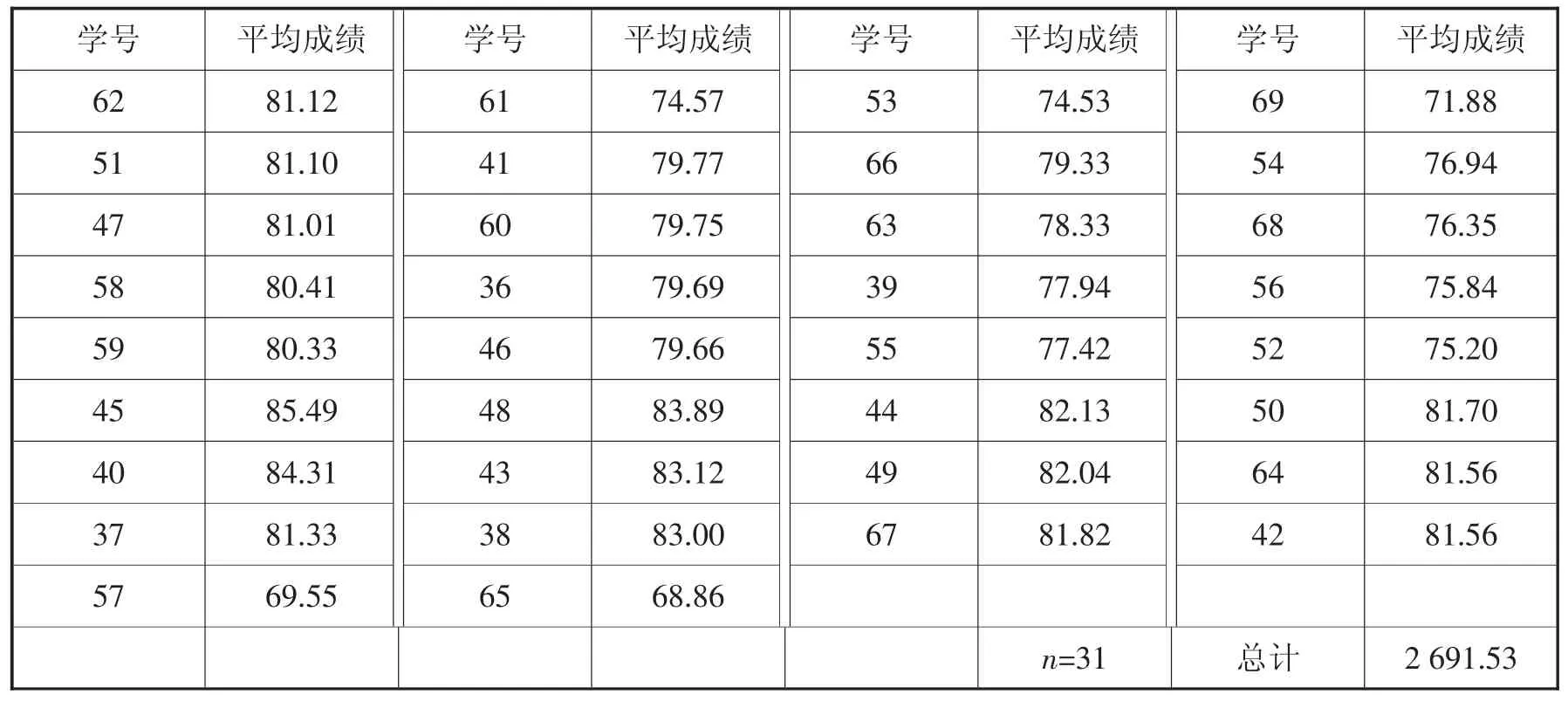
表2 国贸03-2班学生学业平均成绩

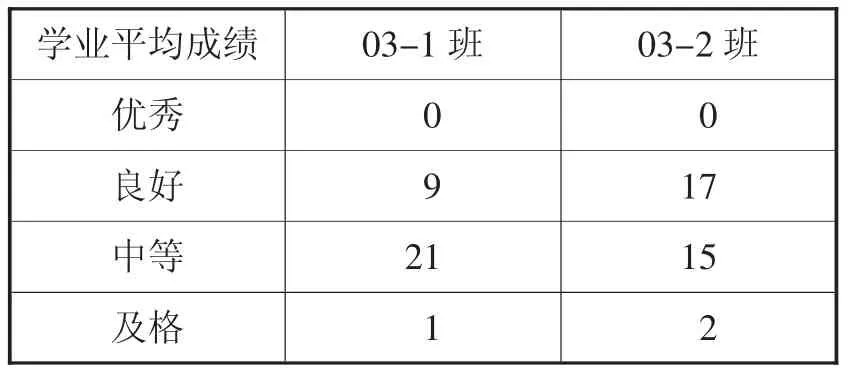
表3 国贸03-1、03-2班学业平均成绩分布表（人数）

表4 国贸03-1、03-2班毕业论文成绩分布表（人数）

由皮尔逊定理[16]可知，若样本容量n充分大（大于50即可）则当H0为真时，上述统计量近似地服从χ2（k-1）分布，且按上述统计量计算出来的χ2不应太大。如χ2过大，就拒绝H0，因而拒绝域的形式为：χ2≥G（G为正常数）。

由上述定理知G=χ2（k-r- 1）（r为被估计的参数的个数，在本文中，r=0），于是拒绝域为：

即当样本观察值使的χ2值有时，则在显著性水平α下拒绝原假设H0，否则就接受H0。根据实践，要求样本容量不小于50，以及每个npi都不小于5，否则应适当地合并事件Ai，以满足这个要求。采用上述数据，列出χ2拟合检验计算表，如表5所示。

表5 χ2拟合检验计算表

经计算知 χ2=75.83-65=10.83，k=4，r=0, 查 χ2分布表[16]，可得：

故拒绝H0，认为学生学业平均成绩概率分布与其毕业论文成绩概率分布的差异是显著的。就是说，现行毕业论文成绩评定方法的有效性是值得怀疑的。

3 学业平均成绩与毕业论文成绩的均值与方差

用最大似然估计法[16]计算学生学业平均成绩均值μ与方差σ2的最大似然估计量为：

由于样本方差是总体方差σ2的无偏估计，所以用样本方差作为总体方差 σ2的估计值。

同样选取国贸03-1班和03-2班学生学业平均成绩为样本进行计算，得到：

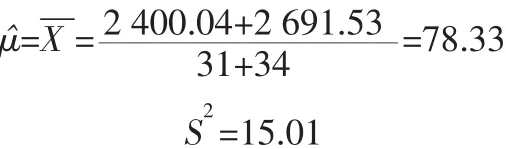
用同样的方法和样本计算毕业论文成绩的均值与方差。为便于计算，把优秀等级折合分数为95分，良好折85分，中等折75分，及格折65分。折合后的分数如表6所示。

表6 国贸03-1、03-2班毕业论文成绩等级折合分数

同样计算可得：

可以看出，毕业论文成绩均值83.62比学业平均成绩均值78.33明显要高，表明现行毕业论文成绩评定方法提高了毕业论文成绩；毕业论文成绩方差19.19比学业平均成绩方差15.01明显要大，表明现行毕业论文成绩评定方法拉大了成绩差距。

4 结束语

在认为经管类学生学业平均成绩和毕业论文成绩近似服从正态分布的基础上，对现行毕业论文成绩评定方法的有效性进行检验。结果表明学生学业平均成绩概率分布与其毕业论文成绩概率分布的差异是显著的，说明现行毕业论文成绩评定方法的有效性是值得怀疑的。进而采用最大似然估计法计算学生学业平均成绩与毕业论文成绩的均值与方差，结果表明毕业论文成绩均值和方差均比学业平均成绩大，说明现行毕业论文成绩评定方法提高了毕业论文成绩，拉大了成绩差距。因此，这种毕业论文成绩评定方法不能反映学生真实学业成绩，也显得不够科学合理而需要改进。

[1]傅应强，马森，康潘星,等.提高应用化学专业毕业论文（设计）质量的探索与实践[J].兰州教育学院学报，2016,32(8):91-92.

[2]孙宗玖，李培英，吴咏梅,等.新疆农业大学草学专业本科毕业论文质量的综合评价[J].黑龙江畜牧兽医，2016(9上):248-250.

[3]刘引涛.基于BP神经网络的毕业设计综合评价体系的研究[J].电子测试，2013(13):147-148.

[4]张嫣红，倪晓宇，刘英,等.本科生毕业设计（论文）质量评价体系研究[J].中国教育技术装备，2016(20):80-84.

[5]龚峰，陈明锐.基于层次分析法的本科毕业论文（设计）的质量评价研究[J].电脑知识与技术，2014,10(4):769-771.

[6]张瑾，郑李彬，孙多青,等.基于熵的高校大学生毕业论文（设计）质量的模糊综合评价法[J].高等教育研究，2011,28(3):8-11.

[7]李萍.高校学生考试成绩分布的正态性检验[J].陕西教育学院学报，2013,29(1):96-98.

[8]张志莉.正态分布在考试成绩评定中的应用[J].呼伦贝尔学院学报，2011,19(5):111-113.

[9]杨海波，杨海燕，于荣娟,等.假设检验在成绩分析中的应用[J].内蒙古农业大学学报（自然科学版），2015,36(5):149-153.

[10]余水.学绩测验分数分布形态及其应用研究[J].贵阳学院学报（自然科学版），2016,11(1):31-34.

[11]马玉秋，曹丽华，曹诺.基于SPSS的大学生学期成绩正态性检验分析[J].才智，2014,35(3):123-124.

[12]王云，袁旭华，彭凡,等.基于SPSS对学生成绩的分析研究[J].延安大学学报（自然科学版），2015,34(4):33-36.

[13]杜美萍.关于高职院校学生成绩分析与预警的思考[J].科教导刊，2016(4):184-186.

[14]张文杰.新升本科院校学生的学业成绩分布刍议[J].齐齐哈尔师范高等专科学校学报，2015(2):27-28.

[15]殷雷.学习态度与学习成绩的相关研究[J].心理科学，2008,31(6):1471-1473.

[16]盛骤，谢式千，潘承毅.概率论与数理统计[M].3版.北京：高等教育出版社，2002:147,185-186,241-243,443.