适用于云环境的LASVM异常检测研究
王瑞晗,高建瓴,陈 语
(1.贵州大学 大数据与信息工程学院,贵州 贵阳 550025;2.贵州大学 档案馆,贵州 贵阳 550025)
由于云计算模式能够对分散的、异构系统中的档案数字资源、计算资源进行有效集成和共享,开发新型的存储与计算共享架构,能够建立起区域内联动的运行机制[1]。所以目前已经有越来越多的档案馆将其业务运行在云平台上,不仅可以节省资金,减少工作量,并且能够更好地共享资源。作为负责为业务系统提供计算和存储资源且保证业务系统能够正常运行的虚拟机是云平台的基础是其核心部件[2],所以为了预警保障云平台的稳定运行,对虚拟机异常进行检测是其中重要的措施。由于传统SVM不能处理海量数据,且不具备在线学习能力,不能进行实时分类,所以不能满足云环境下的异常检测要求,所以文章使用具备在线学习能力且需求更少内存能够处理海量数据的LASVM算法来进行异常检测。
1 支持向量机
1.1 支持向量机原理
作为一种流行的机器学习算法,支持向量机[3](Support Vector Machines,SVM)在模式识别、回归分析、函数估计、时间序列预测等领域都得到了长足的发展[4],它是以统计学习理论[5-6]VC维理论和结构风险最小化原理为基础的。
支持向量机是一种二类分类模型,它是在感知器(Perceptron)基础上发展而来,可以表述为以特征空间上的间隔最大的线性分类器为其基本模型,以最大化间隔为其目的,最终转化为一个凸二次规划问题的求解[3]的机器学习方法。
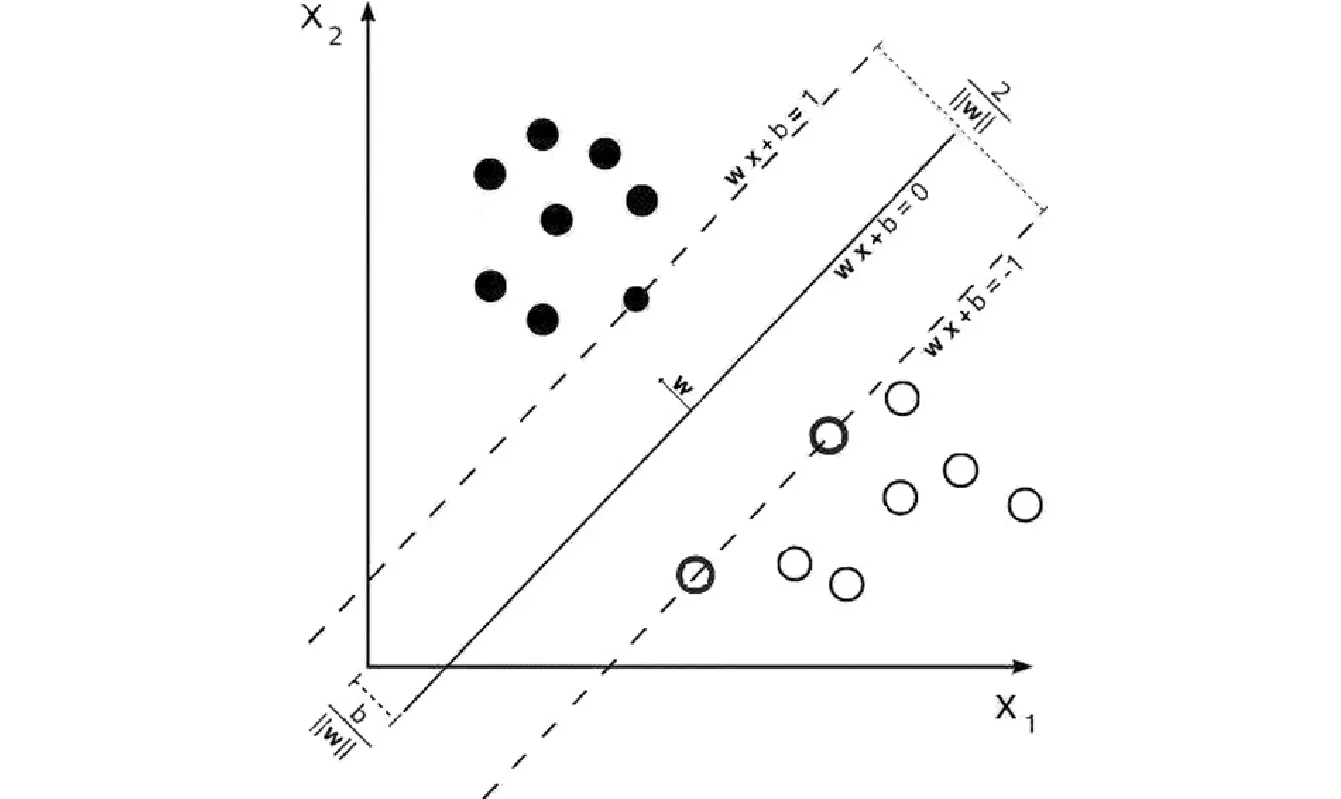
图1 超平面间隔示意
f(x)=sgn(wTx+b)
(1)
根据几何知识,wTx+b=+1和wTx+b=-1两个平行超平面间的间隔为2/‖w‖,此时其数学模型类似地描述为
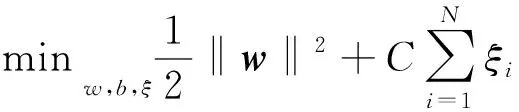
(2)
其中,ξi(ξi≥0)为松弛因子;C为惩罚因子;φ(x)为非线性情形下的映射函数。这是一个典型的凸二次规划。利用最优化知识,引入Lagrange函数
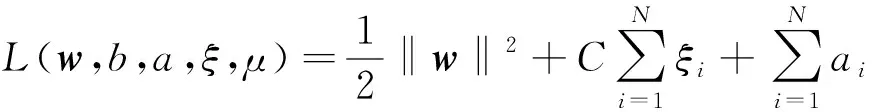
(3)
其中,αi≥0,μi≥0是Lagrange乘子。
引入核函数K(xi,xj)=φ(xi)·φ(xj)来代替内积xiTxj,可得其对偶规划为
(4)
1.2 SMO算法
标准SVM训练算法可以归结为求解一个具有线性不等式约束的二次规划(Quadratic Programming,QP)问题。历来解决式(4)的二次规划问题是构造支持向量机的核心问题,在Osuna[7]等提出的使用一系列小规模的子QP问题替代标准SVM的QP问题的分解算法基础上,由微软研究院的John Platt[8]发明的序列最小优化(Sequential Optimal Minimization,SMO)算法被认为是解决SVM问题的最优秀算法之一。它将问题分解为一系列只含有两个变量的最小QP问题,避免了一般二次规划方法过大的空间需求,使实现变得简单高效。
为了方便,令αiyi→αi,可将式(4)的对偶规划写作
(7)
SMO算法类似Vapnik[10]提出的共轭梯度法,都是通过不断的搜索,来寻求最佳的下降方向。每个方向搜索都是通过当前的向量α和增加的指定方向u。从而产生一个新的弹性向量α+λu,所以其最优解为
λ*=argmaxW(α+λu)
s.t. 0≤λ≤φ(α,u)
(8)
其中,上边界φ(α,u)确保α+λu是可行的,表达式为
(9)
对式(8)中的向量α分别求每个方向的导数,则可得到最优解
(10)
其中,Kij=K(xi,xj),gk=∂W(α)/∂αk=yk-∑iαiK(xi,xk)是W(α)的梯度。
SMO的基本思路是每次迭代过程中只调整相应的两个样本点的αi和αj。通常使用一个微小的正容忍度τ>0,选那些使得φ(α,u)>0并且gi-gj>τ的u。这样可以定义叫做τ违反对(i,j)
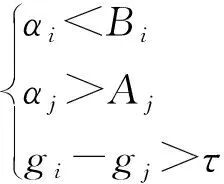
(11)
SMO算法的流程如下:
(1)将α设置为0,并且计算初始梯度g;
(2)选择一个τ违反对(i,j),若不存在则跳出程序g;
(3)λ←min{(gi-gj)/(Kii+Kjj-2Kij),Bi-αi,αj-Aj}
αi←αi+λ,αj←αj-λ
gs←gs-λ(Kis-Kjs) ∀s∈S
(4)重复步骤(2)。
2 在线主动LASVM
由于传统SVM不能处理海量数据集,除了在降低传统QP问题求解的复杂度的研究外,还有研究者提出了一些新的优化方法,比如使标准SVM具备增量学习(Incremental Learning)算法的能力[9-10]。亦即是使用增量学习中的在线学习(Online Learning)来改善标准支持向量机在遇到当训练集规模很大时,出现的训练速度慢、算法复杂、效率低,且在初期就获得一个完备的训练数据集是很困难的问题。
LASVM[11]算法是由Bordes和Bottou最早提出的,它是一种采用传统软间隔模型,对SMO算法中挑选α对的过程进行变形的一种算法。它有两个潜在的优势,首先它能够在线学习和主动学习,其次SVM对于大数据集的计算需要大量时间,近似算法处理速度更快,占用内存更少,更适合处理大数据集。
这种方法由称之为PROCESS和REPROCESS的两种方向搜索步骤构成。和SMO算法相似,每种方向搜索每回都只选取两个样本。PROCESS至少能够选择一个当前判别式的非支持向量,它可以改变这个样本的α值,使其成为支持向量将其加入支持向量集。REPROCESS处理当前判别式中的两个支持向量,它可以将一个或者两个支持向量的α值改为0,从而使其不再成为支持向量,然后将其移出。
对于PROCESS步骤,其目的是试图添加一个样本k∉S到当前的支持向量集中。其具体的步骤如下
(1)如果k∈S样本,那么跳出程序;
(2)αk←0,gk←yk-∑s∈SαsKks,S←S∪{k}
如果yk=+1,那么i←k,j←arg mins∈Sgs且αs>As;
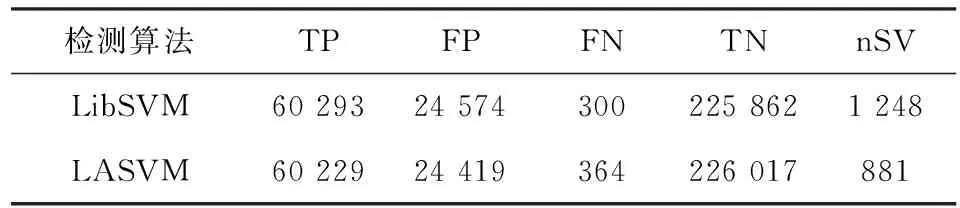
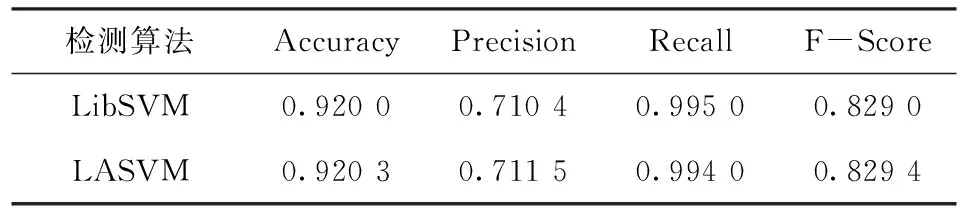
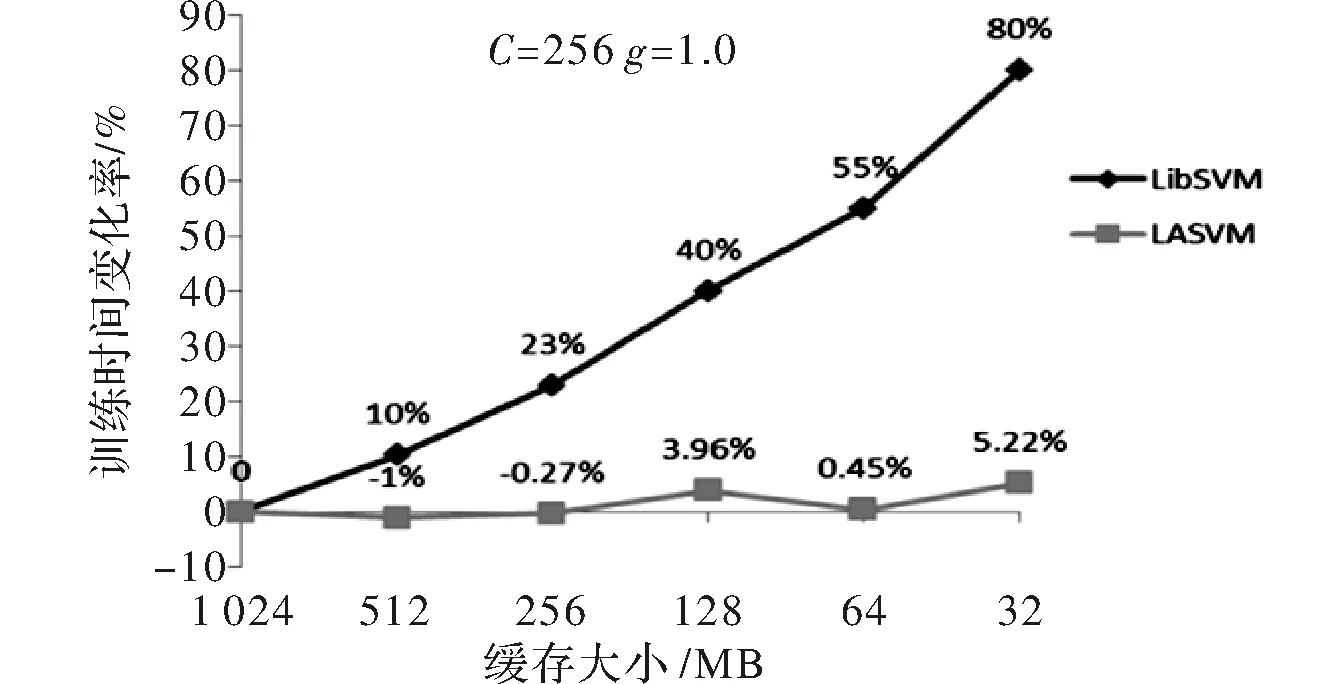
如果yk=-1,那么j←k,i←arg maxs∈Sgs且αs (3)如果(i,j)不是一个τ违反对,那么跳出程序; (4)λ←min{(gi-gj)/(Kii+Kjj-2Kij),Bi-αi,αj-Aj} αi←αi+λ,αj←αj-λ gs←gs-λ(Kis-Kjs) ∀s∈S。 第二个步骤是REPROCESS,其目的是从S集中移除某些元素。具体的步骤如下 (1)i←arg maxs∈Sgs且αs j←arg mins∈Sgs且αs>As; (2)如果(i,j)不是一个τ违反对,那么跳出程序; (3)λ←min{(gi-gj)/(Kii+Kjj-2Kij),Bi-αi,αj-Aj} αi←αi+λ,αj←αj-λ gs←gs-λ(Kis-Kjs) ∀s∈S; (4)i←arg maxs∈Sgs且αs j←arg mins∈Sgs且αs>As 对于s∈S中所有αs=0的向量 如果ys=-1且gs≥gi,那么S=S-{s} 如果ys=+1且gs≤gj,那么S=S-{s}; (5)b←(gi+gj)/2,δ←gi-gj。 有了PROCESS和REPROCESS模块后,可以搭建LASVM的总体框架,具体的算法流程如图2所示。 LASVM除了可以在线的进行训练,即在每给出一个连续的实时随机样本时,都会更新内部支持向量以及其参数外。LASVM也可以在样本集充足的情况下,作为一个批量学习的优化算法,每次随机地抽取一个样本作为训练样本进行训练。 图2 LASVM流程图 该数据集是哥伦比亚大学的Sal Stolfo教授和来自北卡罗莱纳州立大学的Wenke Lee教授采用数据挖掘等技术,对美国国防部高级规划署(DARPA)在模拟美国空军局域网网络下仿真各种用户类型、各种不同的网络流量和攻击手段收集的TCP dump(*)网络连接和系统审计数据集进行了特征分析和数据预处理后形成的一个数据集。该数据集分为了大概500万条网络连接记录的训练集和大概200万条网络连接记录的测试集。在1999年举行的KDD CUP竞赛中被用于比赛,成为著名的KDD99数据集[12]。KDD99数据集在基于计算智能的网络入侵检测研究中常作为网络入侵检测领域的事实基准,当做标准数据集使用。 由于原数据集过于庞大,随机选取10%数据集作为实验数据,原数据集包含包含4类攻击和正常标签,由于主要进行异常检测,不需要知道具体异常类型,本文使用了二分类,所以将所有正常和异常数据分别标记为+1和-1,如表1所示。 表1 归一化后的训练数据集类别和样本数 KDD-CUP99数据集每条数据有41个属性,其中34个是连续型变量,7个是离散型变量,其中protocoI_type、service、fIag3个属性为标称属性,首先要对其进行数值化处理。又由于每个属性的取值范围不同,且取值范围都为正,所以再进行范围为0~1的归一化处理,从而避免了不同量纲的选取对计算产生的巨大影响。 当面临不平衡数据集的时候,机器学习算法倾向于产生并不令人满意的分类器[13]。显然在总共494 021条数据中,正常样本只占大约19.7%,是一个典型的不平衡数据集,会影响训练出的分类器的性能,本文采用重采样技术中的随机过采样方法处理训练数据集,通过随机复制正常标签数据来增加正常实例数量,从而平衡数据集,最终形成正常数据和异常数据各396 743条总共793 486条数据的训练数据集。 惩罚因子和核函数中的参数是影响支持向量机性能的主要参数,因为文章的核函数使用径向基核函数(Radical Basis Kernel Function,RBF核)K(xi,xj)=exp(-gamma×‖xi-xj‖2),所以需要寻找合适的惩罚因子C和RBF核函数中的控制因子g=1/σ2。 本文使用网格搜索法(Grid Search Algorithm,GSA)来进行参数寻优,网格搜索法是一种最基本的参数优化算法,适合同时从不同的增长方向并行搜索多维数组。具体流程图如图3所示[14]。 图3 基于网格搜索算法的SVM参数寻优流程图 使用分层抽样的方法从训练数据集中抽取50 000条数据使用网格搜索的方法进行参数寻优。设置惩罚因子C和RBF核函数中的控制因子g的范围分别为2-15≤C≤215,2-15≤g≤215,步长C_step=0.5,g_step=0.5,采用K=10的10折交叉验证方法。 通过训练最终得到当C=256,g=1.0时准确率最高,即为最优参数。同时得到训练出的不同参数值下的准确率梯度图,如图4所示。 图4 参数C和g的准确率梯度图 实验硬件环境是Intel(R) Xeon(R) E7 2.00 GHz CPU,8 GB RAM,软件环境基于VMWare虚拟机下的CentOS 7操作系统,以VISUAL C++ 2010实现LASVM算法,支持向量机选用C-SVM,核函数选用径向基函数,其中C=256,g=1.0。 LibSVM[15]是由台湾大学林智仁(Lin Chih-Jen)教授等开发设计的目前广泛使用的经典离线学习SVM包,它使用SMO算法解决QP问题。所以选用LibSVM作为对比,从准确性、内存占用量等方面验证LASVM算法的效果。其中异常检测系统的评价标准如下: 精确度(Accuracy)是指所有正确检测出来的正常和异常记录在总样本中所占比例,表示为 (12) 查准率(Precision)是指被检测出来的真正是异常记录的数目在总的入侵记录中所占比例,表示为 (13) 查全率(Recall)是指真正的攻击记录中被检测出来的占所有攻击记录的比例,表示为 (14) F-Score是Precision的Recall的调和平均数,是用来评估一个检测系统好坏的度量,表示为 (15) 使用之前平衡过的训练集和测试集进行实验,实验结果如表2~表4所示。 表2 LibSVM与LASVM检测结果比较(C=256,g=1.0) 表3 LibSVM与LASVM检测性能比较(C=256,g=1.0) 表4 libSVM与LASVM进程占用的物理内存比较(C=256,g=1.0) 从表2和表3可以看出,与LibSVM相比,LASVM的混淆矩阵TP、FP、FN、TN的差距分别是-0.14%、-0.63%、21.33%、0.07%,即二类错误率稍高,其他接近LibSVM。Accuracy、Precision、Recal、F-Score的差距分别为0.03%、0.11%、-0.10%、0.04%,和LibSVM基本一致,都能够达到较好的分类效果,但其支持向量数量更少。 从表4可以看出,在对同一个数据集进行训练时,设置同等大小缓存情况下,由于LASVM具备在线学习能力,不需要一次性将整个数据集加入内存进行训练,所以占用的物理内存量要比LibSVM少89.17%。且由图5可以看到在以1 GB缓存为基点的对比不同缓存大小情况下的训练时间变化上,LASVM算法在不同缓存大小情况下,训练时间变化率不大,对内存资源的要求更低。由于LASVM算法对物理内存的消耗更少,且可在较少缓存下即可实现较快的训练速度,所以LASVM算法对于海量数据集有更好的适应性。 图5 LibSVM与LASVM在不同缓存大小情况下训练时间的变化 实验表明,LASVM算法在具备良好分类效果的同时,还能处理更大的数据集,且对内存资源的消耗更少,还具有在学学习能力,能够进行实时检测的优点。 通过理论分析和对网络数据的实验验证,说明LASVM算法对大数据集具有较好的分类性能的同时,对内存的需求更低,并且还能够进行在线和主动学习,达到实时处理数据的目的。较之普通SVM算法,能够更好地适用于在云环境下检测虚拟机异常。下一步工作,将使用LASVM算法对真实云环境下采集到的虚拟机性能指标数据集进行测试并进一步改进以提高检测精确度。 [1] 祝庆轩,桑毓域,方昀.基于云计算的档案信息资源共享模式研究[J].兰台世界,2011(15):8-9. [2] 王桂平.云环境下面向可信的虚拟机异常检测关键技术研究[D].重庆:重庆大学,2015. [3] 克里斯蒂亚尼尼,Johnshawe-Taylor.支持向量机导论:英文版[M].北京:机械工业出版社,2005. [4] 吉卫卫,谭晓阳.SVM及其鲁棒性研究[J].电子科技,2012,25(5):97-100. [5] 瓦普尼克.统计学习理论[M].北京:电子工业出版社,2015. [6] Vapnik V. Statistical learning theory[M].London:DBLP,2010. [7] Osuna E,Freund R,Girosi F.An improved training algorithm for support vector machines[C].Germany:Neural Networks for Signal Processing,IEEE Xplore,1997. [8] Platt J C.Fast training of support vector machines using sequential minimal optimization[M].MA,USA:MIT Press,1999. [9] Li Z Y,Zhang J F,Hu S S.Incremental support vector machine algorithm based on multi-kernel learning[J]. 系统工程与电子技术:英文版,2011,22(4):702-706. [10] Nguyen-Tuong D,Peters J.Incremental online sparsification for model learning in real-time robot control[J].Neurocomputing,2011,74(11):1859-1867. [11] Bordes A,Ertekin S,Weston J,et al.Fast kernel classifiers with online and active learning[J].Journal of Machine Learning Research,2005,6(6):1579-1619. [12] 张新有,曾华燊,贾磊.入侵检测数据集KDD CUP99研究[J].计算机工程与设计,2010,31(22):4809-4812. [13] 吴磊,房斌,刁丽萍,等.融合过抽样和欠抽样的不平衡数据重抽样方法[J].计算机工程与应用,2013,49(21):172-176. [14] Wang J,Zhang L,Chen G.A parameter optimization method for an SVM based on improved grid search algorithm[J].Applied Science & Technology,2012(3):28-31. [15] Lin C H,Liu J C,Ho C H.Anomaly detection using LibSVM training tools[C].Beijing:International Conference on Information Security and Assurance,IEEE,2008.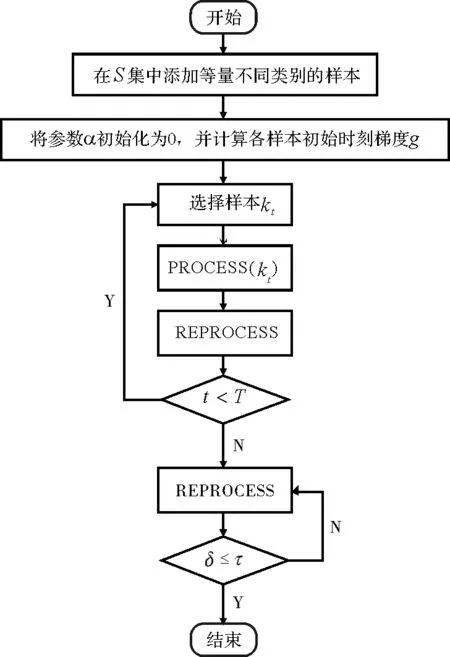
3 不平衡数据集处理
3.1 KDD-CUP99数据集
3.2 归一化(Normalizatio)
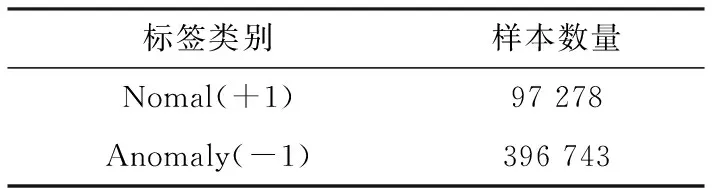
3.3 过采样(Over-Sampling)
4 应用LASVM方法的入侵检测实验
4.1 基于网格搜索算法的参数优化
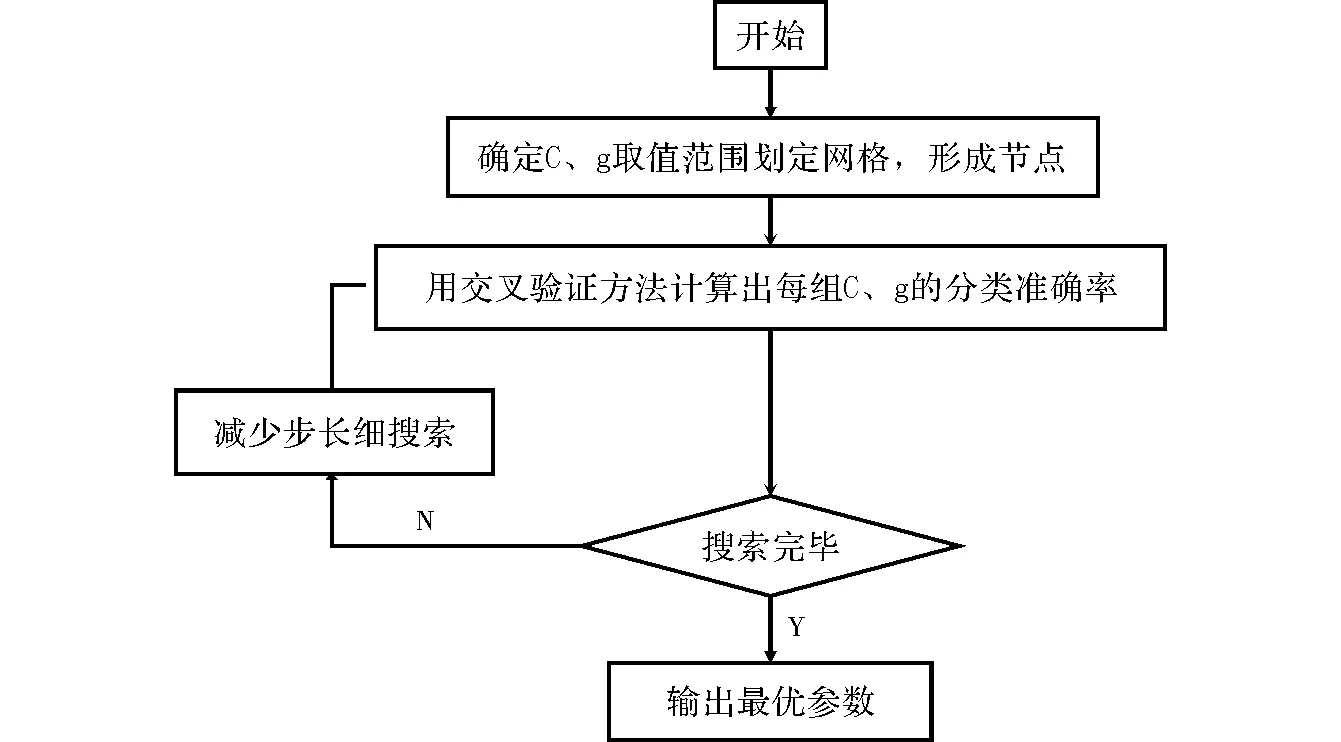
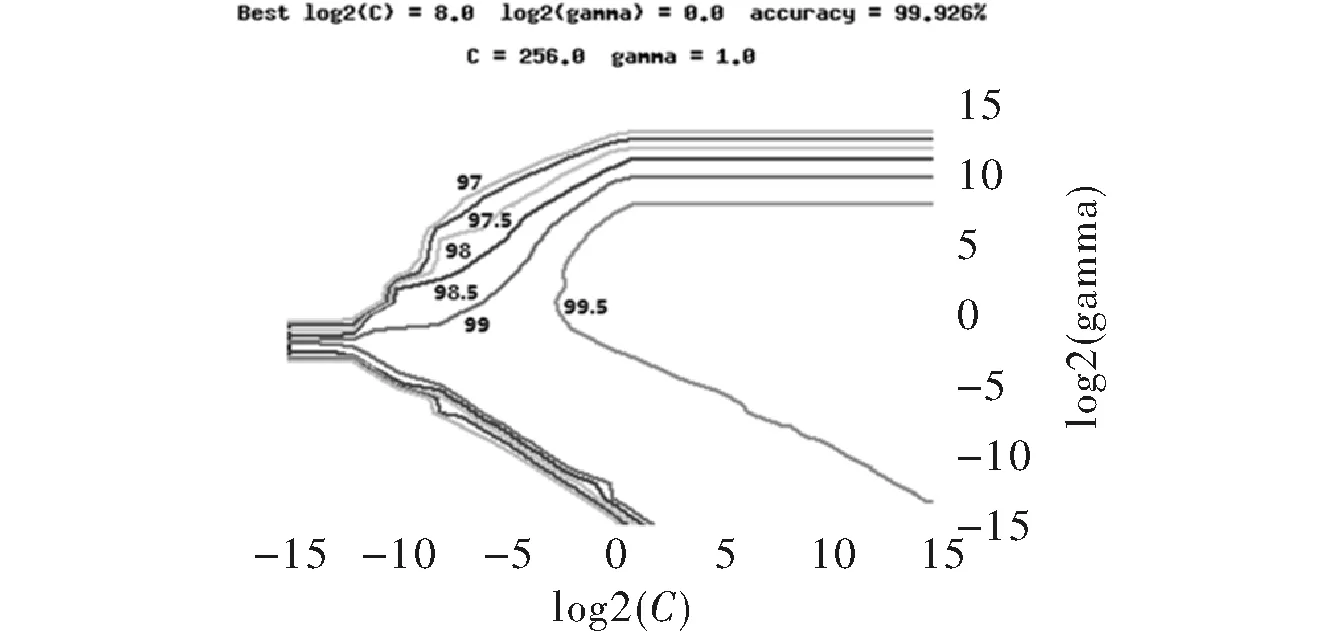
4.2 LASVM和LibSVM的对比实验

5 结束语

