基于变论域模糊PID的垂直提升系统控制研究

孙伟翔，汪旭东，许孝卓，封海潮

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

在现代高层建筑的不断增多的情况下，使用传统旋转电机作为驱动机构的提升系统已经无法满足人们的要求。随着直线电机技术在国内外发展的日趋成熟，且永磁同步直线电机(Permanent Magnet Synchronous Linear Motor，PMLSM)在垂直提升系统的结构上已经实现了“无钢丝绳、无配重、无中间传动装置、无提升速度限制、无提升高度限制”的“五无”提升模式，具有安全性能好，整体效率高，提升能力大，适应恶劣环境，可实现多轿厢同时运行的优点[1]，使得很多专家将直线电机技术运用到高层建筑的提升系统中来。在提升系统中永磁同步直线电机是构成直驱技术的核心，但由于PMLSM本身的非线性、多变量、强耦合等因素而使提升系统容易受到很多自身及外界的干扰[2-3]。为减少干扰，提高系统的控制精度，诸多研究专家采用了例如：神经网络控制、迭代学习控制、专家控制等方法对垂直提升系统的PMLSM进行控制，也都取得了一定的效果。为了解决一些不良因素对垂直提升系统的干扰，本文设计了可变论域的模糊PID控制器对PMLSM垂直提升系统的驱动机构进行控制。结果表明可变论域的模糊PID控制器可以更好的改善垂直提升系统的控制精度及鲁棒性。

1 PMLSM垂直提升系统结构及模型

1.1 PMLSM垂直提升系统的结构

整个PMLSM垂直提升系统的结构由初级电枢绕组、动子、轿厢等组成。为保证系统中电机初级与电机动子永磁体之间的耦合磁场面积的恒定，该结构要求动子的纵向长度为2台初级与2段间隔长之和[4]。PMLSM垂直提升系统结构如图1所示。

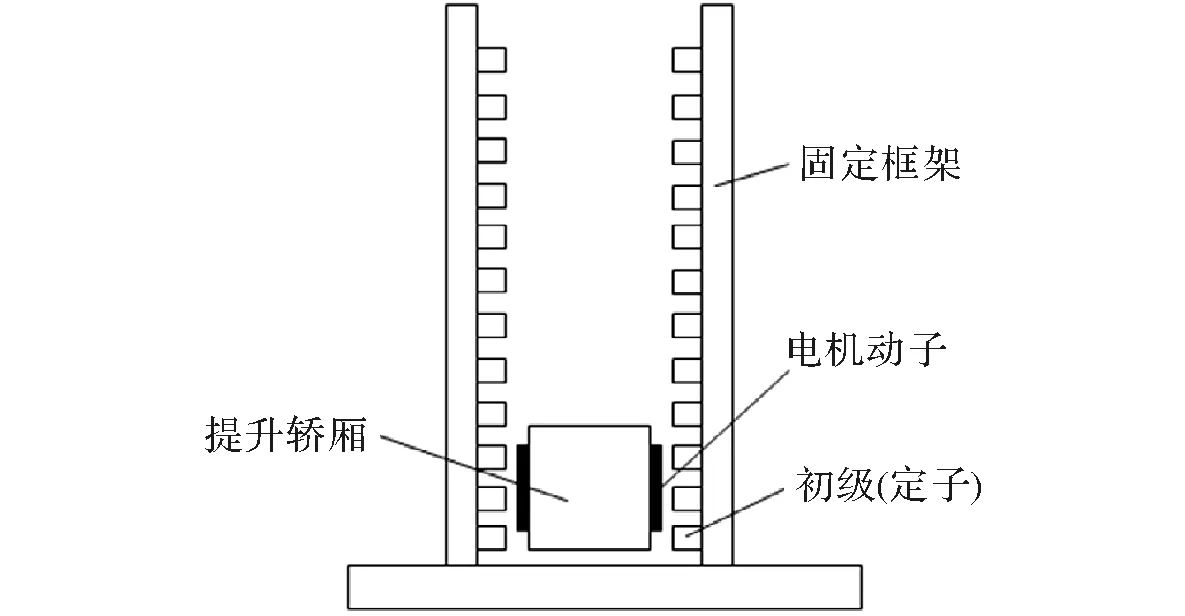
图1 PMLSM垂直提升系统结构

1.2 垂直提升系统PMLSM的数学模型

在建立PMLSM的数学模型之前，首先作以理想条件下的假设[5-6]：(1)忽略温度及铁心饱和对电机性能参数的影响；(2)忽略涡流和磁滞损耗；(3)不计初级阻尼作用和纵向端部效应；(4)永磁体电导率为零且磁场恒定。

永磁同步直线电机d-q轴电压方程

(1)

(2)

式中，V是电机的速度，τ是极距，R为电枢电阻，φf是永磁体磁链，Ld和Lq分别为直轴、交轴电感，Ud和Uq分别为直轴、交轴电压，id和iq分别是直轴、交轴电流。

在无任何外力的情况下，输入功率为

(3)

进而推导出电磁推力方程

(4)

永磁同步直线电机的机械平衡方程

(5)

其中φd和φq分别为d与q轴磁链，Fd是负载阻力，Fe是电磁推力，Bv为粘性摩擦系数，M是直线电机质量。

由上述数学表达式可以得出永磁同步直线电机的结构框如图2所示。

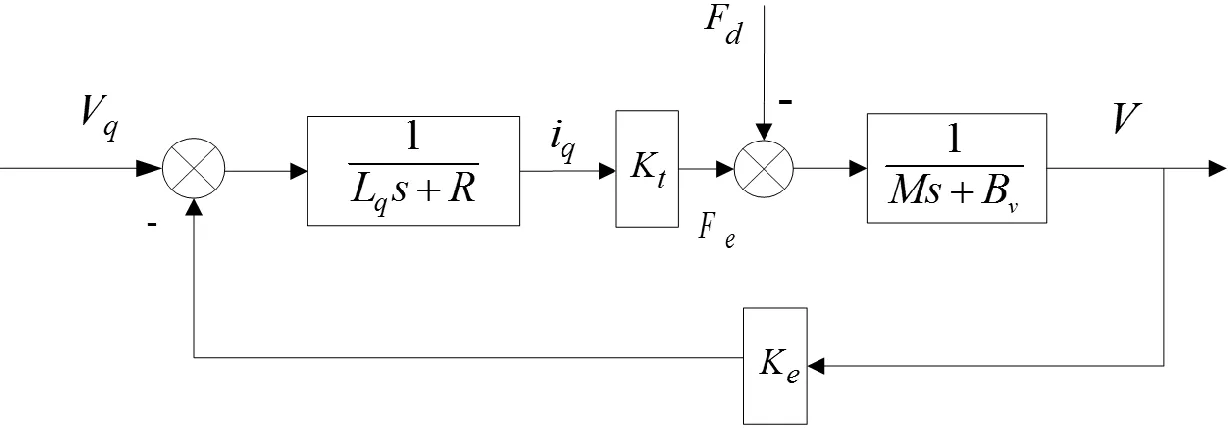
图2 永磁同步直线电机结构框图

2 变论域模糊PID控制器设计

2.1 变论域模糊PID控制器的结构

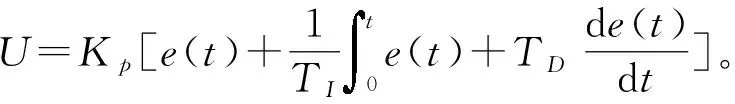
模糊控制建立在人类思维模糊性的基础上[9]，是目前控制领域中最具实际意义的智能控制方法之一。变论域模糊PID控制器是在传统PID控制器的基础上，增加论域调整、模糊推理思想等模块。在该控制器中将被控量的偏差e及其变化率ec作为模糊控制器的输入变量，通过模糊控制器的输出变量去整定PID各参数，进而构成可变论域的模糊PID控制系统，系统结构如图3所示。

图3 变论域模糊PID控制结构图

2.2 输入输出论域、伸缩因子的选择

变论域模糊PID控制器通过伸缩因子来调整初始论域[10]。设输入误差e及其变化率ec的基本论域为Xi=[-E,E],其中i=1,2时Xi分别为e、ec的基本论域。Kp、KI、Kd为输出变量，基本论域表达为Yj=[-U,U],其中j=1,2,3时Yj分别对应输出变量Kp、KI、Kd的基本论域。引入伸缩因子，则系统输入的变化论域分别为

(6)

其中α(x)和β(x)为伸缩因子，可用式(7)求出。

γ(x)=1-λe-kx2，0<λ<1，k>0

(7)

2.3 模糊规则的确定

PID参数的整定必须考虑不同时刻3个参数的作用及其相互之间的关系[11-12]。针对不同的e和ec，利用模糊规则整定PID的3个参数要符合以下原则：

(1)当|e|较大时，应取较大Kp和较小的Kd，以使系统响应加快；

(2)当|e|中等时，应取较小Kp及适当Kd、KI，以使系统具有较小超调；

(3)当|e|较小时，应取较大Kp和KI以及适当的Kd，避免在平衡点附近出现振荡，使系统稳态性能更优[13-15]。

综上，确定输入e、ec以及输出ΔKp、ΔKI、ΔKd的模糊子集均为{NB NM NS Z PS PM PB}，其隶属度函数选用三角形函数，并采用Mamdani推理规则进行模糊运算，其中ΔKp、ΔKI、ΔKd的模糊规则如表1所示。

表1 ΔKp、ΔKI、ΔKd的模糊规则表

3 仿真分析

为了验证变论域模糊PID控制器对PMLSM垂直提升系统的影响，在 Matlab/Simulink中对可变论域的模糊PID控制器进行构建仿真，建立好的变论域模糊PID控制器如图4所示。

图4 变论域模糊PID控制器模型

图5 基于变论域模糊PID控制的PMLSM垂直提升系统的控制仿真图

如图6所示，是传统PID控制、模糊PID控制及变论域模糊PID控制分别对PMLSM垂直提升系统进行控制的速度响应仿真结果的对比。从速度仿真结果可以看出，传统PID控制的速度响应有超调且上升时间相对缓慢，而模糊PID控制及变论域模糊PID控制在速度响应上更加平稳，速度在上升期间没有超调和波动。相对于模糊PID控制，变论域模糊PID控制的速度响应更加迅速，可以更好的满足系统对速度高性能的要求。

图6 速度响应对比图

4 结束语

针对垂直提升系统的PMLSM存在非线性、参数摄动、负载扰动等问题，为改善系统对速度性能的较高要求，在传统PID控制的基础上，设计了可变论域的模糊PID控制器对PMLSM垂直提升系统的速度进行控制。将不同控制下的速度响应结果进行对比，可以看出变论域模糊PID控制相较于传统PID控制、模糊控制能够更好的改善系统对速度的性能要求，具有较强的实用价值

[1] 汪旭东,封海潮,许宝玉,等.PMLSM垂直提升系统的应用研究[C].焦作:2010年全国直线电机、现代驱动及系统学术年会,2010.

[2] 李爱平,邓海洋,徐立云.基于模糊PID的永磁同步电机矢量控制仿真[J].中国工程机械学报,2013,11(1):25-30.

[3] 王泽,李泽滔,张佳荣,等.永磁同步电机模糊PID控制器的研究[J].机械与电子,2012(8):30-33.

[4] 张宏伟.永磁直线同步电动机垂直运输系统控制策略与控制装置研究[D].焦作:河南理工大学,2005.

[5] 沈建清,吴世君,翟小飞.高精度永磁同步直线电动机Matlab仿真[J].微电机,2008,41 (6):76-78.

[6] 赵吉文,王荔枝,张梅,等.直线电机动子位置检测的图像亚像素测量算法[J].仪器仪表学报,2013,34(11):592-598.

[7] 丁文双,胡育文,鲁文其,等.永磁同步电机模糊PID参数自整定[J].微特电机,2011(5):17-21.

[8] 于水乐,高霖.永磁同步电机模糊PID控制的建模与仿真[J].航空制造技术,2012(20):92-94.

[9] 蔡淑敏,王亚刚,田涛.智能控制算法研究及Matlab实现[J].电子科技,2016,29(7):43-46.

[10] 李洪兴,苗志宏,王加银.非线性系统的变论域稳定自适应模糊控制[J].中国科学:E辑,2002,32(2):211-223.

[11] 翟小飞,张俊洪,赵镜红.永磁同步直线电机的Matlab仿真及其定位试验[J].船电技术,2006(4):6-9.

[12] Hua Sun,Dai Yuehong.Fuzzy PID control and simulation experiment on permanent magnet linear synchronous motors[J].CA,USA: International Conference on electrical and Control Engineering,2010.

[13] 戴雅丽.基于遗传算法优化模糊控制器的船舶航向控制[J].船海工程,2009,38(3):113-115.

[14] Lin Changlong,Feng Xisheng,Gong Peiliang,et al.An application of the improved hybrid fuzzy PID control system[C].Chongqing:Proceeding of the 7m World Congress on Intelligent Control and Automation,2008.

[15] 谢仕宏.Matlab R2008控制系统动态仿真[M].北京:化学工业出版社,2009.