嵌入式系统下混沌加密算法研究

李良

（火箭军士官学校，山东 青州 262500）

0 引言

通信技术在给人们带来便利的同时，也给通信安全带来了一定的问题，比如一些非法接入及宽带数据、语音视频数据泄密等。信息安全问题俨然成为当今社会面临的一个重大问题，对企业或个人都是如此，因此对通信过程中秘密信息实现信息保护变得越来越重要。由于混沌信号的独特性，通过嵌入式通信设备产生可附加到有效通信信号中的混沌信号，实现对数据信息的混沌加密[1]是目前通信领域研究热点问题之一。

1 混沌的特性

人们发现混沌已经很长时间了，混沌现象一直存在于现实世界中。对混沌现象熟悉到利用的过程是逐渐探索进步的过程，这不仅是对物理学科认识的补充，也是对一些现象的重新认识。随着研究的深入，混沌的一系列特点和本质的被进一步的揭示和完善，对混沌完整的、具有实质性意义的确切定义还没有产生。目前人们还是把混沌定义为一种无序中的有序。它主要有以下特征[2]：

（1）轨迹从不重复。系统在经过一段时间的运动后，所产生的运动轨迹从不重复，其运动行为表现出了较强的类随机性，但又有迹可寻。

（2）展现出分形特点和数目不等的吸引子。当运动时间趋向于无穷大时，系统最终的状态归宿称为吸引子。

（3）对初始条件改变的较强敏感性。这是混沌行为非常显著的一个特性，许多的通信控制就是利用混沌的这种特性。混沌现象是非线性确定性系统中的伪随机的过程，把两个相近的初始值代入同一个迭代方程中，经过有限次的迭代即可使这些数值序列变得毫不相关，看上去好像很乱，没有结构层次，其实从其本质来看是有迹可寻的，是颇有规律的。混沌信号的类噪声、宽频谱以及混沌信号的非周期性，都使它具有极高的隐蔽性，这些特性对于实现混沌加密技术以及设计算法是非常有好处的。

2 嵌入式系统下混沌加密算法研究

嵌入式通信设备（比如移动电话、平板电脑等）已经成为人们学习工作不可缺少的一部分，在嵌入式系统环境下求解混沌动力学方程产生混沌信号并将其应用于保密通信中的研究意义是非常重大的。

2.1 数值算法分析

利用龙格-库塔方法对常微分求数值解[3]是一种在工程技术领域上应用比较普遍的算法。它的计算精度比较高，与欧拉法一样的是都属于单步算法。即计算下一步时，只用到前一步值。龙格库塔算法的实现是建立在数学支持的基础之上，它的推导过程与泰勒级数法有密切的关系。本文采用四阶龙格-库塔公式对混沌动力学方程进行求解分析。四阶龙格-库塔方法的一般公式表达式为方程组1所示：

进一步可以推导出常用四阶龙格-库塔公式，为方程组2所示：

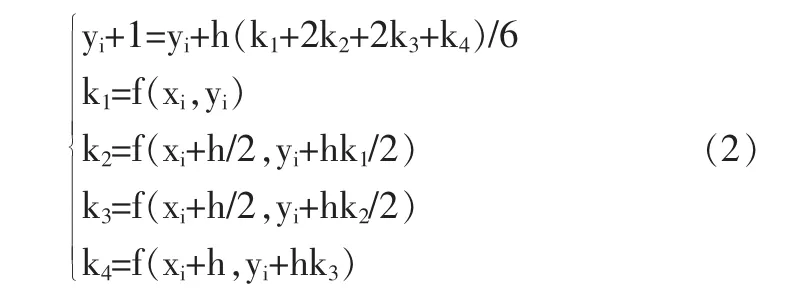
2.2 嵌入式系统环境下混沌动力学方程求解步骤

本文中采用的嵌入式Linux操作系统版本为Linux-2.6.30.4，交叉编译器版本为EABI-4.3.3。嵌入式操作系统的主要工作是实现对存储介质管理和存储介质空间地址分配，对各进程进行管理，在运行时转入处理各种中断等[4]。嵌入式系统环境下微分方程求解步骤如下：

（1）首先在Linux嵌入式系统的VIM编辑器环境下，按照龙格库塔推导思想对微分方程数值求解程序进行编写。

（2）编写完成之后，对所编写程序进行交叉编译。

（3）把交叉编译生成的可执行文件下载到实验板中执行，下载可执行文件前提是uboot以及Linux系统的映像文件已下载至硬件设备。

（4）修改可执行文件的权限。

（5）把可执行文件放到android系统下的数值分析软件中进行分析。

3 用龙格库塔算法求解信号发送端的混沌电路模型

通信信号的发送端混沌电路模型采用在物理学报上提出了一种新的网格多翅膀混沌系统[5]。这种新系统提出与实现与其它三维自治系统相比较，存在的相同点是都能够产生一个双翅膀的吸引子，那么存在的不同点是该新系统可以根据其双涡旋的吸引子拓扑结构，通过设定适合的非线性函数使之能够产生（2n+2）*（2m+2）网格的吸引子。通过非线性函数中的可调参数可以灵活的控制吸引子翅膀的数量、大小及相对位置。

经过硬件电路实验证明，当a=1，b=0.9，c=0.32时，上述新系统数学模型能够产生两个不稳定的平衡点的混沌行为状态。原方程可化为方程组3所示。

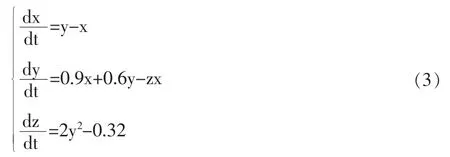
设状态变量初值 x（0）=y（0）=z（0）=0.1 时进行研究，步长为0.01，按照混沌动力学方程求解步骤进行求解并作图分析，观察混沌行为现象。图1为新系统模型在一定的初值条件下产生的混沌吸引子在x-y平面的投影。图2为混沌吸引子在z-x平面的投影。图3是混沌吸引子在z-y平面的投影，可以看出新系统产生了4网格的多涡旋混沌吸引子。

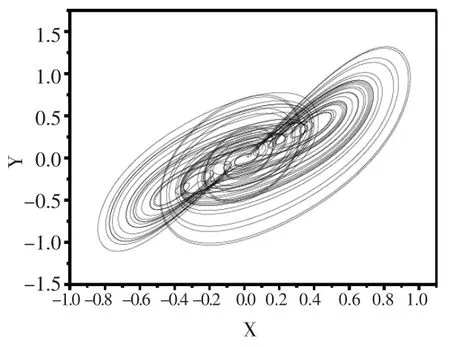
图1 吸引子在x-y平面的投影

图2 吸引子在z-x平面的投影

图3 吸引子在y-z平面的投影

4 结束语

本文通过对通信信号发送端混沌系统硬件电路的分析，实现了在嵌入式系统环境下对混沌系统模型求数值解，并对产生的混沌信号的特性进行了分析验证。下一步只要在信号发送端加入合适的调制信号，就可以实现混沌加密通信。

[1]冯久超.混沌信号与信息处理[M].北京：清华大学出版社，2012.

[2]David M.Harrison，An introduction to Chaos，2006.

[3]翟瑞彩，谢伟松.数值分析[M].天津：天津大学出版社，2000.

[4]林晓飞，刘彬，张辉.基于ARM嵌入式Linux应用开发与实例教程[M].北京：清华大学出版社，2007.

[5]周欣，王春华，郭小蓉.一个新的网格多翅膀混沌系统及其电路实现[J].物理学报，2005，20.