基于自适应稀疏组合学习的异常事件检测
谢森义,黄朝兵
(武汉理工大学信息工程学院,武汉 430070)
0 引言
随着社会的发展,安全监控越来越普及。由人工来鉴别这些监控视频效率是非常低而且人工成本也很高。这就加大了对视频异常事件检测的需求。目前,对于异常事件检测仍然没有一个精确的定义,大多数的检测方法都是对正常事件建模,不属于正常事件的所有事件都被认为是异常事件,这就需要训练数据包含更多的正常事件种类。
异常事件检测方法可分为基于目标轨迹的方法[1]和基于底层特征的方法。基于目标轨迹的方法对目标进行跟踪,提取目标轨迹进行异常检测。这种方法可以获取运动目标的各种状态,准确度高;缺点是局限于目标跟踪算法,对噪声、遮挡很敏感,在拥挤的场景中存在大量遮挡,跟踪效果较差。而基于底层特征的算法在拥挤场景中可以有良好的表现效果。目前经典的检测模型包括概率主题模型[2]和稀疏表示模型[3-4]等。稀疏表示第一次应用于异常事件检测时就表现出了良好的性能。但由于大量的计算没有取得很快的检测速度,远远达不到实时性的要求。
鉴于上述问题,本文采用了稀疏组合学习的检测模型[4]进行异常事件检测。并针对其不能自适应的问题作出改进。
1 异常事件检测流程
本文检测算法流程图如图1所示,本算法适用于拥挤场景,可以检测出局部异常事件。
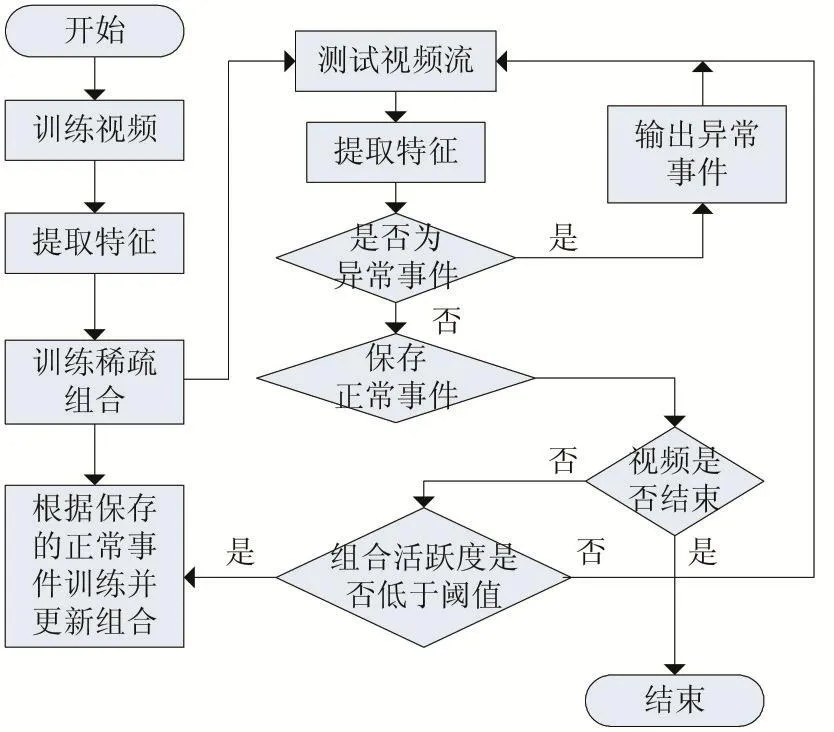
图1 异常事件检测流程
在特征提取阶段运动模型的表示采用时空模型[5],这样可以检测局部异常事件,模型特征采用三维梯度特征,为每一个时空容器提取三维梯度特征,通过PCA对特征降维。在离线训练阶段采用稀疏组合学习,学习出K个组合(K由训练视频决定),在视频的测试阶段,用学习出的K个组合检测异常事件,并根据组合的活跃度,利用当前正常特征训练并更新组合。
1.1 三维梯度特征
三维梯度是基于是时空运动模式模型[5]的。为了检测到局部异常事件,需为局部区域建立模型,在时空运动模型中,将视频分为空间和时间上都互不相关的区域,称之为时空容器。对于训练视频中的每个时空容器都提取对应的时空梯度特征,就可用于正常事件的建模。
如图2所示,先将视频的每一帧分为M*N块,再以相同空间位置连续5帧就构成了一个时空容器。

图2 时空模型
图2所示就是其中一个时空容器。对于每一个时空容器I中的第i个像素,时空梯度∇Ii定义为:
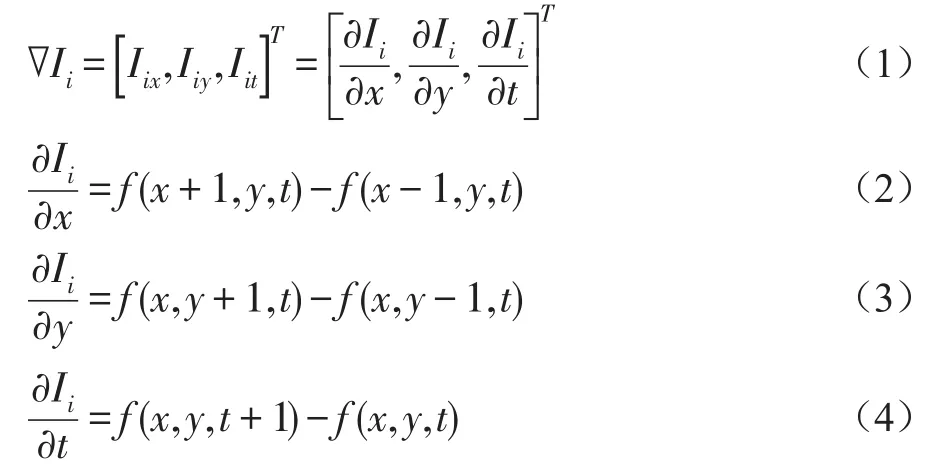
其中x,y是视频的水平和垂直方向,t表示视频的时间轴方向,f(x,y,t)表示该位置灰度图像的像素值。时空容器I中每个像素的时空梯度共同代表了该时空容器的运动模式特征。
不难看出,时空梯度特征中包含了丰富的边缘特征和运动特征。尤其适用于极其拥挤的场景,甚至可以标记出人眼都很难发现的异常事件。在其他场合,可以考虑只使用时间上的梯度来表示,这样特征向量的维度可以降低三分之二,可以大大缩短PCA运算的时间。

图3 时空容器
1.2 稀疏表示
稀疏表示在图像去噪、信号压缩等许多方面都取得了很好的效果。假设线性方程的形式为Ax=b,其中矩阵A∈Rn×m且n<m。则此方程存在无数个解,在数学上称为非欠定性问题。上述方程的解的形式为x=A-1b,用 D 表示A-1,β替代 b,则:

在这里,我们称x为原始信号,D为字典,β为x的稀疏表示。为了使解唯一,需要给方程添加一个约束条件,这里用L0范数作为约束条件,即:

这里,β∈Rm×1,‖β‖0是β的 L0范数,表示其中非零项的个数,也就是稀疏系数。字典D中每一个列向量代表一个原子,mβin ‖β‖0的意义在于用最少的原子重构信号x。如图4所示:
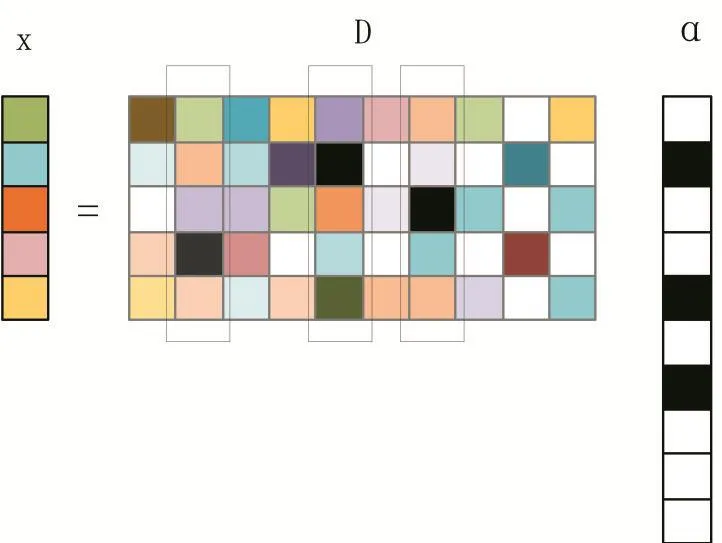
图4 稀疏表示示意图
求解字典的方法很多,由于L0范数求解方程式NP难题,所以一般用L1范数代替L0范数。求解字典的过程称为字典学习,而用字典表示新特征y的过程就是稀疏表示。设字典学习阶段得到的字典为D∈Rn×m,根据公式(7)计算出测试阶段提取的特征y的稀疏表示β:
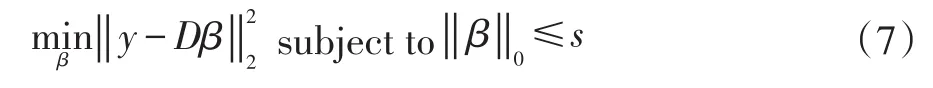
其中,β∈Rm×1,‖β‖0表示稀疏度,s为稀疏度控制 参数。是数据拟合项,同时可以将的大小与设定的阈值作比较,判断y是否属于异常事件。
求解β的过程就是从m个原子基向量中找出最多s个基向量来表示特征y,其搜索空间为,花费的搜索代价是巨大了,这也就导致了稀疏表示算法的速度很慢。
相比于稀疏表示的巨大搜索空间,稀疏组合学习的搜索空间为,其中K为预训练过程中学习到的组合个数。K个组合中的每一个组合都包含了最多s个基向量。这就大大减少了由于搜索空间大而带来的时间花费问题。稀疏组合学习的检测模型如图5所示:
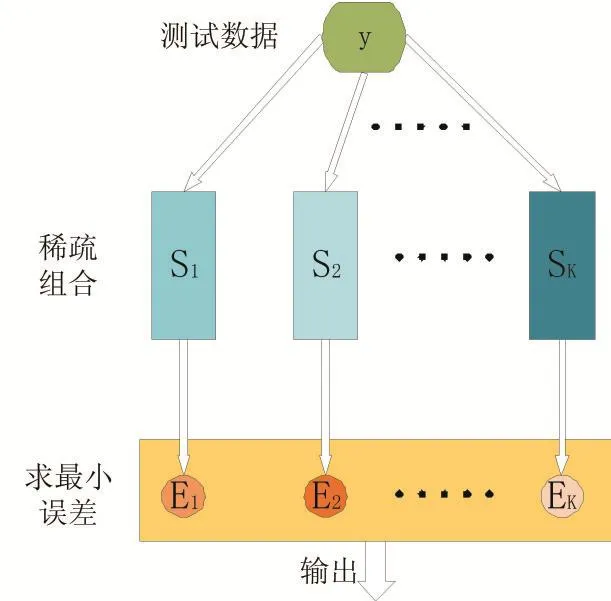
图5 稀疏组合学习检测模型
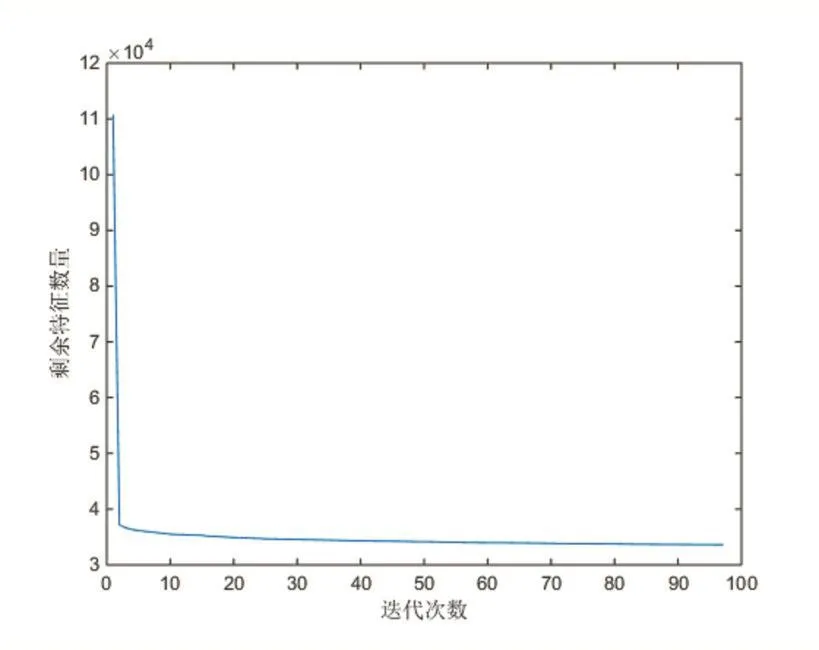
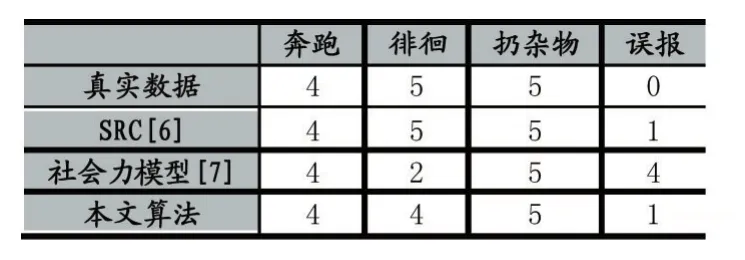
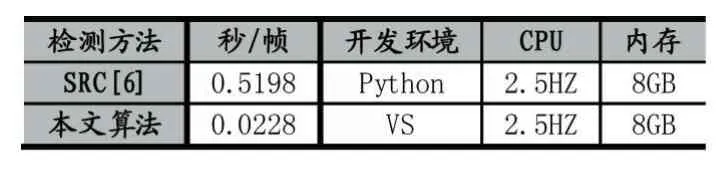
其中,y表示待测试数据,{S1,…,Sk}是学习的组合,Si∈Rn×s(s < 对于所有时空容器的三维梯度特征表示为χ={x1,…,xn}∈Rp×n,p表示单个特征的维度。训练的最终目的是找到一个稀疏组合的集合S={S1,…,SK},Si∈ Rp×s(s < 稀疏组合学习的过程就是在重构误差t下,寻找K个稀疏组合,且t和K都必须很小。所有训练数据的重构误差的和t定义为: 其中,表示xj是否选用Si进行稀疏表示。是xj对应于组合Si稀疏表示。表示只选用一个稀疏组合进行稀疏表示。 在这里,重构误差t与稀疏组合个数K就是一对矛盾的变量。t越大,那么就意味着可以用更少的组合数来表示训练数据。稀疏组合学习的目的就是在不扩大重构误差t的条件下,寻找出更少的稀疏组合。通过采用最大表示的策略可以达成这个目标。定义第j个特征的重构误差为tj,重构误差的上限为λ。则目标函数(8)变为: 稀疏组合学习是一个迭代的过程,每一次迭代就计算出一个稀疏组合。当所有的特征都能被稀疏组合表示时,训练工程就结束了。对于第i轮迭代过程,已训练出的稀疏组合为{S1,…,Si-1},不能被表示的剩余特征为χc∈χ。 计算Si时,希望其能表示χc中更多的特征。此时,目标函数(9)可变为: 其中,Ωc是χc的下标集合。在每一轮中,通过迭代更新{Si,β}和γ来达成目标函数(10)。 首先固定γ,这样(10)可变形为二次方程式: 对于所有的≠0,固定Si求最优的 β。然后,使用块坐标下降的方法获得最优的Si,反复迭代可得β的封闭解是: Si的解是: 其中,δt被设定为表示将基投射到单元列。由于块坐标下降可以收敛到全局最优,因此,L(β ,Si)可确保收敛。 更新γ。当L(β ,Si)输出后,对于每一个xj,此时的目标函数变为: 的封闭解为: 在每一轮中都会学习一个稀疏组合Si。循环学习,当剩余训练数据集合χc为空时,学习过程结束。稀疏组合学习的算法流程如下: Input: χ,current training featuresχc=χ Output: S Procedure: InitializeS=φand i=1 Loop Loop Optimize{Si,β}using(12)and(13) Optimize{γ}using(15) until Eq(11)converges AddSito S.Removeχjfrom χcifγij=0 i++ untilχc=φ return S 稀疏组合学习与子空间聚类的最大差别在于,稀疏组合学习到的组合个数是由训练数据决定的,而子空间聚类的个数则是人为设定的。由于是对正常事件建模,而且正常事件的种类数不胜数,无法预先知道训练视频中正常事件的种类,所以稀疏组合的自动聚类具有更高的准确度。 在预训练阶段学习到了K稀疏组合S={S1,…,SK},对于测试阶段提取到征x,其与每个稀疏组合的最小重构误差表示为: 它的最优解是: 则x对应于Si的重构误差为: 其中,Ip是一个P×P的单位矩阵,为了简化测试阶段中计算重构误差,为每一个Si定义一个辅助的矩阵Ri: 则对于每一个组合Si,提取的特征x的重构误差可表示为如果重构误差小于设定的阈值T,特征x就被认为是一个正常事件,否则就是异常事件。 由于真实世界中,正常事件种类繁多,随着时间的推移,离线训练的组合将不能很好地表示当前正常事件的种类,根据视频在一段时间内具有相关性,这时候就要利用当前已经检测过的正常事件,再训练出新的稀疏组合来更新当前的组合。 我们为每个稀疏组合设置一个权重w,构成一个权重矩阵。每个权重w代表了其对应的组合的活跃度。在不断的检测过程当中实时地更新权重矩阵,当权重矩阵中某个值低于设定阈值时,更新其对应组合。这样就可以使当前组合能很好地表示当前正在发生的正常事件。 在预训练出所有稀疏组合后,为每个组合设定一个初始活跃度w*,当用某个组合检测出正常事件后,增加其活跃度。为了避免某个组合的活跃度无限增大,设定一个约束条件,其中n代表了组合的总数。所以当活跃度 ωi增加 ω0后,权重矩阵ω=ω× 图6 稀疏组合学习过程中特征数量的变化 如图6所示为预训练迭代过程中,特征数量的变化,y坐标是当前训练出的组合不能表示的特征数量,可以看出在第一次迭代过程中产生的组合代表了一大部分的正常事件,所以可以认为第一组合具有很高的代表性,可以用其来更新当前组合。这样,在组合更新过程中只用进行一次稀疏组合的训练,大大加快了组合更新的速度。稀疏组合更新算法如下所示: Input:x,auxiliary matrics{R1,…,RK},Sparse combination {S1,…,SK},Weight matrixs{w1,…,wK} threshold T and w Output:abnormal event Procedure: for i=1:K do if wi end if ifthen saving x return normal event end if return abnormal event end for AVENUE数据集中,训练视频为16个只包含正常行为模式。测试视频21个,每个视频都提供有像素级别的真实标签。其中异常事件包括奔跑,错误的行走方向,异常对象,扔杂物等。 本文算法异常检测结果显示如图7-图10所示,能很好地检测出异常事件及其发生位置。 图7 奔跑 图8 抛书包 图9 扔纸 图10 自行车 从表1可以看出,SRC具有最高的精度,SRC是第一次将稀疏表示应用于异常事件检测。本文算法产生了一次误报。 表1 在AVENUE上的检测结果 但从表2可以看出SRC的处理速度非常慢,远远达不到实时性的要求。而本文算法则不一样,在兼顾准确性的同时,具有很高的处理速度,实际应用意义较大。 表2 AVENUE上处理速度比较 为了解决传统方法在人群密集场景的限制问题,本文采用了稀疏组合学习的方法。并针对其不能自适应的问题作出改进,根据当前检测出的正常特征以及稀疏组合学习迭代过程的特点再训练出一个组合,通过权重矩阵实时更新对应组合的活跃度,提高组合的自适应性。由于稀疏组合本身具备很快的检测速度,且更新过程中只进行了一次迭代运算,所以改进后的算法依然具备很高的检测速度和精度。 [1]Stauffer C,Grimson W E L.Learning Patterns of Activity Using Real-Time Tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):747-757. [2]Li Jian,Gong Shao-gang,Xiang Tao.Global Behavior Inference Using Probabilistic Latent Semantic Analysis[C]British Machine Vision Conference,Leeds,UK:BMVA,2008:1-12. [3]Y.Cong,J.Yuan,J.Liu.Sparse Reconstruction Costs for Abnormal Event Detection.In International Conference of CVPR,2011,3449-3456. [4]Lu C,Shi J,Jia J.Abnormal Event Detection at 150 FPS in MATLAB[C].IEEE International Conference on Computer Vision,Sydney,IEEE,2013:2720-2727. [5]Kratz L Nishino K.Anomaly Detection in Extremely Crowded Scenes Using Spatio-Temporal Motion Pattern Models[C].IEEE Conference on Computer Vision and Pattern Recognition,Florida,USA,IEEE,2009:1446-1453. [6]B.Antic,B.Ommer.Video Parsing for Abnormality Detection.In International Conference of ICCV,2011,2415-2422. [7]R.Mehran,A.Oyama,and M.Shah.Abnormal Crowd Behavior Detection Using Social Force Model.In International Conference of CVPR,2009.1.3 训练数据
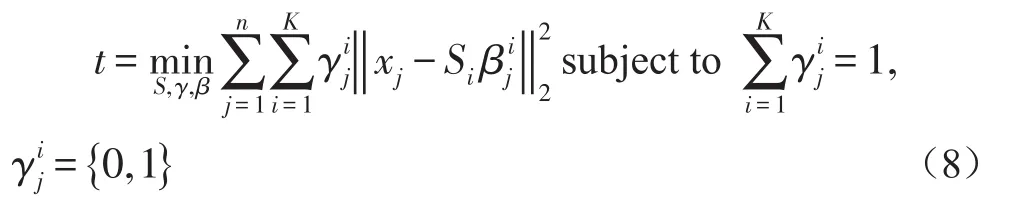
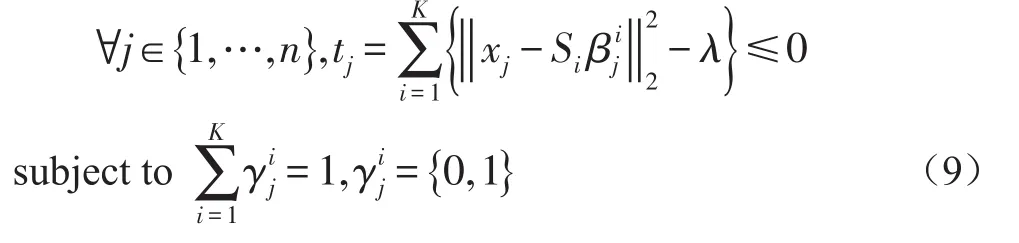
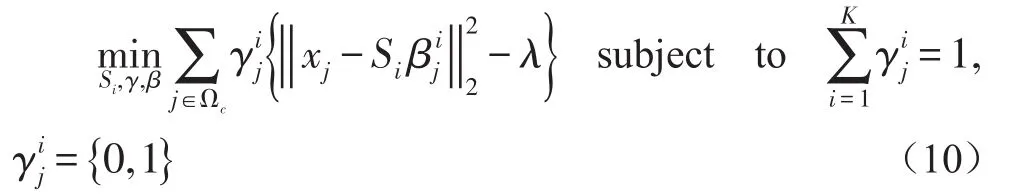
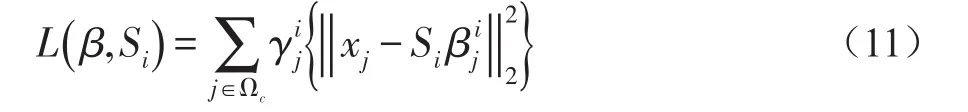

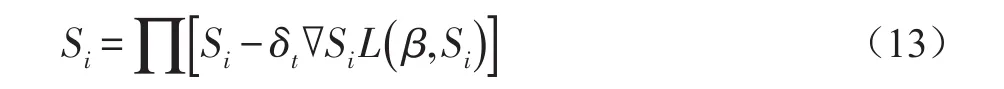
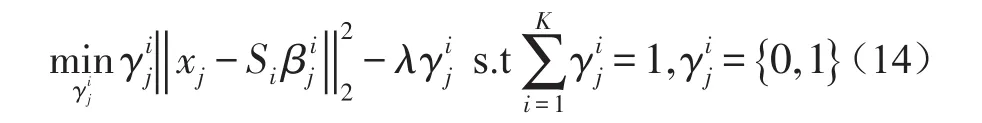
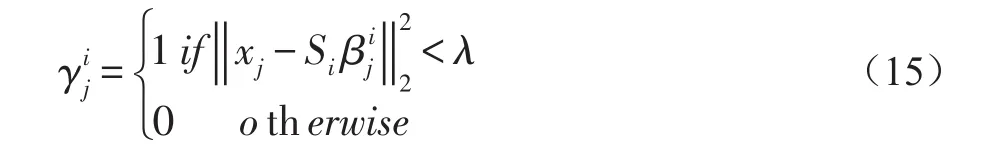
1.4 稀疏组合测试
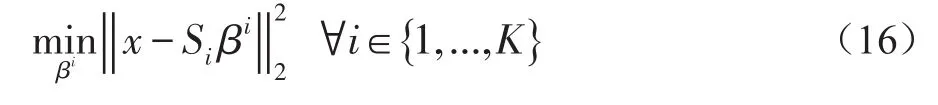

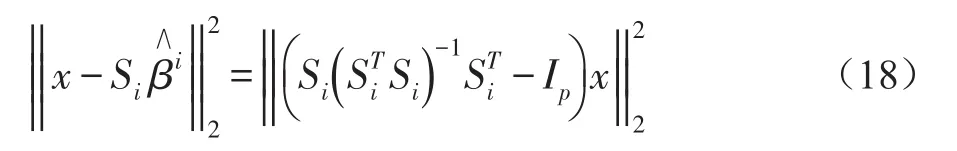
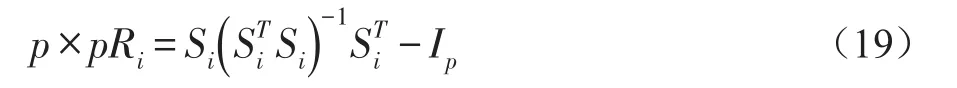
1.5 组合更新策略
2 实验结果及分析




3 结语

