基于改进极限学习机的短时交通流量预测

汤代佳,尚东方,杨露

（1.河南联合信息科技股份有限公司,许昌 461670；2.深圳大榆树科技有限公司,深圳 518033；3.上海电机学院电气学院，上海 201306）

0 引言

随着中国经济的快速发展，机动车拥有量的逐年大幅上升，在许多城市都出现了不同程度的拥堵，建立合理的交通秩序，解决交通堵塞成为大多数城市亟待解决的问题。建立智能交通系统是解决这一问题的有效途径，而实现智能交通的基础在于准确预测易拥堵路段的实时机动车流量，因为准确的交通流量预测关系到交通控制和车辆诱导的效果。针对这一问题，许多学者提出了许多有效的方法也取得了丰硕的研究成果，具有代表性的有光谱分析法、卡尔曼滤波法、神经网络预测法、小波分析方法、时间序列法等等。

这些方法采取的主要策略是提取出独特的特征信息，在一定的条件下实现流量的预测，然而由于城市道路的短时车流量具有时变性、非线性等特点，且影响车流量的各个因素无法用准备的数学公式刻画，导致传统的方法准确度不够。随着极限学习机方法的兴起，许多学者将其应用到短时交通流量的预测上，取得了不错的效果。该方法的优点在于不需要精确的数学表达式，只需利用以往同一时段观测到的信息，设置权重和层数构造神经网络，从训练过程中通过学习来抽取和逼近隐含的输入输出非线性关系，利用这一关系可以实现交通流量及交通参数的预测。

本文在已有研究成果的基础上提出了一种基于自适应混沌粒子群（Adaptive Chaos Particle Swarm Optimi⁃zation，ACPSO）算法优化的ELM算法，先用ACPSO算法优化ELM的隐层参数，然后，通过MP广义逆求出ELM的输出权值；最后，将该算法应用到短时交通流量的预测上。仿真实验表明，ACPSO优化的ELM算法具有较好的稳定性和较高的预测精度。

1 传统的极限学习机算法原理

ELM由单隐层前馈神经网络发展而来，是在MP广义逆矩阵理论的基础上提出的一种单隐层前馈神经网络的监督学习算法[16]。该算法在给定网络的输入权值和隐层偏置赋值的前提下，即可完成系统逼近，从而将神经网络训练问题转化为常规的最小二乘问题。

给定一个有N个不同样本的矩阵(xi,ti)，其中为网络输入向量∈Rm为目标输出向量，i=1,2,…,N。含有L个单隐层节点数目，L≤N,g(x)一般为Sigmoid类型的激活函数，则ELM的数学模型为：

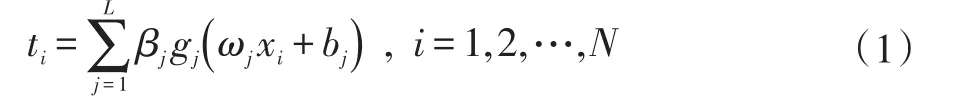
式中，βj=[βj1,βj2,…,βjm]T表示第 j个隐藏节点到输出层的连接权值；ωj=[ωj1,ωj2,…,ωjN]T表示输入层与第 j个隐层神经元的权值向量；bj表示第 j个隐层节点的偏置。式（1）可用矩阵表示为：

式中，H为神经网络的隐层输出矩阵；β为权重输出；T为输出向量。

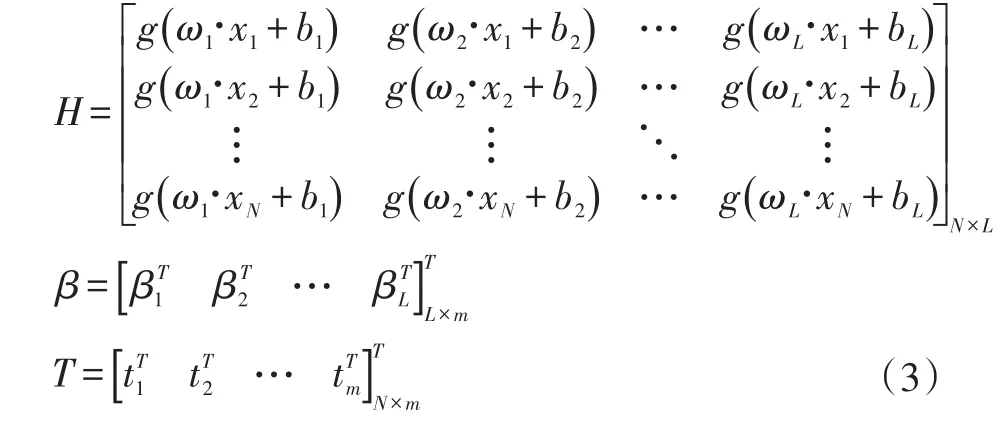
训练单隐层前馈神经网络可以转化为求解一个线性系统Hβ=T，且：

式中，H†为矩阵H的MP广义逆矩阵。由此可知，ELM算法不需要选取输入权值和隐层偏置，也不会出现局部最优解的问题。

2 基于ACPSO的改进极限学习机算法

针对ELM网络结构不稳定性，本文提出了一种改进的ELM算法。对随机生成M组输入权值ω和隐层偏置b利用ACPSO算法进行寻优，将最优的ω和b作为ELM的输入权值ω和隐层偏置b，从而增强网络的稳定性和算法的精度。

随机产生M组输入权值ω和隐层偏置b，将每组ω，b作为粒子群中一个粒子的位置矢量，即xtd=[ ]ω,b(t=1,2,…,M ，d=1,2,…,D，D为 ω和 b的维度之和)。利用迭代方式，使每个粒子向自身找到的最好位置和群体中最好粒子靠近，从而搜索到ω，b的最优解。在每次迭代中，粒子根据以下公式更新速度和位置[17]：

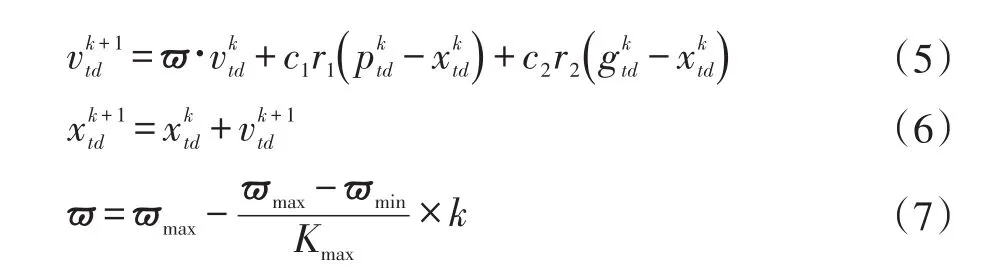
其中：vtd=[ ]vt1,vt2,…,vtD为粒子t的飞行速度，即粒子移动的距离，取值范围为[ ]vmin,d,vmax,d；c1和 c2表示学习因子，一般取2；r1和r2是区间[0,1]之间的随机数；位置xtd的取值范围为[ ]xmin,d,xmax,d；ptd表示粒子迄今为止搜索到的最优位置；gtd表示整个粒子群迄今为止搜索到的最优位置；ϖ表示惯性权重，ϖmax和ϖmin分别表示权值最大值和权值最小值；k为当前迭代次数，Kmax为最大迭代次数。

在PSO算法中，每个粒子均代表一个具有一定速度的点，每个粒子均用其各自对应的个体适应度来判断解的优劣。本文采用仿真结果出错率ft作为网络训练的适应度值，ft越小则粒子搜索性能越好。

式中，err为仿真结果出错的个数；Q为测试样本总数。由于初始化粒子是随机生成的，在迭代过程中，当粒子位置、个体极值和群体极值3个接近时，速度更新由ϖ∙vtd决定。由于ϖ<1，粒子速度越来越慢，接近于零，失去全局搜索能力，最后导致陷入局部极小。引入混沌搜索理论，利用混沌变量的随机性、规律性、遍历性能有效避免粒子在寻优过程中陷入局部收敛。对最优粒子位置变量加入混沌变量pc[18-19]，则：

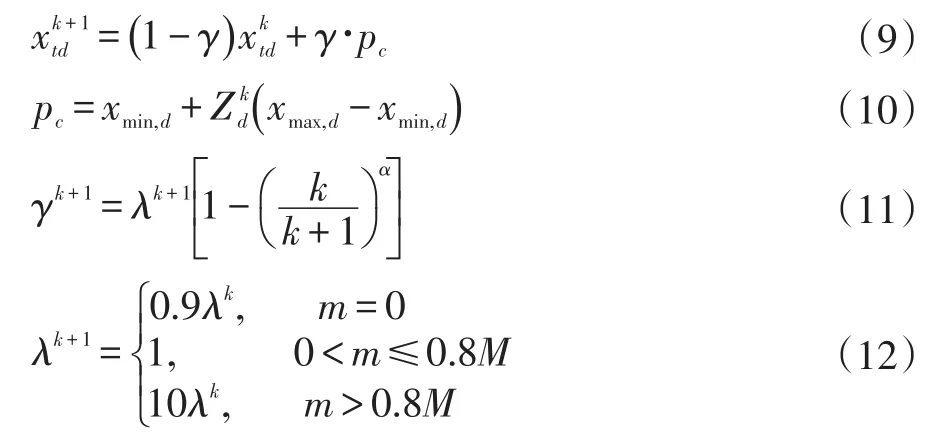
其中：pc为混沌变量经归一化处理后的混沌变量；γ为自适应权重；α为给定常数；m为通过混沌搜索算法当前迭代运算中位置更新的粒子数；M为粒子群中粒子总数；为混沌变量，一般由Logistic映射产生：

其中：μ为控制参数，μ∈(2 ,4]，初值zd在各维度上的取值范围为[0 ,1]。当 μ=4时，Logistic映射处于混沌态，可产生非周期、不收敛的混沌变量。

3 改进ELM算法在短时流量预测上的应用

3.1 数据源

每周一采集交通流量数据，共5天，具体为每天在早上6点至晚上10点，每隔20分钟记录一次路段内的交通流量数据，然后用前4次的192组数据训练神经网络，用最后一天的48组测量数据来验证交通流量预测方法的准确程度。

3.2 短时交通流量预测仿真分析

根据第2节提出的改进ELM算法，我们利用前4天的数据训练网络，得到第5天各个时段的流量预测值，将该预测值与真实值相比较，仿真曲线如图1所示。

从图中可以看出，交通的两个峰值分别出现在第6个观测时间段和第34个观测时间段，正好对应上下班的高峰时间。从预测效果看，我们所提的改进算法能较好地完成预测任务，整体来看，与真实流量相比，每个时间段的预测值均略高于实际值。

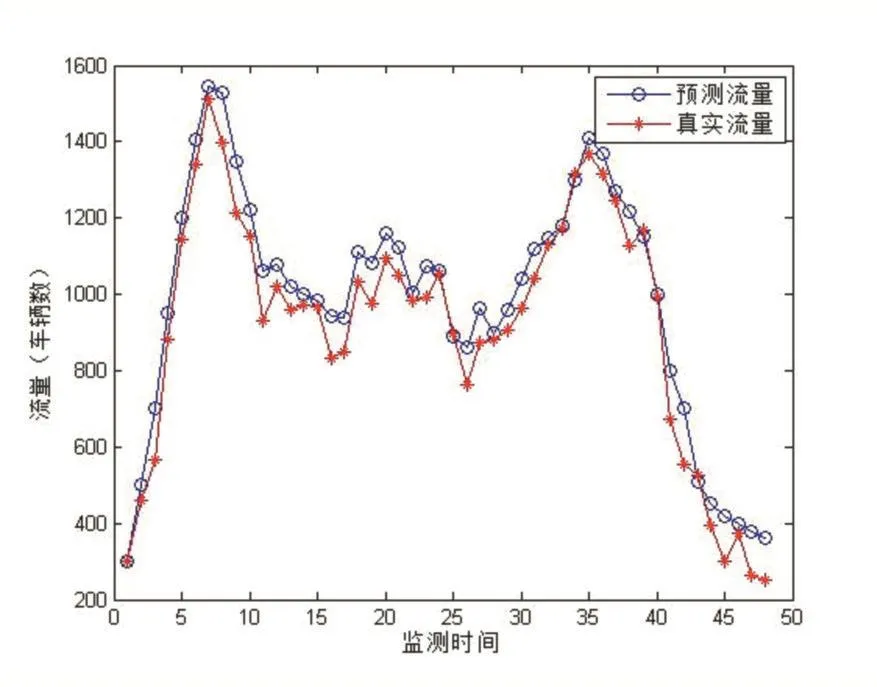
图1 短时车流量预测值及真实值

4 结语

针对传统的ELM算法预测精度低、网络结构不稳定等情况，本文提出了一种改进的ACPSO-ELM算法，通过ACPSO算法对ELM网络的隐层参数进行优化，以提高预测精度、增强网络结构的稳定性。将该方法应用到短时交通流量的预测上，仿真表明本文提出的ACPSO-ELM算法具有较好的预测精度。

[1]张敬磊,王晓原.基于非线性交通组合模型的交通流预测方法[J].计算机工程2010,36(5):202-204.

[2]HUANG Guang-bin,ZHOU Hong-ming,DING Xiao-jian,et al.Extreme Learning Machine for Regression and Multiclass Classification[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B,2012,42(2):513-529.

[3]曹琛荔,孙旋.基于神经网络与遗传算法的交通流量预测研究[J].仪表技术,2011,1:22-24.

[4]芮兰兰,李钦铭.基于组合模型的短时交通流量预测算法[J].电子与信息学报.2016 38(5):1227-1233.

[5]沈永增.基于混沌粒子群优化小波神经网络的短时交通流量预测[J].计算机应用与软件2014,31(6):84-87.

[6]HUANG Guang-bin,ZHU Qin-yu,SIEW C K.Extreme Learning Machine:Theory and Applications[J].Neurocomputing,2006,70(1/3):489-501.

[7]朱征宇.一种结合SVM与卡尔曼滤波的短时交通流预测模型[J].计算机科学,2013,40(10):248-251.

[8]李作仁,王佳玉,安雨桐,等.极限学习机在图像分割中的应用[J].电脑知识与技术,2016,03:207-209.

[9]Tchrakian TT,Basu B and Mahony M.Real-time Traffic Flow Forecasting Using Spectral Analysis[J].IEEE Transactions on Intelligent Transportation Systems,2012,13(2):519-526.

[10]毛文涛,田杨阳,王金婉,等.面向贯序不均衡分类的粒度极限学习机[J].控制与决策,2016,31(12):2148-2154.

[11]HUANG Guang-bin,ZHU Qin-yu,SIEW C K.Extreme Learning Machine:A New Learning Scheme of Feedforward Neural Networks[C].2004 International Joint Conference on Neural Networks.Budapest,Hungary:IEEE,2004:985-990.

[12]SHI Yu-hui,EBERHART R.A Modified Particle Swarm Optimizer[C].Proceedings of IEEE International Conference on Evolutionary Computation.Anchorage:IEEE,1998:69-73.

[13]LIU Hong-wu.An Adaptive Chaos Particle Swarm Optimization[C].ISECS International Colloquium on Computing,Communication,Control,and Management.Sanya,China:IEEE,2009:254-257.