基于高斯函数加权的自适应KNN算法

李昂

（上海海事大学，上海 201306）

0 引言

K近邻（K-Nearest Neighbor，KNN）算法由 Cover和Hart在1967年首次提出[1]。作为最古老的、最简单的模式识别算法之一，KNN算法在信息检索、机器学习和自然语言处理领域都有广泛的应用[2]。传统KNN算法的主要思想是：在对一个样本点进行分类处理时，首先找到与给样本点最相似的k个邻居样本点，统计分析这k个样本点的类别标签，将出现次数最多的类别标签作为待分类样本点的类别。同时，考虑到不同的邻居样本点距离待分类样本点的相似程度，为每一个邻居样本点分配各自的权重，以调节其对分类结果的影响程度。一般地，采用欧氏距离来量化两个样本点之间的相似程度。距离越远表示相似度越小，所占权重越小，反之，距离越小表明相似度越大，所占权重越大。

传统KNN算法的思路简单直观、易于快速实现。但是其通常为每一个待分类的样本点分配一个相同的k值，这种做法只在样本点在各个类别间均匀分布时才有较显著的分类效果。在实际应用环境中经常出现分布不均匀的数据集，样本点往往集中于某一个或者某几个类别中，传统的KNN算法在这种情况下往往会失去优势[3]-[5]。由此可见，k值的选取是KNN算法能否正确分类的一个关键。对于不同的样本点，根据其自身数据特点自适应地选取k值是本文的研究重点。

为了提升传统KNN算法在不平衡数据集分类中的准确度，最优k值的选取一直以来被广泛关注，大部分的理论工作集中于为每一个待分类的数据集找到最优的k值，但是忽略了数据集的具体结构和需要分类的样本点的基本属性[6]。例如，Samworth针对KNN算法提出了最优权重向量的最优表达式，同时可以求出数据集的最优邻居数[7]。但是这个结果只在数据集中化的样本点趋于无穷大是才能够成立；对于基于内核的方法，也存在几种适应性地选择内核带宽（等价于k值）方案[8-11]。但是在实际应用中，对内核函数的选择没有原则性的方法。此外，上述对于权重以及k值的选取在给定数据集下，对于所有的待分类样本点都是相同的，并没有针对具体数据集内样本点的具体分布情况，为每一个样本点分配最优的k值[12-14]。2010年Sun等人针对该问题提出了一种自适应的k值选取方法，选用距离最近邻居样本点的k值作为自己的最优邻居数[3]。这种方案思路简单易于实现，并且可以做到自适应的为每个样本点选取k值，但是由于方案没有充分考虑到样本点分布不平衡的问题，导致分类结果会出现一定的误差。2017年，Anava等人提出了一种自适应的KNN算法，可以为每个样本点自适应的计算权重向量和k值，但是该算法在同时计算出权重向量和k值的同时需要消耗大量的计算资源[6]。

本文在Sun等人的基础上，对自适应的KNN算法进行了改进，充分考虑到数据集内样本点的具体分布和计算资源的消耗，提出了一种轻量级的自适应k值计算方案。并且通过实验验证了该算法的分类准确率和计算效率。实验表明轻量级的自适应KNN算法在准确率和计算效率方面较以往算法有一定的提高。

1 预备知识

1.1 系统建模

将一个分类算法抽象为系统参数(k,w,ω)、类别标签集Y、样本分类函数Y、距离函数d、样本判别函数c、训练样本集 Xtrain、待分类样本集 Xclassify。其定义如下：

●系统参数(k,w,ω)中k表示某一个样本点X的最近邻个数；分量权重向量w=(w1,w2,…,wn)分别表示在计算距离时，样本点向量X每一个维度的权重值；距离权重向量 ω=(ω1,ω2,…,ωn)表示某一样本点 X 的最近邻集合中每个样本点的权重。

●用一个n维向量X=(x1,x2,…,xn)表示一个样本点，它是KNN分类算法的基本单位。对于某一个样本点Xi来说，kNNXi={X1,X2,…,Xk}表示的是与Xi最近的k个邻居样本点的集合。

●类别标签集Y={y1,y2,…,ym}是系统中的所有类别标签的集合，yi是其中第i个标签的标号。

●样本分类函数Y:Rn→R用来给出某一样本点的类别标签。对于一个待分类的样本点Xi，其分类结果可以表示为：

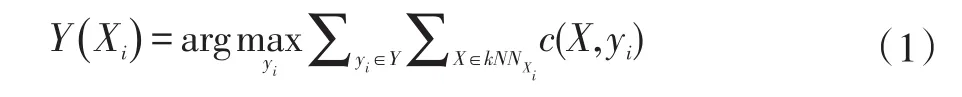
若Y(X)=yi表示样本点X对应的类别标签为yi；特别地，若某样本X的类别标签未被确定，则Y(X)=⊥。

●距离函数d:Rn×Rn→R用于计算两个样本点之间的距离，一般地，取欧氏距离d(Xi,Xj)=作为两个样本点之间的距离测度。其中Xi,Xj是两个不同的样本点，wr是样本点向量第r维的权重。

●样本判别函数c:Rn×N→{0,1}用于判断样本点是否属于某一类别，若c(X ,yi)=1表示样本点X属于类别 yi，若 c(X ,yi)=0则表示样本点X不属于类别yi，其中i=1,2,…,m。

●训练样本集Xtrain={X|Y(X )≠⊥}是一个类别标签已知的样本点集合。

●待测样本集Xclassify={X|Y()X=⊥}是一个类别标签未知的样本点集合。

1.2 传统的KNN算法

由于具有简单直观的特点，因此传统KNN算法是目前应用最广泛的模式识别算法之一。对于一个特定的数据集，通过交叉验证的方法为整个系统中的每一样本点设置统一的k值。一个标准的KNN分类算法的步骤如下：

（1）输入包含M个样本点的训练样本集Xtrain，通过交叉验证法确定系统参数k；

（2）输入包含N个样本点待测样本集Xclassify，对于Xclassify每一个样本点X，运用距离函数d计算其与训练样本集Xtrain每一个样本点的距离矩阵其中，dij表示第i个待测样本与第 j个训练样本的欧氏距离。

（3）依 次 遍 历 距 离 矩 阵DN×M的 行 向 量(di1,di2,…,diM)并根据大小进行排序，选择距离最小的k个距离记录其下标。

（4）对于一个每待测样本点Xi，根据（3）中记录的最近邻下标，取其最近的k个训练样本点，构成Xi的最近邻集合kNNXi⊂Xtrain。

（5）根据式（1）对样本点Xi的分类进行预测，记录分类结果Y(Xi)；重复（4）和（5）直至所有样本分类完毕。

（6）统计分类结果并分析正确率。

这种为所有的样本点设置固定的k值的做法的前提是所有的待测样本点均匀分布在各个类别的数据集中。在样本点分布不平衡的数据集中，不同类别之间样本点的个数差别较大。这在种情况下，如果为每一个待测样本点都分配相同的k值，很可能要大于该类别内的样本点总数，分类结果会受到严重的偏差。因此，根据每个待测样本点的分布特点为其分布合适的k值可以大大提高KNN算法的准确度。

2 基于高斯函数加权的自适应KNN算法

为了适应不平衡的数据集，需要根据样本点在样本空间中的分布情况为每一个样本点自适应的设置k值。基于高斯函数加权的自适应KNN算法利用高斯函数计算距离权值向量ω，并根据ω计算样本点的自适应最近邻个数k。自适应的k值计算分为两个部分，一是为训练样本集Xtrain中的每一个训练样本点计算合适的最近邻个数kj；二是根据Xtrain中各个样本点的最近邻个数ki，计算待测样本集Xclassify中样本点的最邻个数k。i

2.1 训练样本点 k值计算

在一个容量为M的训练样本集Xtrain中，为了确定某样本点的最优近邻个数kj，需要计算与其他M-1个样本点的欧氏距离为了降低计算复杂度，算法规定最近邻个数k∈[1,9]。因此只取与样本点最近的9个邻居样本点，构成最近邻集合随后根据式（2）计算邻居样本点的距离权值，得出的权值向量距离权值计算方式如下：

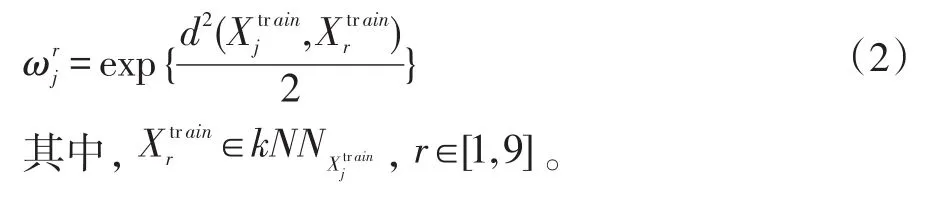
对于 kj，r∈[1,9]，根据式（3）计算最近邻个数 k的概率分布：

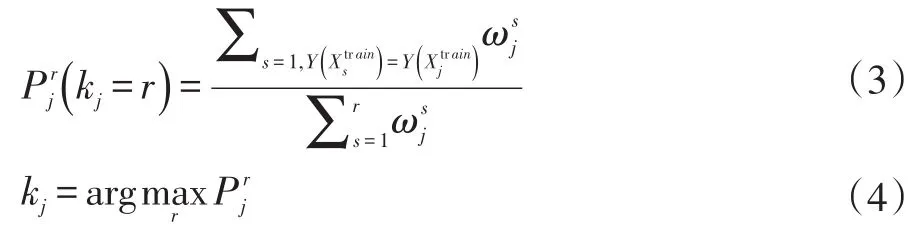
训练样本的最优邻居数kj由式（4）确定，即选择概率最大的最近邻个数。算法1给出了计算训练样本点最近邻个数的具体步骤。

2.2 待测样本点k值计算

在一个容量为N的训练样本集Xclassify中，为了确定某样本点的最优近邻个数ki，首先计算与M个训练样本点的欧氏距离同样取与样本点最近的9个邻居样本点，构成最近邻集合向量的分量表示最近邻集合对应样本点的最优近邻个数，k可由式（4）计算得出。根据式（5）计算的权值向量其中则待测样本点的最优近邻个数可以根据式（6）确定。

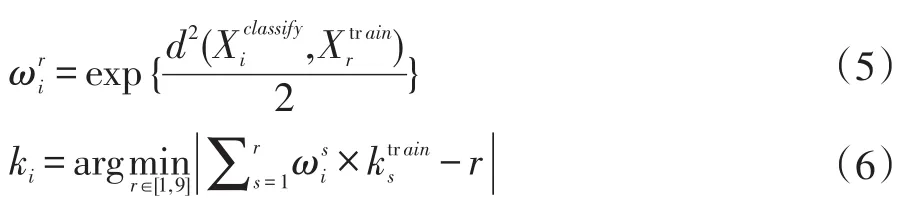
算法1计算训练样本k值

最后，根据式（1）对样本点Xi的分类进行预测，记录分类结果Y(Xi)。算法2给出了计算待分样本点最近邻个数的具体步骤。

算法2计算待测样本k值

3 实验结果

为了验证本文算法的有效性，我们设计实验，将本文算法的分类准确率与传统KNN算法[1]、典型的Nada⁃rays-Watson算法[11]比较。

3.1 实验平台与实验数据

算法的测试平台为Windows 10，测试环境为测试环境为CPU Intel Core i5-7200U 2.50GHz，内存8GB的PC，用JupyterNotebook实现。

本文选取了10组UCI数据集（https://archive.ics.uci.edu/ml/machine-learning-databases）作为验证集。对于每个数据集，随机取90%的样本作为训练集，另外10%的样本作为待测样本集。在每个数据集中，样本数据都是由数值组成。表1中前5个数据集（Iono⁃sphere，Parkinsons，Pima，Haber，Blood）为 二 元 分 类yi∈{0,1}，后5个为多元分类。表1显示了实验数据分布情况。

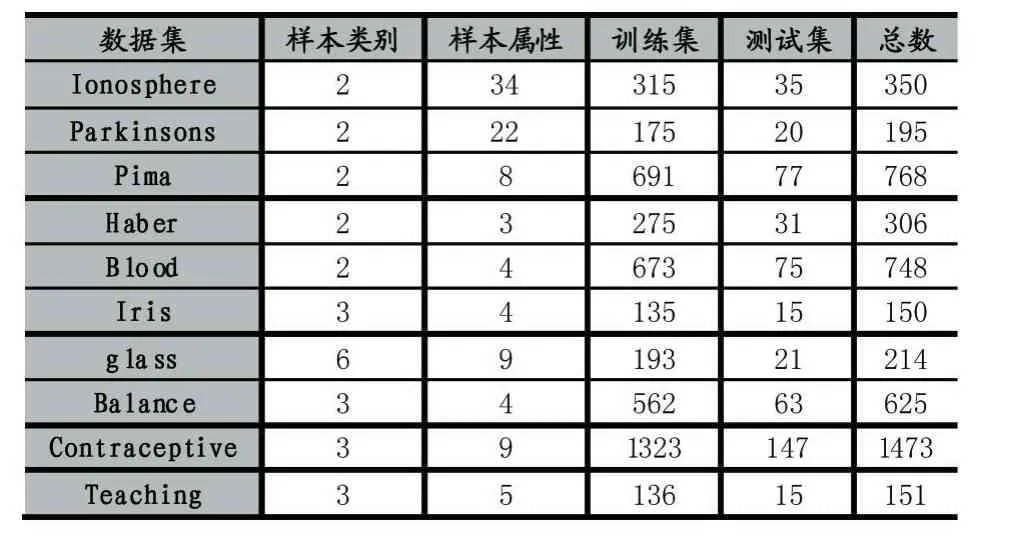
表1 实验数据分布

3.2 实验步骤

（1）选择样本：输入样本数为N的数据集，随机选择其中90%为训练集，剩下的10%为测试集。对于每个样本集，得到10个训练集与10个测试集。

（2）标准kNN算法和Nadarays-Watson算法：在（1）中得到的10个测试集上进行标准的kNN算法以及Nadarays-Watson算法。

（3）得到每个样本的最优k值：对于每个训练集运用算法1，计算得出训练集中每个样本的最优k。

（4）自适应的KNN算法：由（3）中得出的最优k，在（1）中得出的测试集中进行算法2。

（5）计算上述3种算法中10个测试集的平均准确率。

（6）比较（5）中得到的不同的结果。

3.3 实验结果

按照3.2中的步骤进行实验，所得的三类算法的准确度在表2和表3中显示。

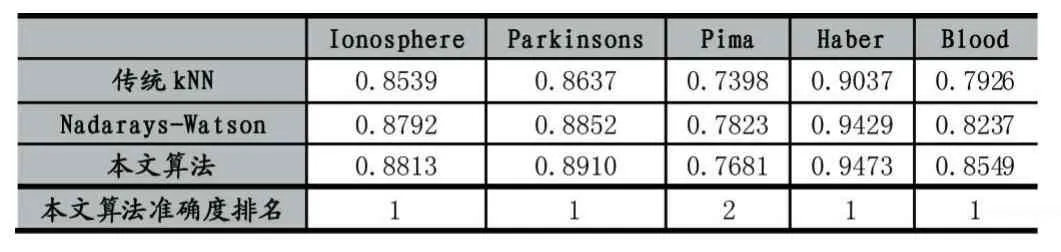
表2 算法的准确度比较（前5个数据集）

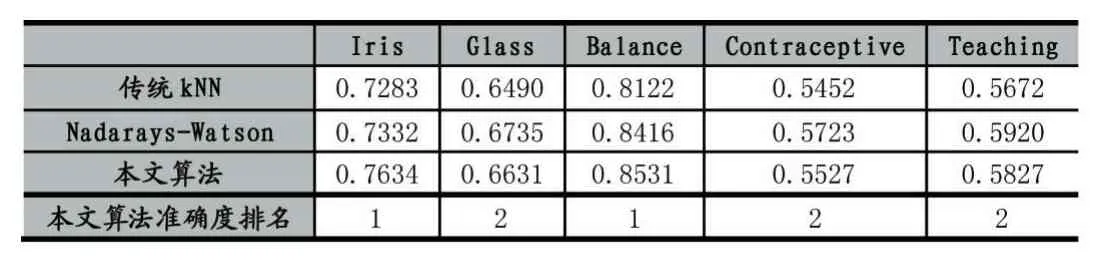
表3 算法的准确度比较（后5个数据集）

从实验结果可以看出1）本文相较于传统的KNN算法有更高的准确度，并且在其中6个数据集中准确度高于Nadarays-Watson算法。其中在数据集Haber中准确度最高，在数据集Contraceptive中准确度最低；2）对比表2和表3可以得出，与多元分类相比，KNN算法在二元分类中的准确度较高。

4 结语

本文在Sun等人的基础上，针对待分类数据分布不均的情况，提出了一种基于高斯函数加权的自适应KNN算法。该算法能过根据样本点的分布情况自适应的为每个样本点分配最近邻个数（k值）。实验结果表明，该算法相较传统的KNN算法与基于核函数的Nadarays-Watson算法在分类精度上具有明显的优势。

[1]COVER M,HART P.E.Nearest Neighbor Pattern Classification.IEEE Transactions on Information Theory,13（1）:21-27,1967.

[2]毋雪雁,王水花,张煜东.K最近邻算法理论与应用综述[J].计算机工程与应用,2017,53（21）:1-7.

[3]SUN S,HUANG R.An Adaptive K-Nearest Neighbor Algorithm[C].Seventh International Conference on Fuzzy Systems and Knowledge Discovery.IEEE,2010:91-94.

[4]王超学，潘正茂，马春森等.改进型加权KNN算法的不平衡数据集分类[J].计算机工程,2012,38（20）:160-163.

[5]GHOSH A K.On Optimum Choice of k in Nearest Neighbor Classification[J].Computational Statistics&Data Analysis,2006,50（11）:3113-3123.

[6]ANAVA O，KFIR Y.L.k*-Nearest Neighbors:From Global to Local[C].Advances in Neural Information Processing Systems.2016:1-16.

[7]SAMWORTH R.J.Optimal Weighted Nearest Neighbour Classifiers.The Annals of Statistics,2011,40（5）:2733-2763.

[8]ABRAMSON I S.On Bandwidth Variation in Kernel Estimates-A Square Root Law[J].Annals of Statistics,1982,10（4）:1217-1223.

[9]SLIVERMAN B.W.Density Estimation for Statistics and Data Analysis,Volume 26.CRC press,1986.

[10]DEMIR S,TOKTAMIS Ö.On the Adaptive Nadaraya-Watson Kernel Regression Estimators[J].Hacettepe University Bulletin of Natural Sciences&Engineering,2010,39（3）:429-437.

[11]KHULOOD H A,LUTFIAH I A T.Modification of the Adaptive Nadaraya-Watson Kernel Regression Estimator[J].Scientific Research&Essays,2014,9（22）:966-971.

[12]KULIS B.Metric Learning:A Survey[J].Foundations&Trends® in Machine Learning,2013,5（4）.

[13]BIAU G,DEVROYE L.Lectures on the Nearest Neighbor Method[M].Springer International Publishing,2015.

[14]HASTIE T,TIBSHIRANI R.Discriminant Adaptive Nearest Neighbor Classification[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,1996,18（6）:607-616.