基于排队论的东营港规划航道通过能力确定

，，，，，

(1.武汉理工大学 a.航运学院；b.内河航运技术湖北省重点实验室，武汉 430063；2.中华人民共和国东营海事处，山东 东营 257000)

伴随着进出港船舶呈现大型化发展趋势，船舶密度也日益增大，一些港口的进出港航道已经成为限制港口发展的“瓶颈”[1]。东营港作为山东省地区性重要港口，依据《东营港总体规划修订报告》(以下简称《规划》)，东营港计划将主航道扩充为10万t级单线兼顾5万t级双向通航[2]，为评估东营港规划航道与港区的匹配程度，有必要对东营港规划航道的通过能力及服务水平进行研究，以确定东营港规划航道的通过能力。

关于航道通过能力确定方面的研究，目前主要采用的是静态的方法，如利用“西德公式”“长江公式”“川江航道公式”[3]等经验公式来计算特定航道通过能力，还有的学者利用求船舶航迹带宽度、最大吃水、载重吨的方法来确定航道通过能力[4-5]，但是这些方法的公式中存在许多经验系数，主要运用于内河航道通过能力计算，运用到海港航道通过能力计算误差较大。在动态方法研究方面，有些学者运用Rockwell arena软件进行建模仿真[6]、结合离散时间系统仿真理论进行研究[7]等，而港口航道是一个随机服务过程，以上的方法不能很好地反映船舶在航道及进出港过程中的随机规律。

排队论在港口最佳锚位数确定[8]、物流运输资源最优化分配的问题[9]，配电公司的车辆配置问题[10]等领域得到广泛应用，也有学者把排队论应用到航道通过能力研究，如运用排队论法构建动态模型、仿真模型用来评价港口航道的饱和度[11]等。为了尽可能地减少误差，在前人研究的基础上，根据东营港航道规划的相关规定，选择与规划航道相匹配的标准船型作为代表船型，在确保船舶在航道中安全航行及在港口满足相关的服务水平要求的情况下，来确定东营港规划航道的通过能力。

1 模型

船舶靠泊的过程按照船舶-锚地-航道-泊位系统运作，该过程可视为港口的随机服务过程，泊位即为服务窗口，航道就是排队容器，假设锚地容量是充足的，运用排队论理论的相关知识，求出相关的参数，从而求出港口航道的通过能力。在进行港口航道通过能力的排队论建模时，需要考虑到以下因素。

1)通过对港口作业过程的分析，船舶从到达港口到货物装卸完毕离港，整个过程船舶到达规律服从泊松分布，即在时间区间(0，t](t>0)内概率密度函数Pn(t)为

(1)

式中：λ为船舶平均到港率，即单位时间内平均到港船舶数。

2)进入航道等待靠泊的船舶通常遵循先到先服务的方式。由于本文研究东营港规划航道通过能力，因此在该排队论模型中通过航道的排队船舶为单列形式，见图1。

该模型对船舶来源没有限制，因此可得到如图2所示船舶靠泊的马尔科夫状态流。

可列出相应的K氏代数方程：

(2)

为了使航道通过能力由航道本身的特点决定，同时考虑尽可能地使航道的通过能力达到最大，现假设码头存储的货物是充分的，能使船舶进出港船舶满载，还有就是泊位数量是充足的，进入航道的船舶都是有泊位为之服务的。

3)排队系统平均队长的确定，参照公式(3)。

(3)

式中：Ls为港口航道的通过能力，平均队长Ls即为航道的通过能力；Lq为等待服务船舶数；ρ为服务强度；P0为系统中没有船舶的概率；n为服务台数量。

2 计算东营港规划航道的通过能力

2.1 东营港规划航道介绍

东营港区航道规划先形成一个完整的防护水域基础，规划进港航道建设双防波潜堤。航道方位与现有栈桥平行，航道方位为235°～55°，航道按10万t级单线兼顾5万t级双向通航考虑，航道通航宽度为357 m，设计底高程为-17.0 m，长度为15.3 km。见图3。

2.2 港口航道通过能力的排队论模型参数的确定

要计算东营港规划航道的通过能力，应包含进港排队论系统、出港排队论系统两个过程。与进港排队论系统相比，出港排队论系统的服务时间不包括在码头泊位装卸货的时间。

2.2.1 东营港码头作业天数

风、流等气象条件会影响码头泊位的正常使用,如果不把这个因素考虑进去，模型计算误差就会很大。采取的办法是根据港口的气象统计信息，排除1年内码头不能使用的天数，将统计时间内到港的船舶按照前面得到的码头泊位实际作业天数平均分配,通过用这种方法计算平均到达率就可以减小模型的误差。

码头船舶作业主要受降水、风、雾、波浪和海冰的影响，根据东营海事局的相关规定，船舶允许装卸作业标准如下[12]。

风：≤7级；雨：≤中雨；雾：能见度≥1 km。

波浪：集装箱船和杂货船横浪H4%≤0.8 m、顺浪H4%≤1.0 m。

海流：顺流流速≤1.25 m/s。

冰：密集度<8级,浮冰量<8级,冰厚<15 cm。

根据东营海域自然环境概况的分析，可以大体得到东营港码头的作业天数，见表1。

表1 自然因素影响作业天数表

综合分析,影响作业天数取为35 d,即年作业天数为330 d。

2.2.2 代表船型的选择

为确定东营港规划航道的通过能力，首先应选取准确的代表船型。代表船型的选择遵循以下原则：①尽可能地选择与东营港规划航道建设标准相匹配的标准船型；②选择的标准船型能够使东营港规划航道的通过能力达到最大。

东营港规划航道设计代表船型见表2。

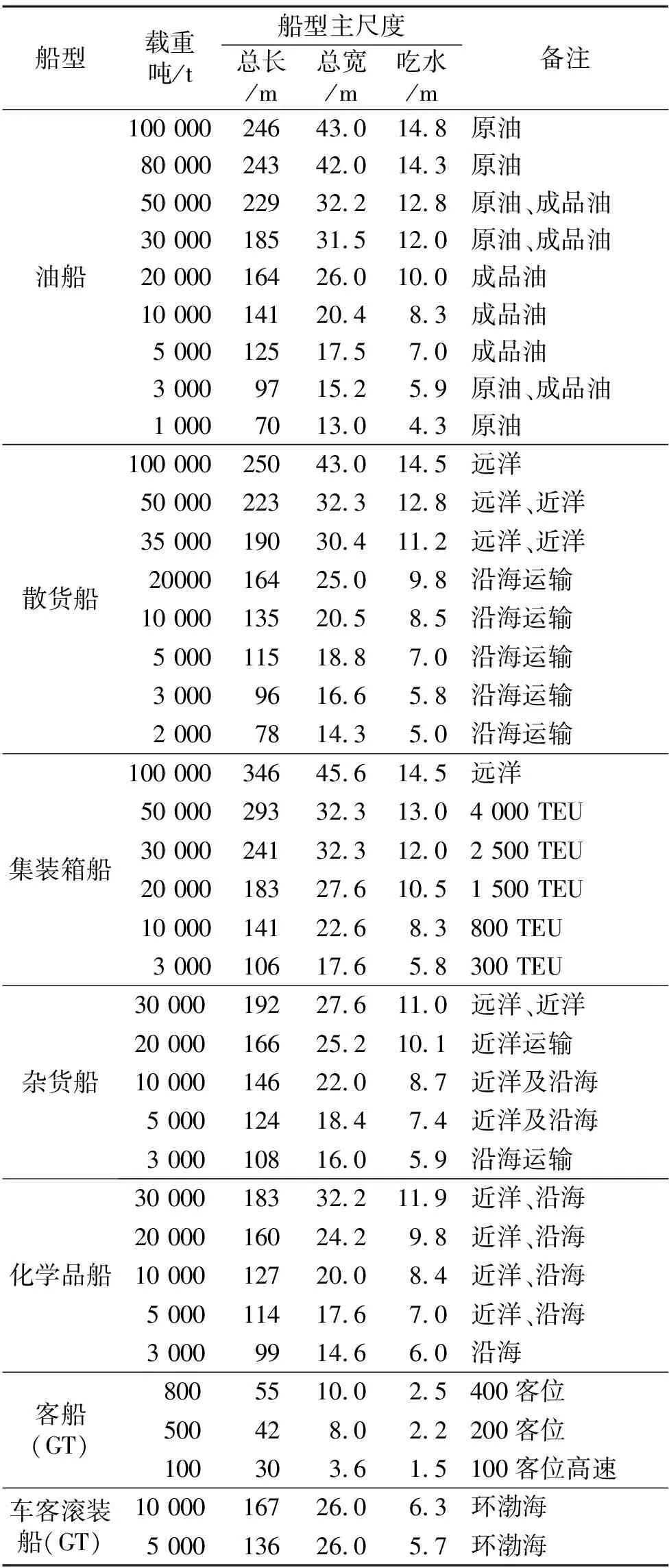
表2 东营港规划航道设计代表船型统计表

东营港规划航道代表船型选择的标准如下。

1)航行规则：单向全天候通航>单向乘潮。

2)因大型船舶更能发挥航道效率，因此同等条件下，选择大型船舶为代表船型[13]。

3)根据东营港区总体规划的调整、运量预测及到港船型预测分析，同等条件下选择油船为代表船型。

根据表3，单向航行中8万t级及以下油船通过规划航道是不需要乘潮的，综合考虑以上的标准，选取8万t级的油船为东营港规划航道通航能力确定的代表船型，航行规则选择单向全天候通航。代表船船型尺度见表4。

2.2.3 服务台数n的确定

根据港口航道通过能力的排队论模型，服务台n为在码头泊位与航道容量中取最小值，东营港规划生产性泊位157个，航道容量的确定方法如下。

根据日本著名学者藤井提出的船舶领域的理论，港口航道属于船舶航行需要减速通过港口内部的情况。此时船舶领域的尺度为长轴6倍船长，短轴为1.6倍船长的椭圆型区域[14]。见图4。

可以得到航道交通容量公式为

(4)

式中：Np为航道容量，艘/d；v为平均航速，m/h；W为航道宽度，m；ρmax为最大船舶密度，艘/m2；r、s分别为船舶领域长半径和短半径。

按照2011年东营港总体规划，东营港规划航道宽度357 m，长度15.3 km，取进出港平均航速为9 kn,即v=1.67×104m/h，r=1 458 m，s=388.8 m,得到航道容量Np=10.5 艘/d。

综上所述，进出港排队系统的服务台n为10.5。

表3 航道设计底高程计算表

表4 代表船船型主尺度表

2.2.4λ、μ的确定

1)船舶平均到达率λ。依据吞吐量预测和货物流量分析，预计2020年东营港区规划航道年到港船舶数为2 723艘。

泊位的平均到达率λ为

(5)

式中：N为港口泊位平均作业天数，此处取330 d；M为进出港船舶艘数，艘。

因此λ进=λ出=8.25艘。

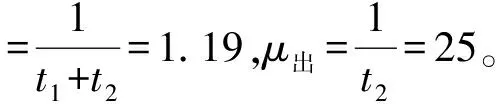
2.2.5 港口服务水平评价指标

AWT/AST值为航道服务水平的评价指标，根据《发展中国家港口规划手册》中提到的相关建议，我国港口AWT/AST值适合取0.5以下。AWT为船舶平均等待时间，即为平均等待航道时间与平均等待泊位时间的和；AST为平均在泊停靠时间，包括船舶在泊位装卸作业时间和装卸完毕后等待出航道的时间[15]。AWT、AST的计算如下。

AWT=Wq，AST=Ws-Wq

(6)

式中：Wq为等待时间；Ws为逗留时间。

根据模型中计算公式计算得到：

1)进港排队论系统。见表5。

表5 进港排队论系统服务水平评价指标参数表

2)出港排队论系统。见表6。

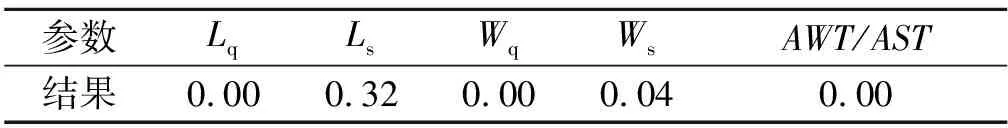
表6 进港排队论系统服务水平评价指标参数表

2.3 结果分析

表7 东营港规划航道通过能力计算表

根据上表，本模型计算得到东营港规划航道的通过能力为9.94 艘/d，由作业天数为330 d，得到东营港规划航道全年可通过的最大货运量为2.624亿t，航道服务水平的评价指标：AWT/AST= 0.39<0.5。根据《规划》，预测东营港规划航道的通过能力为3亿t，与本文计算结果接近，同时《规划》中给出了2020年、2030年、2040年东营港由规划航道承担的货物总吞吐量将分别达到0.8亿t、1.5亿t和1.9亿t，东营港规划航道是能够满足未来港区发展需求的。

3 结论

1)根据基于排队论的航道通过能力计算模型计算得到的东营港规划航道的通过能力为9.94艘/d，全年可通过的最大货运量为2.624亿t，满足东营港远期规划的需求，计算结果与规划预测结果接近，验证了该模型可信度与有效性。

2)将排队论运用到港口航道通过能力计算中，考虑到了静态模型中忽略船舶到港及装卸服务的随机性与统计规律；根据东营港的实际情况提出了代表船型的选择标准，用可通过的代表船型的数量及货运量作为航道的通过能力；考虑到船舶在航道中航行的安全，应用藤井的船舶领域模型来保证船舶在保证安全航行的前提下计算航道的通过能力等。

3)本模型把尽可能多的因素考虑进去，但航道通过能力公式计算过程较为麻烦，调研的资料可能存在误差等，有待在后续的研究工作中进一步完善和改进。

4)在《规划》中，航道通过能力是采用静态经验公式进行计算的，本文计算结果可以为东营港港区规划建设提供参考，对东营港规划航道与港区的匹配程度进行评估，避免规划航道的建设不能满足远期港区建设的需求。该模型也可以为其他港口航道通过能力的确定提供借鉴。

[1] 黄泰坤,王元战,李绍武,等.海港复式航道通过能力动态系统仿真[J].大连海事大学学报,2015(1):20-26.

[2] 中交第一航务工程勘察设计院.东营港总体规划修订报告[R].东营：东营市人民政府，2016(11).

[3] 刘敬贤,韩晓宝,易湘平.基于排队论的受限航道通过能力计算[J].中国航海，2008(3)：261-264，268.

[4] 淦学甄,艾万政.桥区航道通过能力分析[J].船海工程,2015(3):132-134.

[5] 饶思梁.内河航道尺度与通航能力关系研究[D].武汉：武汉理工大学,2015.

[6] 周伟,吴善刚,肖英杰,等.基于Arena软件的LNG船舶通航组织仿真[J].上海海事大学学报,2014(2):6-10.

[7] 孟宁,陈燕,王军.多浅段航道设计通过能力仿真[J].大连海事大学学报,2011(1):63-67.

[8] 贾松松.基于排队论的港口最佳锚位数研究[D].大连：大连海事大学,2011.

[9] BRANDAO J. A deterministic tabu search algorithm for the fleet size and mix vehicle Routing Problem[J]. European Journal of Operational Research,2009，195(3)：716-728.

[10] Aleksandar Janjic. Two-step algorithm for the optimization of vehicle fleet in electricity distribution company[J]. Electrical power and energy systems,2015,65(2)：307-315.

[11] 曹兴飞.基于排队论的港口航道通过能力仿真研究[D].大连海事大学,2015.

[12] 赵红红.东营港通航安全评估研究[D].青岛：中国海洋大学，2012.

[13] 卞艺杰.内河航运中的船舶流当量研究[J].河海大学学报(自然科学版),2000(6):97-99.

[14] 刘绍满,王宁,吴兆麟.船舶领域研究综述[J].大连海事大学学报,2011(1):51-54.