基于多步新息的机动检测方法
王 勇
(江苏自动化研究所,江苏 连云港 222061)
0 引言
机动目标跟踪主要包括观测数据预处理、机动目标模型、机动检测与机动辨识、滤波与预测以及跟踪坐标系和滤波状态变量(即目标空间位置定位与描述)的选取等。其困难主要来源于两个方面:一是目标运动的不确定,二是观测数据的噪声。要解决此困难,一个重要的环节就是机动检测[1-3]。
机动检测的主要思想是根据观测量Y(k)与状态预测量()构成的新息向量 d(k)=Y(k)-的变化情况,按照某一准则或者逻辑进行机动检验。基于机动检测结果,自适应调整系统状态噪声阵或滤波增益,对机动目标的运动状态进行滤波估计和预测,从而实现对机动目标的跟踪功能。因此,可靠及时地检测出目标机动模式直接影响机动目标跟踪的性能。
进入21世纪后,由于电子技术的快速发展,反舰导弹性能有了大幅度提高。末端防御系统为了提高对反舰导弹的处理能力,一种方法是提高火控系统数据率,以充分使用跟踪器的目标量测数据,提高对超音速反舰导弹的解算处理能力。针对系统数据率提高,传统的基于新息的机动检测方法[4-7]不再适用。为此,本文提出了一种基于多步新息的机动检测方法,可较好地提取出目标机动信息,便于机动检测,并通过仿真计算,对于给定虚警率,针对基于衰减记忆的机动检测方法,给出最小机动检测延迟与衰减系数的关系。
1 多步新息计算方法
目标动态模型用来描述目标状态X关于时间的变化情况。常用的是状态空间线性模型(连续时间模型)为:
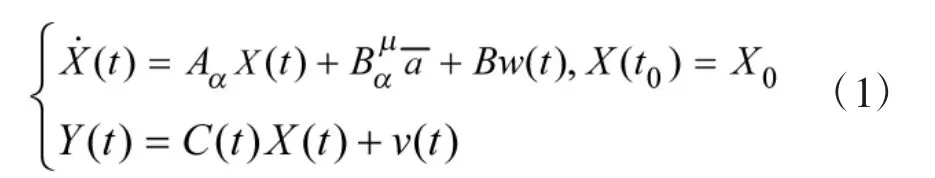
或离散时间模型为:
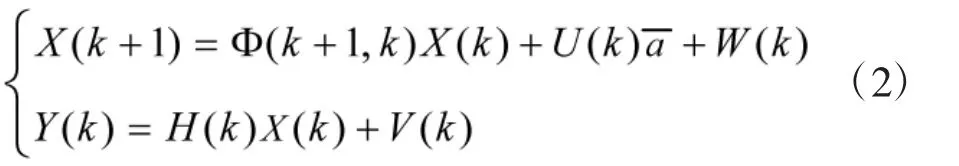
以离散状态方程为例,X(k)、Y(k)和 U(k)分别是目标状态、观测和控制输入在k时刻的向量;Φ(k+1,k)和H(k)分别是适当维的系统状态转移矩阵和观测矩阵;W(k)和V(k)分别是系统模型噪声和观测噪声,且噪声W(k)和V(k)为互不相关的高斯白噪声序列,其统计特性为:
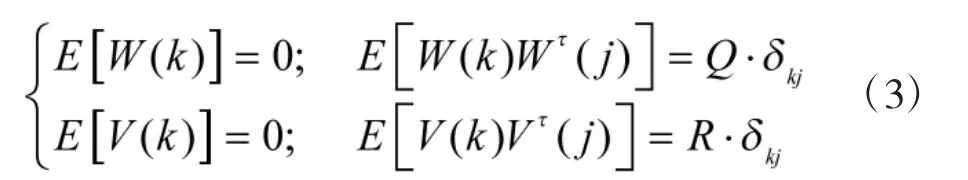
其中,Q、R分别为系统噪声和观测噪声协方差矩阵[8-9]。
新息为观测量与预测之间的差值,其公式表示为:
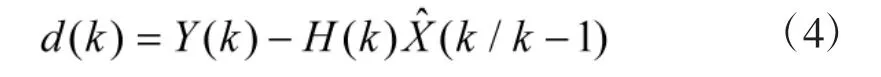
文献[4]证明了以卡尔曼滤波与预测为载体的线性最优滤波新息序列具有零均值高斯白噪声特性。
多步新息是指利用观测量Y(k)与状态变量的T步预测量计算的差值{dT(k)}:
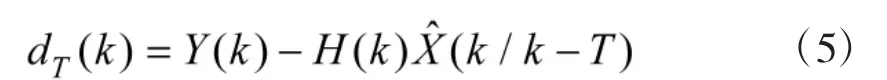
这里,T为系统运行周期的整数倍。如果目标没有作机动,对非机动目标模型来说,dT(k)同样具有零均值高斯白噪声特性,本文所描述的机动检测方法也是基于该特性。
2 机动检测方法
检测目标是否机动是一个决策问题,可以公式化为假设检验问题:
H0:目标非机动;H1:目标机动
根据观测残差和控制输入的特性,在机动目标跟踪中,很多机动检测使用χ2检验或准χ2检验,即在H0(检测机动开始)条件下,检测估计的统计量是否服从χ2分布。假设在H0条件下ε服从自由度为n 的 χ2分布(ε~χn2),且下式成立,则表明目标开始机动。

这里1-α是置信度。
归一化残差平方为。
为减少虚警和漏警的概率发生,这里采用衰减记忆统计量方法进行假设检验,记衰减记忆和为εkρ。
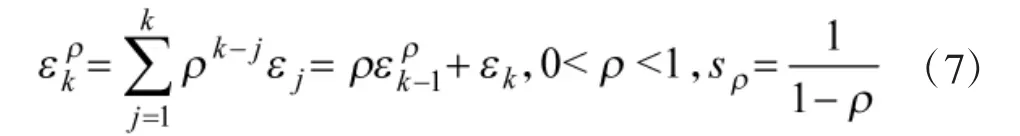
其中,ρ为衰减系数,sρ为衰减记忆和的等效窗口长度。因为 εk服从自由度为 n 的 χ2分布(即(εk~χn2,n=dim(d))。作为高斯变量的加权和 εkρ并不服从 χ2分布,但通过权匹配可将它近似看作χ2变量,即近似认为[10]
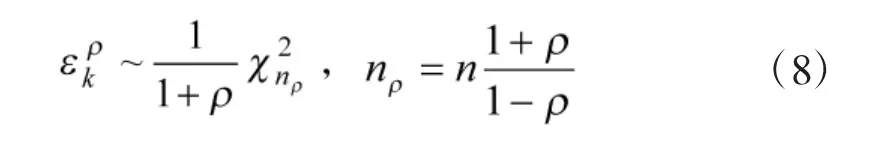
实际应用中,在球坐标系下跟踪时n=3。至此,可根据式(7)来检测机动起始,其中 ε=εkρ。
3 机动检测延迟时间
通常对假设检验问题希望获取尽可能多的测量值来提高检测概率。但对机动检测问题来说,希望尽可能快地获得判定,即获得判定的延迟最小。这样就面对两种互为矛盾的目标,即为增加检测概率而试图延迟判定,与此同时试图减小延迟来避免跟踪滞后。所以,在固定虚警率下能够准确地获取机动检测延迟时间是至关重要的。
根据式(7),可以看出εkρ的计算值与机动幅度(新息值)和窗口长度(sρ)有关,即基于 χ2检验的机动检测延迟时间是系统机动模型、机动幅度、门限值(α)和窗口长度(等价于衰减系数ρ的大小)的函数。基于多步新息的机动检测延迟时间则是系统机动模型、机动幅度(与步长也有关系)、置信度和窗口长度的函数。
置信度是根据系统要求给定的,如果选取α值较小,即置信度较高,即判定目标机动的门限值较高,因此,检测机动的延迟就大。所以,α值与机动检测延迟成反比关系。机动幅度也影响检测延迟,大机动使得新息序列的值较大,于是统计值εkρ有较大的数值。对于固定的检测门限,能更早地检测到机动。实际应用中,由于目标是未知的,从而机动幅度也是事先未知的,不能用于系统优化。当窗口长度 sρ较大时,εkρ/sρ的随机性很弱,检测滞后较大;同时若多步新息的步长较大,同样会带来检测滞后,所以多步新息的步长选择,以及窗口长度(衰减系数)的选择能优化系统。
4 仿真分析
考虑到最优问题的复杂性,这里采用仿真计算的方法,以指导步长和衰减系数的选择。
目标仿真航路是从匀速直线过渡到以某个固定过载做匀加速运动,共仿真5条目标航路,目标过载能力从1.0 g到5.0 g。对每条航路选择衰减系数从0.1到0.8不等。不同过载条件下,最小检测延迟时间与衰减系数的关系如图1所示。可以看出衰减系数越小,最小检测延迟时间越长,这也与理论分析是一致的。

图1 最小检测延迟时间与衰减系数的关系
对以上每个航路在固定衰减系数时,将多步新息的步长从10设置到60(火控运行周期的倍数)不等,并进行仿真计算。仿真结果表明:对于有显著机动的目标航路(如本文设计的那样),不同步长下的机动检测延迟时间没有变化,如表1所示;但可以显著降低目标机动检测的虚警率,如图2所示。
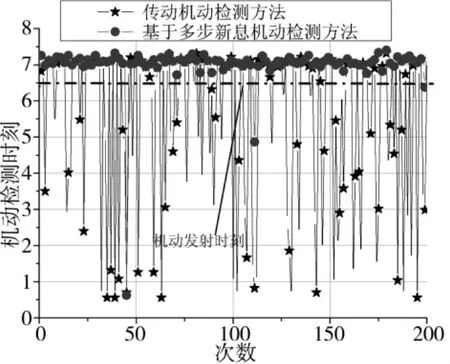
图2 基于多步新息检测方法与传统机动检测方法对比
在衰减系数为0.2时,不同航路、不同步长下的最小机动检测延迟时间如表1所示。

表1 固定衰减系数下,不同航路、不同步长下的最小机动检测延迟时间(火控运行时间)
针对弱机动航路,同样是从匀速直线过渡到以某个固定过载做匀加速运动,但目标过载只有0.2 g。在固定衰减系数条件下,最小检测延迟时间与步长的关系如图3所示。可以看出对于固定衰减系数,存在最优的预测步长。
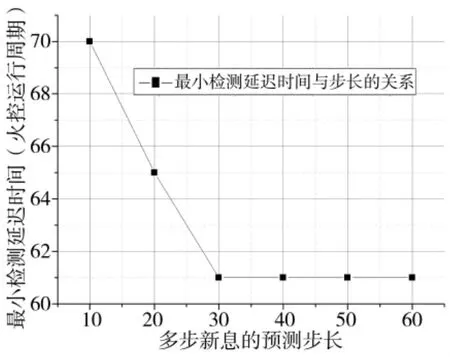
图3 最小检测延迟时间与多步新息预测步长的关系
5 结论
反舰导弹一个重要的发展方向是速度越来越快,留给末端防御系统的反应时间越来越短。为提高对反舰导弹的处理能力,一个有效的方法是提高防御系统对跟踪数据的使用率,即提高末端防御系统的数据率。但数据率的提高会降低传统基于单步新息机动检测窗口的信噪比。基于此,本文提出了基于多步新息的机动检测方法,并采用基于衰减记忆的机动检测方法。针对给定的机动检测门限,通过分析和仿真表明:基于多步新息机动检测方法可以显著降低虚警率。针对仿真航路,同时给出了最小检测延迟时间与衰减系数,以及与预测步长的关系。
[1]徐国亮.机动目标跟踪算法[J].情报指挥控制系统与仿真技术,2002,30(8):42-56.
[2]石章松,谢君.机动检测算法特性分析仿真研究[J].计算机仿真,2007,24(9):90-94.
[3]高超,邓晓波.高速机动目标检测算法研究[J].计算机仿真,2014,31(12):1-5.
[4]姚洪利,高效,田科钰.基于衰减记忆n次新息的目标机动检测和排飞点[J].情报指挥控制系统与仿真技术,2004,26(5):25-29.
[5]宋骊平,姬红兵,高新波.基于高阶累积量的目标机动检测新方法[J].电子学报,2004,32(1):154-156.
[6]李海,吴仁彪,王小寒.基于非线性最小二乘的空中机动目标检测方法 [J].电子与信息学报,2012,34(9):2143-2147.
[7]尚海燕,张雅斌,苏洪涛,等.长观测时间内机动目标检测方法 [J].系统工程与电子技术 ,2006,28(12):1779-1782.
[8]张蕊,史丽楠.基于扩展卡尔曼滤波的机动目标跟踪研究[J].航天控制,2012,30(3):12-17.
[9]岳帅,孔令讲,杨建宇,等.卡尔曼动态规划机动目标检测前跟踪方法[J].现代雷达,2011,33(6):58-63.
[10]徐国亮,邓雅娟.机动目标建模及机动检测算法[J].情报指挥控制系统与仿真技术,2005,27(4):81-83.

