融合几何成本距离并行算法的老龄化城市公共空间无障碍分析
周 蕾
(安徽新华学院 土木与环境工程学院,合肥 230088)
城市建筑物的密集程度与城市人口的增长密切相关,城市人口一旦增长,城市建筑物的密集程度就越来越密,城市空间就变得越来越小[1-2].另外,流动人口不断增加,势必造成城市空间更加狭小,让城市规划问题更加突出.科学合理的公共空间与人民的生命财产密切相关,合理专业的公共空间,不但可以减少人民群众的财产生命损失,还可以让群众死伤事件大大减少[3-5].近年来,世界范围内各个国家都加大了城市规划的研究与投入[6].采用几何成本距离并行算法无障碍分析也得到了越来越广泛的应用[7].
在几何成本距离并行算法无障碍分析中,本文以单个城市区域作为基准,将其推广到多个老龄化城市区域,在建立规划模型的过程中,其目标是疏散结束时间最小化.基于几何成本距离并行算法,对城市每个区域老龄化人流量进行恰到好处的规划,以便确定最佳的规划方案.
1 老龄化城市公共空间问题描述
1.1 问题的假设
不同的突发事件,往往具备不同的特点,在城市建筑里面,若发生火灾这种突发事件,务必及时疏散被困人员,基于这样的问题,本文特别做了以下假设:
在老龄化城市建筑中,任何一间房子都可以将其看为着火点,如果每个着火点全具有许多逃离出口,假设每个逃离通道不存在数量的约束,在此情况下,将对终极点进行定义,则此问题转化为多目标点-单个终极点的逃离规划问题.
1.2 模型的建立和转换

(1)
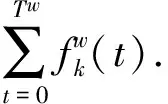
以此问题为基础,建立数学模型为
(2)

(3)
(4)

(5)
假设问题的规模足够大,一般很难列举每个障碍点到出口的全部路径,实际上也不需要列举所有路径.以舍弃问题(P)中没有被使用的路径,即流量等于0的路径,对疏散结果不产生任何影响.
如果仅仅是从公式来分析,这个问题的区别主要在路径选择方面.如果是规模较小的网络,也可以把全部的路径都一一列举出来,通常情况下,对运行时间不会带来显著的影响.如果网络规模很大,要想将路径一一列举出来,就基本上不可能了.这就意味着(P)中的路径集合可能近似无限的.
2 几何成本距离并行算法
定理1 假设P1,P2,…,Pr均为被使用,用来代表逃离人员的路径选择,在自由逃跑的路径规划方案中,每个组逃离人员所用时间总和一样,即T1=T2=…=Tr=T.若路径容量受到了限制,则可以采用单源点疏散模型算法,在这种算法中,采用的基本思路是贪婪原则,即饱和疏散最短路径.对于可行路径集合{P1,P2,…,Pm},一般采用网络更新的方式进行.具体算法流程如下:
算法1 合理的逃离路径的选择:
第一步:将逃离网络G(V,E)作为输入,如果每条弧最大容量是cij,路径选择用k表示,其值大小为1,路径集合用字母P表示,且P=Ø,对于每一条路径的流量集合用字母F表示,且F=Ø,路径疏散时间集合为TP,且TP=Ø.
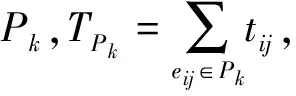
第三步:计算最大通行容量.这里的最大通行容量指的是路径Pk的最大通行容量,PCk=min{cij|eij∈Pk},令fk=PCk,F=F∪{fk};
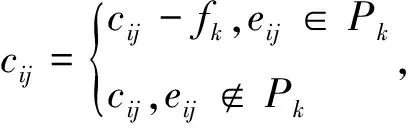
第五步:选择循环.若更新的网络不连通,则转入第六步执行,若更新的网络是连通的,则令k=k+1,并将其转入第二步执行.
第六步:将P、TP、F的值输出.
fk一般是一个常数,由几何成本距离并行算法技术可知,设t时刻离开路径Pk,抵达D0的总人数xk(t)满足如下表达式:
(6)
假设x是等待疏散的被困人员总数,那么路径m1满足如下表达式:
(7)
对于实际参与疏散的路径集合{P1,P2,…,Pm1}我们可以利用式(7)进行确定.
定理2 采用可行路径算法所确定的路径集合,用字母P表示,且任意一条路径都满足Pk∉P,那么,增加Pk必然无法改善疏散方案.
定理3 假设可行路径集合P是通过算法1来确定的,且在P中的元素满足:TP1≤TP2≤…≤TPm.则式(7)所确定的路径P1,P2,…,Pm1(m1≤m)在所有的路径中,才是最佳的疏散路径.
通过定理1的分析可知,最后一人到达终极终点D0的时间是一样的,假设结束时间是T,结合定理3,可得
(8)
由式(8)解得:
(9)
从以上式子可以得出:只要对实际逃离路线选择,那么逃离结束的时间就能够进行确定,同时参考xk(T)=(T-(TPk-1))fk,则能够确定最优逃离策略.
3 应用实例
下面本文将通过相关的例子来验证算法的可行性与合理性.如图1所示,它所表示的是一个城市建筑的平面图形,弧上面所表示的数字代表的是弧(指图1中建筑示意图上带有方向箭头的弧形)的标号.节点类型与描述详见表1.
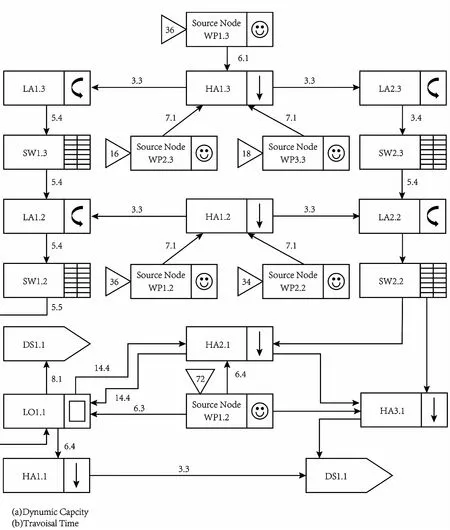
图1 老龄化城市建筑疏散例子

表1 节点描述
每个房屋实际参与疏散的路径可以采用算法1对其确定,具体内容见表2;在需要优先饱和疏散所需时间(time)长的房屋,对各个时刻各条路径上的实际流量进行了确定.详见表3,并最终确定T1=11,T2=32,T3=34(表示的是每个房屋疏散结束时间),同时确定T=max{Tw}=34(指的是最后疏散结束时间).
4 结论
本文在相关算法与相关论证的基础上建立的老龄化城市建筑模型,基于超级终点,将相关问题转换为单个区域老龄化城市的规划问题.文中采用了几何成本距离并行算法的无障碍分析,对公共空间的容量进行实时更新,并对实际参与规划的老龄人进行合理的确定,再通过专业无障碍分析对实时流量进行计算,确定最终规划方案.最后例子验证了本文所提算法的科学性与合理性.

表2 实际参与的疏散路径集合Kw和疏散结束时间Tw
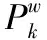
表3 路径的老龄化流量
[参 考 文 献]
[1] KARIMINIA S,SHAMSHIRBAND S,MOTAMEDI S,et al.A systematic extreme learning machine approach to analyze visitors. thermal comfort at a public urban space[J].Renewable & Sustainable Energy Reviews,2016,58:751-760.
[2] LONGO V D,SHADEL G S,KAEBERLEINM,et al.Replicative and chronological aging in saccharomyces cerevisiae[J].Cell Metabolism,2012,16(1):18-31.
[3] EKMAN M R,LUNDéN P,NILSSON M E.Similarity and pleasantness assessments of water-fountain sounds recorded in urban public spaces[J].Journal of the Acoustical Society ofAmerica,2015,138(5):3043-3052.
[4] LONGO V D,SHADEL G S,KAEBERLEIN M,et al.Replicative and chronological aging in saccharomyces cerevisiae[J].Cell Metabolism,2012,16(1):18-31.
[5] RICCITELLI M L.Visualizing the experience and use of space in the built environment[J].Journal of the American Geriatrics Society,2015,11(4):299-302.
[6] WIDHALM P,YANG Y,ULM M,et al.Discovering urban activity patterns in cell phone data[J].Transportation,2015,42(4):597-623.
[7] SHANAHAN D F,FULLER R A,BUSH R,et al..The health benefits of urban nature:how much do we need?[J].Bioscience,2015,65(5):476-485.

