意外考试悖论和认识论问题

陶 昱

（北京大学 物理学院，北京 100871）

一、意外考试悖论和它的变形

意外考试悖论（the surprise exam paradox）在历史上有多个类似版本，如“突然演习悖论”“意外绞刑悖论”和“求婚者悖论”等。意外考试悖论由哲学家奥康纳 （D.J.O’Connor）于1948年正式提出，并以“语用悖论”（pragmatic paradox）称谓之。1953年，另一位哲学家蒯因 （W.V.O.Quine）将此悖论从认知的角度重新提起，引起了热烈的讨论，于是意外考试悖论被作为认知悖论而受到学界的重视。

意外考试悖论是这样的：一位老师对学生宣布，在下周的5个工作日内要考试，但哪一天不确定；这位老师宣称，考试时间是不能被预测到的。一位学生这样想：老师一定不会在下周五考试，因为如果前4天不考试的话，星期五考试就成为可预测的；如果星期五不考试，那么星期四也不会考试，因为如果前3天和星期五不考试，那么星期四考试就成为可预测的。以此类推，星期一也不会考试，因为如果后4天不考试，那么星期一考试就成为可预测的。这样，老师每一天都不会考试。然而，这又同老师关于下一周内必有考试的承诺相违背。这意味着，老师必有考试的承诺和让考试日期不可预测的承诺之间是相矛盾的。这就是意外考试悖论［1-2］。

意外考试悖论还有若干变形，例如 “例外演习”悖论、“方片A扑克牌”①即一个人拿着一堆牌向另一个人一张一张地翻开，宣称“你不可能提前知道下一张翻到的是方片A”，推理过程与意外考试悖论类似。悖论［3］、“被选中的学生”悖论等。大多数变形和原来的悖论实质上相差不大，值得引起注意的是“被选中的学生”悖论，让整个推理的过程不再需要考虑人的认知水平随时间的变化，这对于研究意外考试悖论具有重要意义。

除此之外，有人直接从哥德尔不完备性定理出发来论证这个悖论［4］，有人将它和“薛定谔的猫”的悖论联系起来［5］。

二、先前关于解决意外考试悖论的工作

（一）通过“二阶主体操作”的理论来解决

先前，陈晓平将悖论按照其逻辑形式分为“一阶”和“二阶”悖论［1］。悖论的描述当中只涉及到对象语言的称为“一阶悖论”，比如“A既是B又不是 B”。悖论当中涉及到元语言的称为“二阶悖论”，比如“这句话是一句假话”，按照其语义分为“客观描述悖论”和“主体操作悖论”。悖论只涉及到客观描述的称作“客观描述悖论”，涉及到操作问题的称为“操作悖论”。意外考试悖论和一系列认知悖论被划入“二阶主体操作悖论”的范畴。由于老师的宣告“被遵守就意味着被违反，被违反就意味着被遵守”，因此它是“不可操作的”，并且由于操作的封闭性，“不可操作也是一种操作”，因此就解决了这个悖论。

本人认为这样的解决方案其实并不能令人满意。首先，该方案认为“认知悖论这种分类方法是模糊的”，与实际情况不相符合。事实上，人的“认知”成为一个重要哲学概念的时间由来已久，在古希腊时期柏拉图就有“知识是可以证明的真信念”的论断，近代又产生了知识的JTB（justified true belief）理论和各种对于JTB知识论的质疑和补充。所谓“认知悖论”就是直接指向人的“知识”这一概念的悖论，这里没有什么“模糊”的地方，强行将这些悖论划归到“语义悖论”和“操作悖论”的范畴当中，看起来没什么道理。

其次，“操作具有封闭性”这一个假设也缺乏依据和其他工作的支持，尤其是如果已经从其中得出了“不可操作也是一种操作”这样看起来比较荒谬的结论，就更说明这个假设可能存在问题。陈晓平认为引入与认知有关的谓词，建立认知的逻辑“与人类的直觉相去甚远”，但是这里关于“操作”的概念可能更加远离人类的直觉。从“操作”的字面意义上来理解，由于“不可操作”这个论断本身并没有做出任何的操作，因此将它也当成一种操作看起来并不合理。

并且，陈晓平在文中已经承认“老师的宣告被遵守就意味着被违反”，这就已经是意外考试悖论最为核心的问题了。因为从直觉来看，老师的宣告是可以不在任何程度上被违反的，如果已经假设了“老师的宣告被遵守就意味着被违反”，就意味着默认了意外考试悖论里面最为荒谬的地方，在此情况下，得到了“不可操作也是一种操作”，并不能被认为就解决了这个悖论。

总而言之，通过新建一个概念，生硬地做出一些假设，在新建立的这个体系中说明悖论已经被解决，并且既不说明旧的体系的问题，也不说明建立新的体系的技术性以外的动机，这个方法是平庸 （trivial）的，不是一个令人满意的解决方案。

（二）通过转移矛盾来解决

蒯因提出，在这个悖论当中学生所否定的实际上并非教师的宣告本身，而仅仅是“学生在教师宣告之后，立刻知道教师的宣告为真”这一假定［6-7］。也就是说，在教师宣告之后，学生所做的推理仅仅能够得到的结论是“教师的宣告为真”这一个断言，但这还不能够成为学生的知识，学生并不“知道”教师的宣告是否为真。

但是，本人认为这样的解决方案也不令人满意，因为这会导致其他与人的直觉相矛盾的结论。最严重的是，这里所产生的“知识”的概念与常识和直觉上的“知识”并不一致。从直觉上来讲，学生是应该知道老师的宣告为真的，没有证据证明老师在说谎，并且教师所做出的宣告，确实有实现的可能性：试想，老师在下周三考试，那么从直觉上讲，学生并不可能在前两天都没有发生考试的情况下，在周二晚上就“知道”周三会进行考试。在这种情况下，周三的考试对于学生来讲确实是“意外”的。“学生并不能以教师所做出的宣告不能实现为理由为自己在考试中发挥失常推脱。”［3］并且学生在老师宣告之后，就可以立即预见到可能周三考试的状况，预见到从直觉上自己并不能在前两天都没有发生考试的情况下，在周二晚上就“知道”周三会进行考试的情况，因此学生立刻就可以知道，教师的宣告是可以被实现的。

另外，学生根据自己的逻辑推理，又可以在教师宣告之后立即知道教师的宣告是不可以实现的。因此，抛开学生是否知道教师的宣告为真的问题，只需要考虑学生知道老师的宣告是否有可能实现的问题，就足以导出反直觉的结论：学生的知识产生了自相矛盾，然而自相矛盾的两个方面，“教师的宣告可能实现”来源于看起来没有问题的直觉，而“教师的宣告不可能的实现”来源于从看起来没有问题的直觉出发的逻辑演绎。

诚然，蒯因通过转移矛盾避免了直接演绎得到一个矛盾式，情况变成了只是在学生的知识中出现了矛盾。然而，这样的解决方案只解决了这个悖论的一部分，还不是一个完全的解决方案；它只是削弱了矛盾，而非解决了矛盾。因为仅仅是学生在认识上的自相矛盾就已经是一个令人不能接受的结论了。这个矛盾说明了人类完全符合直觉和逻辑的认知过程有可能产生完全矛盾的知识（教师的宣告事实上不可能既有可能实现又不可能实现）。如果不能直接解决这个问题，或者不能将可靠的和不可靠的认知过程区分开来，就意味着人类所掌握的所有知识都将成为不可靠的知识，这是不能接受的结论。

另外，“悖论是从一组看似合理的前提出发，经过有效的逻辑推导，得出了一对自相矛盾的结论的命题”［2］。我们还需要注意到，“学生知道老师的宣告为真”本来也是“看似正确”的前提之一。除了从逻辑上否定它，还必须找出它的问题，而蒯因的工作仿佛并没有直接说明这个命题有什么不对的地方。

总而言之，蒯因的解决方案的缺陷与之前所述的操作理论解决方案的缺陷有相似之处，即都回避了这个悖论中最重要的问题：为什么老师的宣告会有问题？事实上，把解决方法归结于“受到否定的只是老师的宣告”，无异于将悖论的矛盾之处从一个点转移到了另一个点，并没有解决矛盾。

（三）通过拒斥知识的持久性来解决

克里普克试图通过拒斥知识的持久性来解决这个悖论。他首先分析了这个悖论依赖的一些关于知识的前提条件，也就是“公认正确的背景知识”，共有10条：

（1）教师宣布考试将在下一周的某个时间举行；

（2）考试将在下一周某个确切的时间举行；

（3）学生在举行考试的前一天并不知道考试将在第二天举行；

（4）如果前i-1天都没有考试，那么学生在第i-1天知道这个事实；

（5）如果某一天发生了考试，那么这一天的前面的日子没有考试；

（6）凡是学生知道的东西都是真的；

（7）如果学生知道a并且a蕴含b，那么学生知道b；

（8）学生知道所有的逻辑重言式；

（9）如果学生在某个时候有某个知识，那么他在这个时刻之后的每一个时刻都有这个知识；

（10）如果学生知道a，那么他知道自己知道a。

从这10条出发，就可以得出矛盾。克里普克对于其中的第9条（如果学生在某个时候有某个知识，那么他在这个时刻之后的每一个时刻都有这个知识），也就是对知识的持久性提出了怀疑。由于一个认知主体在时间流逝中可能会发现新的证据，并用它来反对自己之前所拥有的知识，所以知识并不是持久的。虽然有“知道蕴含真理”的原则，而且真理是不会改变的，但是人对于真理的信念的强度确实会受到所见的证据的影响，有可能转而对真理采取不相信的态度，因此拒斥原则9是有一定的依据的。美中不足的是，仿佛没有人说明，在得出谬误的过程中，究竟有什么新的证据足以消除认知主体过去拥有的关于举行考试的情况的知识。

然而，索伦森将这个悖论变形，构造了一个“被选中的学生”的新的悖论，从而完全避开了知识随时间变化的问题［7-8］。

“被选中的学生”是这样的一个情形：有n个学生排成一列，教师在他们每个人后背上贴了一个五角星，只有一个同学背后的五角星是金色的，这个同学就是被选中的同学。每一个同学只能看见前面同学背后的五角星颜色，看不见自己的和后面同学的。教师宣告，这位被选中的同学并不知道自己被选中了。

然而，根据逻辑推理，每一位同学都知道这是不可能的。如果金色五角星贴在最后一位同学后背上，那么他看见前面的同学后背就知道了自己被选中了，因此被选中的不是最后一位同学。如果被选中的是倒数第二位，由于他明知最后一位同学不可能被选中，又看见之前的同学都没有被选中，就知道自己被选中了，因此他也不是被选中的。由此类推可以得到被选中的只能是最前面的同学，这样一来他就知道了自己被选中，因此教师的宣告不能成立。

“被选中的学生”悖论在推理过程中将时间的前后转换成空间的前后关系，因此避免了知识随时间变化的问题，而且其中的每一个“不可能选中第X个学生”的结论都是所有学生共同的知识。

除了索伦森之外，还有人通过质疑JTB知识论，或者质疑最后一条规则（也被称为正内省原则）来质疑克里普克的解决方案，但正如文献［3］中指出的一样，这样的论点实际上不足以构成对于克里普克的解决方案的质疑。

总而言之，由于索伦森的工作，克里普克虽然找到了一个解决意外考试悖论的方法，但是他的解决方案却不能解决一个和意外考试悖论极为类似的悖论，不具有可以推广的性质。为了解决这一类悖论，还需要做更多的工作。

三、通过形式认知系统寻找矛盾

（一）形式系统的建立

克里普克对意外考试悖论的解决方案被索伦森构造的新悖论反驳，说明他的解决方案也许并未触及这个悖论的本质。进一步可以断言，通过修改人的知识和时序的关系来解决这个悖论并不能触及到这个问题的本质。本文拟通过在一阶算术系统的基础上建立形式系统的方式来分析形成这个悖论的每一个前提的可靠性，进而研究拒斥某一些原则的解决方案。哥德尔在证明不完全性定理中所做的工作表明，我们可以通过编码的方式将所有的元语言全部用自然数来表示，称为对字符串进行哥德尔编码。又由于一个函数的可计算性、可表达性和递归性三者之间存在等价关系，元语言中的清晰地表达对象关系的语句也可以用一阶算术的形式表达。利用这种思想，我们可以将关于人类认知的理论形式化，事实上克里普克已经给出了意外考试悖论对应的形式系统［7］。

事实上，通过形式系统来研究悖论有重要的意义，因为通过严密的逻辑推理，可以清晰地看见达成悖论所需要的所有前提，可以排除在推理的过程中自相矛盾的情况，这样就可以用一种分析的方法来看待悖论的问题。对“被选中的学生”，也可以模仿克里普克的工作来建立这样一个形式系统：除了一阶算术已有的谓词和公理之外，加入n个1元谓词 K1，K2，…，Kn，此处Ki（x）解释为第i个学生知道哥德尔编码为x的这一个公式①在本文当中，我们在谓词K当中用一个公式代表它的哥德尔编码，例如K1（p p）实际上代表的是K1（m），其中m是公式p p的哥德尔编码。；并加入n个0元谓词 （也就是命题），P1，P2，…，Pn，此处Pi解释为金色五角星粘贴在第i个同学背上。

在克里普克所提出的几个公理当中，以下几条是关于人类的认识规律的①（C1—C3）每一条都对应着若干条公理，因为公式中的i，j，k…可以分别取1-n的整数值，之后的（H1-H5）也是如此。：

对“被选中的学生”这个特殊的情形，由于学生对游戏规则知情，还有这么几条基本假设（模式）：

在开始推理之前有几点需要说明：

首先，在工作当中徐召清曾指出，“知识的合取规则”，也就是 （K（A） K（B））→K（A B）应当作为一条新的原则被引入［3］。本人认为这是没有必要的，因为这一命题是前述的公理和形式算术其他公理的逻辑后承。在此有必要证明一下这个结论。之后，将知识的合取规则记为（CK）。

命题1

证明 由于一阶逻辑的演绎定理，只需要证明

事实上，可以做这样的演绎：

因此，结论成立。

由于 （CK）是 （C1）（C2）（C3）的后承，又考虑到 （C4），因此可以认为每一个同学都知道知识的合取规则。其次，在关于知识的公理（C1—C3）当中并没有之前所说的“正内省原则”，这是因为实际上在“被选中的学生”这一个具体的悖论问题当中，并不需要一个普遍的正内省原则，而且在之前克里普克关于“意外考试悖论”的推理当中也并没有出现这一个假定［3］。但是，知识的正内省性质可能在其他涉及到知识论的场合很重要。另外，（C4）和（H5）事实上是正内省原则在本问题当中的一个特例。普遍的正内省原则受到了很多质疑，但是这个特例看起来易于接受。这也从另一个侧面说明，普遍的知识正内省原则并非“被选中的学生”悖论的关键。

其次，有必要对于几个假设的公式给出解释。（H1）可以解释为，每一个学生都知道在所有学生当中至少有一个学生被选中；（H2）可以解释为，每一个学生都知道不可能有两个学生同时被选中；（H3）可以解释为，每一个学生都知道被选中的那个人不知道自己被选中了；（H4）可以解释为，每一个同学都知道以下事实：如果某一个同学背后没有贴金色的五角星，那么所有他后面的同学都可以看到他没有贴金色的五角星；（H5）可以解释为每一个同学都知道任何一个同学对游戏规则是知情的。

（二）形式系统的演绎

有必要验证之前建立的形式系统，从它的假设出发是否能够导出矛盾。我们分若干部分来证明。

命题2

证明 在之前的证明中，可以发现A B可以作为A和B的逻辑后承。之后把这个规则记为CD，不再说明。

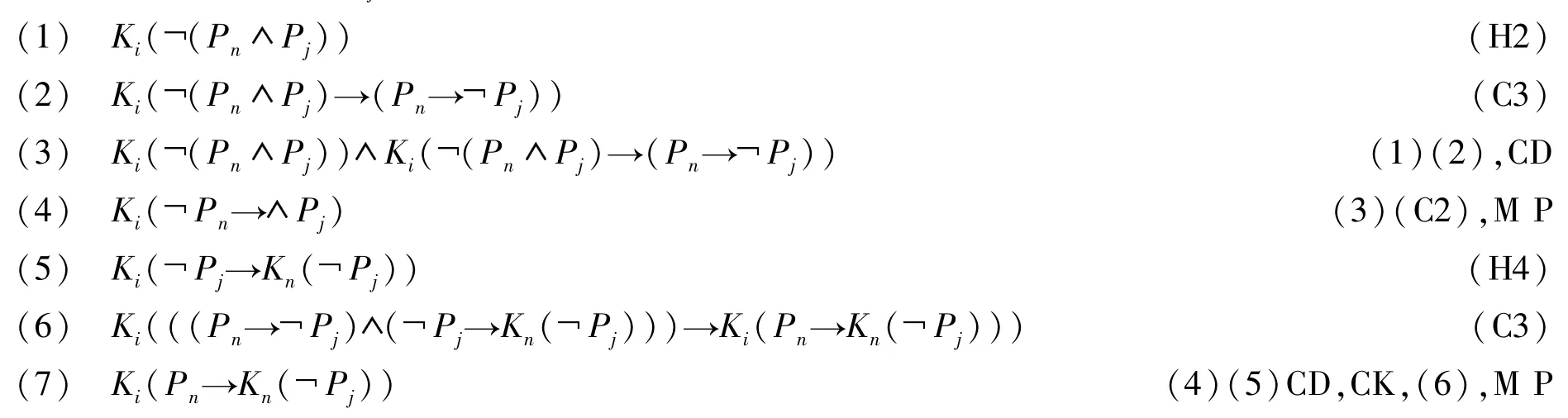
先证明 Ki（Pn→Kn（ Pj））（j＜n）。事实上可以如下演绎：因此有Ki（Pn→Kn（ P1）），Ki（Pn→Kn（ P2）），…，Ki（Pn→Kn（ Pn-1））。由于（A→B）（A→C）→（A→（B C））是一个重言式，反复运用知识合取规则和（C2）就可以将这n-1个命题合并成一个命题，也就是 Ki（Pn→Kn（ P1P2… Pn-1））。

命题3

证明 事实上可以做如下演绎。为了缩减篇幅，用 A表示 Kn（ P1（ P2… Pn-1），B表示Kn（P1P2… Pn），C表示 Kn（（P1… Pn）（ P1… Pn-1））。

由此我们可以得出，每一个同学都知道，如果最后一个同学被选中，那么他知道他自己被选中了，这正是之前非形式化论述悖论时的一步。

命题4

证明 演绎如下：

因此，我们演绎后得到的结论是：每一个同学都知道被选中的人只能在前n-1个同学当中。

命题5

证明 我们经过刚才的演绎，事实上得到了：

根据一阶逻辑演绎定理就有：

下面，对于n使用数学归纳法来证明：

n＝1 由于A→A是重言式，显然成立。

假设对于n＝k，命题成立。由之前的演绎我们知道：

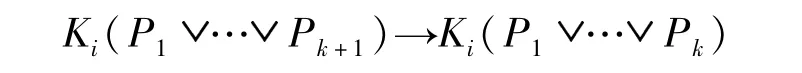
根据归纳假设，

运用假言三段论（HS）就有：

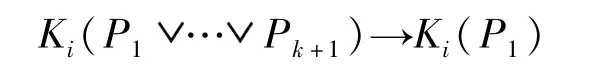
由数学归纳法，结论成立，再由演绎定理知Ki（P1）。

特别地，有K1（P1）。再进一步演绎就可以导出矛盾。

命题6

证明 事实上可以这样演绎：

这样就演绎得到了矛盾式P1P1。因此我们可以说，这样的结果不仅是“反直觉”的，而且是“自相矛盾”的。这说明我们采用的9条假设相互之间并不相容，因此有必要考察它们中的每一条，验证它们的可靠性。

（三）对于各种修改方案的讨论

（C1）—（C4）是关于每一个同学认知能力的基本假设。其中，（C1）代表同学相信的都是正确的，这一条假设仿佛正确性得不到保障，并且假设教师选中了第五个人，那么通过刚才的演绎过程，中间得到的同学的某一些知识与事实是相反的，比如前四个、前三个、前两个同学当中都没有被选中的同学。事实上，如果舍弃（C1），那么即使得到了“第一个同学知道自己被选中”的结论也不能导出逻辑上的不一致，只能够导出同学在认识上的不一致和矛盾①导出认识上的矛盾可能还需要知识的正内省原则。。“知识蕴含真理”这一条假设也确实受到了很大的质疑，因为从常识上来讲人确实经常产生错误的认识。删除（C1）仿佛是一个不错的解决方案。

然而，这里的“知道”并不完全是日常生活中的“知道”。这里同学们所“知道”的内容都是从其他几条假设出发，经过了严格的逻辑演绎过程得到的结论，所依赖的前提也仅仅是游戏规则和很难说有什么错误的自己亲眼所见前面同学背后没有金色五角星的事实。实际上，如果舍弃了“经过严格的逻辑演绎得到的结论是真的”的假设，那么几乎没有什么东西是真的了。“从真的知识出发经过合法的演绎过程得到的结论是知识（也就是真理）”是人类思维当中极其基本的原则，舍弃它会给其他场合下解决问题带来很大的困难，而且从直觉上讲这一条也不应该被舍弃，因此是否舍弃 （C1）是一个可以接受的解决方案还有待考虑。

（C2）（C3）是关于同学们逻辑演绎能力的公理，同时也代表着一个人相信自己演绎的结果。这也同样是非常基本的假设，而且同学们显然也应该具有逻辑演绎的能力并相信自己的结果。虽然确实有人提出了通过拒斥认知的封闭性来解决悖论的解决方案［7］，但是如同知识的正内省原则一样，这个悖论事实上并没有用到普遍的认知封闭性的原则，只用到了它的若干个特例②由于用到的特例数量众多，如果一一列举将会使得篇幅过长，因此本文中仅用了一个普遍的公理模式来表示。，并且并没有证据表明其中任何一步的推理是错误的③这里的情况仿佛与连锁悖论有接近的地方，冗长的推理过程没有任何一步有明显问题，但是推出了荒谬的结论，然而正如文献［3］所谈到的，推理的过程没有任何的模糊性，因而也无法用解决连锁悖论的方法来解决这个悖论。，因此删除它们不是可以接受的解决方法。

（C4）则是说明每个同学都知道其他同学有充分的认知能力。如同之前所论证的，这是正内省原则的一个特例，比起普遍的正内省原则可靠很多，这也不是一个可以舍弃的公理。

在（H1）—（H5）之中，（H3）的可靠性是最得不到保障的④当然，如果（H3）的可靠性有待商榷，那么包含（H3）的（H5）的可靠性也是同样的。。（H3）是想要表述“被选中的同学不知道自己被选中”的事实，采用了“如果第i个同学被选中，那么他不知道自己被选中”的形式。这样的一个形式是否恰如其分地捕捉到了“被选中的同学不知道自己被选中”这一句话的语义，从直观上看来并不能确定。

一种想法是采用 Ki（Pi）的形式，但是正文中的（H3）是它的后承 （因为A→（B→A）是重言式），因此从这一个条件出发同样导致矛盾。

鉴于“被选中的学生不知道自己被选中”这句话只对一个学生对于自己有没有被选中的认知情况做出了断言，而（H3）实际上对每一个学生对自己有没有被选中的认知情况做出了一定程度的断言，另一个可能产生的想法是，让（H3）只涉及到一个同学，这就需要将同学的编号作为变量引入，即将Pi改为P（i），Ki（m）改为 K（i，m），然后将假设改为

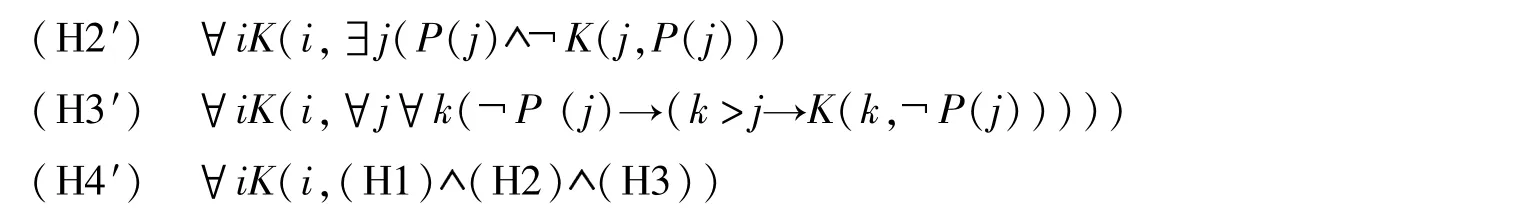
（H1′） ∀iK（i，∃！j（P（j）））可能可以更好地捕捉“被选中的学生不知道自己被选中”的意思。事实上，在这样修改之后，先前用于导出矛盾的演绎过程不再适用，而且本人没有找出从这4条假设出发得到矛盾的演绎方法，也没有找出这个公理体系的模型，因此这几个假设和 （C1）—（C3）是否一致还有待进一步证明。

这样的方法也有问题，比如同学数量是有限的，但是一阶逻辑的变量的取值范围很可能是无穷的。除此之外，认知封闭性的原则，可能需要复杂的修改，因为在引入变量之后，如果公式A不是闭公式，那么一般不能从AB得出A→B，然而 AB本身并不是一个一阶逻辑公式。另外，需要给这个形式系统也赋予意义，这必须要用到一阶逻辑的模型。在一阶逻辑的任何一个模型当中都必须给谓词P明确地赋值，因而也就明确了哪一个同学被选中，这就意味着任何一个模型都没有“有一个同学被选中但是不知道是哪一个”的情况。

也许在表达当中蕴含模糊性，也可以更好地表达“被选中的学生不知道自己被选中”这句话的意思。这既有可能通过在一阶逻辑中引入模糊性谓词来实现，也有可能通过在模态逻辑中引入代表模糊性的符号来实现。引入模糊性，也许还可以运用解决连锁悖论的方案来解决这个问题①与之前提到的模糊性不同，这里的模糊性并非隐含在推理过程中，而是从推理的源头（也就是假设）开始的。。这里引入模糊性并不是没有理由的技术性处理，而是因为如之前所说，“被选中的学生不知道自己被选中”这句话确实有一定的模糊性。

从技术层面来讲，拒斥（H1）或者（H2）也是中断推理过程从而避免矛盾的方法之一。事实上，这就是拒斥了“学生知道老师的宣告为真”的假设，因为老师的宣告可以分为3个部分：“所有同学当中有人被选中了”；“只有一个同学被选中”；“被选中的同学不知道自己被选中”。最后一个与（H3）相关，而前两个与（H1）（H2）相关，并且从直觉上来讲这两个一阶逻辑公式非常精确地表达了“同学知道有人被选中”和“同学知道不可能有两个人同时被选中”的意思，因此拒斥它们就等同于拒斥“学生知道老师的宣告为真”。这实际上就是蒯因的解决方案，如之前的论证所说的，这并不是一个令人满意的解决方案。

至于还在演绎中用到了的“重言式”、形式算术系统的各个公理、三段论的分离规则以及假言三段论等推理规则，则是比起（C1—C3）、（H1—H5）更加基础和重要的原则，舍弃它们同样不是可以接受的解决方案。当然，如果引入了其他的逻辑系统，其中的推理规则等有所不同，也就等于拒斥了这些公理中的一部分。

总而言之，在检查了每一条假设之后，有两种解决方案看起来是有可能被接受的，值得继续深入研究。一种是将同学的编号i量化，在含有变量的公式中进行逻辑演绎；另一种是引入模糊性谓词或者符号来扩充这个形式逻辑系统。两者的出发点都是（H3）并没有精确地表示“被选中的同学不知道自己被选中”这句话当中“被选中的同学”这个概念的模糊性。然而，前者在利用模型来解释含义的时候还会遇到问题，而两者都由于作者水平有限，无法独立验证其是否可行，只有留待以后的研究来检验。

四、结语

本文回顾了“意外考试悖论”的提出及其一些解决方案。本来克里普克的拒斥知识持久性的解决方案是一个不错的解决方案，但是由于索伦森构造的“被选中的学生”的悖论，这个方案也变得不令人满意，于是本文模仿克里普克的工作建立了一个针对“被选中的学生”的公理系统，并且验证了从中确实可以导出矛盾。本文还就建立的公理体系讨论了解决索伦森提出的悖论的方案，并且指出了舍弃“知识蕴含真理”的原则，引入变量，或者利用比一阶逻辑更加复杂的逻辑系统来修改对于游戏规则的表述的解决方案的优劣。

然而，本文的工作也是很有局限的，最严重的是未能直接检验引入变量或者利用带有模糊性的逻辑是否能够解决悖论，这个工作只有留待以后完成了。

致谢：感谢北京大学哲学系陈波教授和四川大学公共管理学院徐召清副教授在本文撰写过程中给予的帮助。

［1］ 陈晓平.意外考试悖论及其解决［J］.湖南科技大学学报（社会科学版），2013，16（3）：25-30.

［2］ 陈波.悖论研究［M］.北京：北京大学出版社，2017.

［5］ 徐召清.克里普克意外考试悖论［J］.河南社会科学，2016，24（8）：71-76.

［4］ CHOW T Y.The surprise examination or unexpected hanging paradox［J］.The American Math-ematical Monthly，1998，105（1）：41-51.

［5］ HOLTZMAN J M.A note on schrödinger’s cat and the unexpected hanging paradox［J］.British Journal for the Philosophy of Science，1988，39（3）：397-401.

［6］ QUINE WV.On a so-called paradox［J］.Mind，1953，62（9）：65-67.

［7］ 杜国平，雒自新.“意外考试悖论”研究进展［J］.哲学动态，2015（5）：96-101.

［8］ SORENSEN R A.Conditional blindspots and the knowledge squeeze：A solution to the prediction paradox［J］.Australasian Journal of Philosophy，1984，62（2）：126-135.