基于CTMC族的多部件装备群稳态可用度建模方法

冯 晓, 郭霖瀚, 宋常浩, 孔丹丹

(1. 北京航空航天大学可靠性与系统工程学院, 北京 100191;2. 中国电子科技集团公司第十四研究所, 江苏 南京 210039)

0 引 言

为了完成特定的使用任务要求,往往需要包含多个相同功能装备的装备群[1]来执行工作。可用度是指装备群在任一时刻开始执行任务时,处于可工作或可使用状态的概率度量。针对连续工作的装备群来说,稳态可用度可以被用来表征装备群的可用程度。因此准确计算其稳态可用度对装备群的设计、运行和管理均具有显著的理论意义和实用价值。

当装备的各部件寿命分布和故障后的修理时间分布均为指数分布时,只要合理定义装备的状态,便可以使用马尔可夫过程来描述装备,从而进行稳态可用度的建模和求解。文献[2-3]针对串联、并联等系统,在不考虑备件库存的条件下利用马尔可夫过程建模,计算系统稳态可用度和瞬时可用度。文献[4]以单部件可修系统为研究对象,假设维修时间小于给定的常数时可以忽略,从而计算系统的稳态可用度。文献[5-8]分别研究了两类部件串联的系统稳态可用度计算问题。文献[9]给出了n个部件串联的系统瞬时可用度和稳态可用度的表达式。文献[10]研究了一种计算含有混合冷温备件的多部件系统稳态可用度的方法。文献[11]研究了包含3个不相同的部件、带有优先权的串并联可修系统,通过使用补充变量法和矢量马尔可夫过程理论计算系统的稳态可用度。文献[12-17]分别研究了k/n表决系统稳态可用度计算问题。文献[18]中通过连续时间马尔可夫链来描述系统的有限状态,使用两种方法分析长期使用的可修系统稳态可用度。

目前利用马尔可夫过程研究稳态可用度时,考虑可修件库存影响的并不多,但在实际维修过程中,经常出现由于等待或缺少备件造成维修延误的情况,导致系统可用性降低。此外,现有文献提供的方法多是利用马尔可夫过程对单个系统进行可用度分析。由于装备群中的装备共用给定的备件资源,当某类备件出现短缺后,可用装备的数量会随之发生变化。因此无法通过计算单个装备的可用度来求解考虑备件库存影响下的装备群可用度。

针对以上这些问题,本文考虑备件库存影响,构建一种基于多个连续时间马尔可夫链(continuous time Markov chain,CTMC)的模型来分析装备群稳态可用度。首先,考虑装备群中部件使用与维修的特点,采用可用装备数、备件库存数、备件短缺数3个参数来刻画部件的状态,对各类部件分别建立CTMC,进而建立装备群的CTMC族模型;其次,根据各类部件的转移率矩阵,求解各状态稳态概率,并结合部件的期望备件短缺数(expected backorder,EBO)与可用装备数之间的关系确定装备群稳态可用度;再次,构造案例进行仿真验证分析;最后,提出结论和未来的研究工作方向。

1 模型假定与说明

本文的研究对象是由N个同型的多部件装备组成的装备群。当执行任务时,装备群中的装备相互独立地开展内容相同的工作。每个装备由L类不同的关键部件串联组成,其中第i类部件的单装备安装数为Zi,初始库存数为Si。当备件不短缺时,直接使用备件来更换故障部件;当备件短缺时,需等待故障的部件维修好后,装备才能重新执行任务。建模过程中考虑以下假设:

假设1部件及其备件均可修,且维修后能够修复如新,不考虑报废问题。

假设2第i类部件的故障间隔时间服从参数为λi的指数分布,维修时间服从参数为μi的指数分布。

假设3装备群工作时间连续。

假设4除备件外其他维修资源均供应充足,并且修理能力无限。

假设5库存结构为单基地模型,备件实行(s-1,s)及时送修策略。

假设6忽略故障件的更换时间。

由库存平衡公式[19]BOi=OHi+DIi-Si可知,利用部件i的现有库存量OHi、在修故障件数DIi以及部件的初始库存量Si可以计算部件i的备件短缺数BOi。当部件i发生一次备件需求时,DIi就增加一件;若OHi≥1,则OHi就会减少一件;否则,BOi就增加一件。初始库存量Si根据费用、库存空间等约束提前确定。任意一类部件出现故障后,当备件不短缺时,直接使用备件来更换故障部件;当备件短缺后,该类部件的备件短缺数和在修故障件数均加1,则装配该故障部件的装备将处于故障维修状态,导致装备群中可用的装备数减1。因此根据部件的备件短缺数、现有库存量、在修件数与可用装备数的上述关系,对带有备件的装备群进行马尔可夫过程建模时,描述状态的粒度可由装备群细化到各类部件,从而避免直接对装备群建模。

当各类部件的初始备件库存为零时,如果考虑备件短缺对可用装备数造成的影响,基于各类部件的CTMC建立装备群的CTMC族模型,状态空间规模将随部件种类数L的增加呈线性增长;反之,基于马尔可夫过程直接对装备群进行建模,状态空间的规模将随L的增加呈指数增长。当各类部件有初始备件库存时,使用前者方法得到的状态空间将远小于后者。故本文提出的模型将能够显著减少状态空间的规模,从而降低计算稳态可用度的复杂度。

2 稳态可用度的建模

2.1 装备群的CTMC族模型

初始时刻装备群中的N个装备都能正常执行任务。在执行任务过程中,部件i(1≤i≤L)的状态由Oi,Gi,BOi3个参数表示。其中，Oi表示受部件i影响的可用装备数,0≤Oi≤N。Oi的取值与部件i的在修件数DIi有关。当DIi≤Si时,Oi=N;当DIi≥Si+1时,部件i每出现一次故障将导致一个装备停机等待维修,Oi的取值从N-1逐渐减少到0。Gi表示在工作过程中部件i的库存量,最大取值为部件i的初始库存量Si。BOi表示部件i的备件短缺数,0≤BOi≤N。根据定义部件i的3个参数,建立部件i的CTMC为{Xi(t)=(Oi(t),Gi(t),BOi(t));t≥0},状态转移图如图1所示。其中包含有Ei=Si+N+1个状态,编号分别为0,1,…,Si+N。图1虚线左侧表示备件充足时部件i的各状态转移过程,虚线右侧表示备件短缺时部件i的各状态转移过程。

图1 部件i的CTMCFig.1 CTMC of component i

当备件i充足时:如果1个部件i出现故障,将使用备件更换故障的部件,此时备件数量减1,可用的装备数仍为N,部件i从状态(N,Si-v,0)转移到相邻状态(N,Si-v-1,0),转移率为NZiλi;当1个部件i被修复后运回备件库中,部件i的备件数增加1,部件i从状态(N,Si-v-1,0)转移到相邻状态(N,Si-v,0),转移率为(v+1)μi。其中,0≤v≤Si-1。

当备件出现短缺时:如果一个部件i出现故障,将造成1个装备暂停运行,即造成可用装备数Oi减少1,备件短缺数BOi增加1,部件i将从状态(N-k,0,k)转移到状态(N-k-1,0,k+1),转移率为(N-k)Ziλi;当1个故障的部件i被修复后,能够使得1个装备恢复正常运行,即可用装备数Oi将增加1,备件短缺数BOi减少1,部件i将从状态(N-k-1,0,k+1)转移到状态(N-k,0,k),转移率为(Si+k+1)μi。其中,1≤k≤N-1。

状态(N,0,0)和状态(N-1,0,1)是连接备件i是否出现短缺的两个状态。分析可知当部件i处于状态(N,0,0)时,如果发生故障,可用装备数Oi将减1,备件短缺数BOi从0变为1,从状态(N,0,0)转移到状态(N-1,0,1)的转移率为NZiλi;当部件i处于状态(N-1,0,1)时,如果1个故障的部件i被修复,将使可用装备数Oi增加1,备件短缺数BOi由1变为0,从状态(N-1,0,1)转移到状态(N,0,0)的转移率为(Si+1)μi。

表1 部件i的状态转移率

2.2 稳态可用度模型

设部件i的瞬时概率分布为pi(t),稳态概率分布为πi,并且满足

(1)

根据CTMC的性质,稳定状态下可以列出方程组

(2)

式中,Ri表示部件i的转移率矩阵;0表示1×Ei维的零矩阵;πi,j表示部件i处于状态j的稳态概率,0≤j≤Si+N。

由图1可以看出各状态之间彼此互通,因此部件i的CTMC是非周期不可约的。由CTMC理论可知[20],方程组(2)存在唯一非负解,因此部件i的各状态存在唯一的稳态概率分布。分析方程组(2)的特点,将状态p(1≤p≤Si+1)的稳态概率表示为

(3)

状态Si+h(2≤h≤N)的稳态概率表示为

πi,Si+h=

(4)

(5)

将式(5)的结果分别代入式(3)和式(4),计算得到部件i的稳态概率矩阵πi。

稳定状态下部件i的期望备件短缺数计算公式为

(6)

式中,EBO(Si,t)是指t时刻部件i的期望备件短缺数;bi是指部件i的备件短缺数向量;bi,m是bi中的元素,指部件i处于状态m时的备件短缺数。bi的具体形式为

bi=[bi,0,bi,1,…,bi,Si+N]T=

(7)

如果某个装备出现备件短缺,该装备即处于不可用状态。故部件i的EBO(Si,t)等价于因备件i短缺造成的不可用装备数的期望值。因此当各装备处于平稳状态时(t→∞),装备群的EBOq等价于因各类备件短缺而造成不可用装备数的期望值之和，即

(8)

装备总数N与稳态下装备群的EBOq相减,得到可用装备数的期望值;而装备群的稳态可用度Aq等价于可用装备数期望值占总装备数N的百分比[19]。因此装备群Aq的计算公式为

(9)

式中,A(t)是指装备群t时刻的瞬时可用度。

如果EBOq≥N,则Aq=0。因为当装备群的EBOq≥N时,表明稳定状态时任何一个装备都不能正常使用,故稳态可用度Aq=0。

2.3 稳态可用度算法

通过第2.1节和第2.2节的分析可知,根据装备群和各类部件的相关信息,分别建立各类部件的CTMC,形成装备群CTMC族模型;然后利用备件短缺数与可用装备数之间的关系,构建装备群稳态可用度模型。算法具体流程图如图2所示,具体步骤如下:

步骤1确定装备群的相关参数。装备总数N、部件类型数L、部件i的故障率λi、维修率μi、部件i的单装备安装数Zi以及部件i初始库存数Si,其中i=1,2,…,L。各部件故障间隔时间以及故障后的维修时间均服从指数分布。

步骤2定义部件i的状态。使用3个参数:受部件i影响的可用装备数Oi、工作过程中部件i的库存量、备件短缺个数,从而确定部件的状态空间。

步骤3建立部件的CTMC。

步骤4确定部件的转移率矩阵。

步骤5求解与部件的CTMC模型相关的方程组,计算部件的稳态概率分布。

步骤6计算部件的期望备件短缺数。

步骤7计算装备群的期望备件短缺数。将每类部件分别执行步骤2～步骤6,联合各类部件的CTMC,构建装备群的CTMC族模型,将各部件的期望备件短缺数进行累加运算,从而计算装备群的期望备件短缺数。

步骤8计算装备群稳态可用度。根据装备群期望备件短缺数与可用度之间的关系,计算装备群稳态可用度。

图2 稳态可用度算法流程图Fig.2 Algorithm flowchart of steady availability

3 案例分析

假设装备群包含5个同型装备,每个装备由4类不同的关键部件串联组成。忽略各类部件故障时的更换时间,并要求装备群连续工作。假设各类部件之间相互独立,部件平均故障间隔时间(mean time between failure,MTBF)、平均维修时间(mean time to repair, MTTR)均服从指数分布,具体数值如表2所示。各类部件的备件库存方案如表3所示。为了验证本文建立的装备群稳态可用度计算模型的有效性,将案例中的数据分别代入本文构建的CTMC族模型(模型1)和多级可修产品库存控制(multi-echelon technique for recoverable item control,METRIC)模型[19](模型2),使用Matlab软件计算装备群稳态可用度;同时使用保障效能仿真软件(SIMLOX)进行仿真检验。3种计算方法的结果如表4所示,绘制的曲线如图3所示。

表2 部件信息

表3 备件库存方案

图3可以看出,在各备件库存方案下，3种模型的稳态可用度曲线几乎重合。随着各类备件数量的增多,装备群稳态可用度逐渐增大并接近于1。对图3中库存方案编号为4、5处进行局部放大,结果显示本文模型的结果同METRIC模型结果十分接近,但前者略微大于后者,更接近SIMLOX仿真的结果。METRIC模型假设装备在工作过程中,对备件的需求量服从泊松分布。在计算备件的EBO时,设定备件短缺数的取值从1到无穷大,而实际装备群中备件短缺数取值是有限的,因此使用METRIC模型计算的EBO会偏高。而本文建立的CTMC族模型中,选取的状态空间确保备件短缺数的取值符合实际情况,因此本文模型计算的备件短缺数要小于METRIC模型的结果。通常情况下,装备群的EBO最小等价于无串件拼修时稳态可用度最大。故本文模型计算的稳态可用度要略微大于METRIC模型的计算结果,更接近于SIMLOX仿真的结果。由此可以看出,本文通过构建CTMC族模型计算装备群稳态可用度的方法是可行且有效的。

表4 不同备件库存方案下稳态可用度的结果

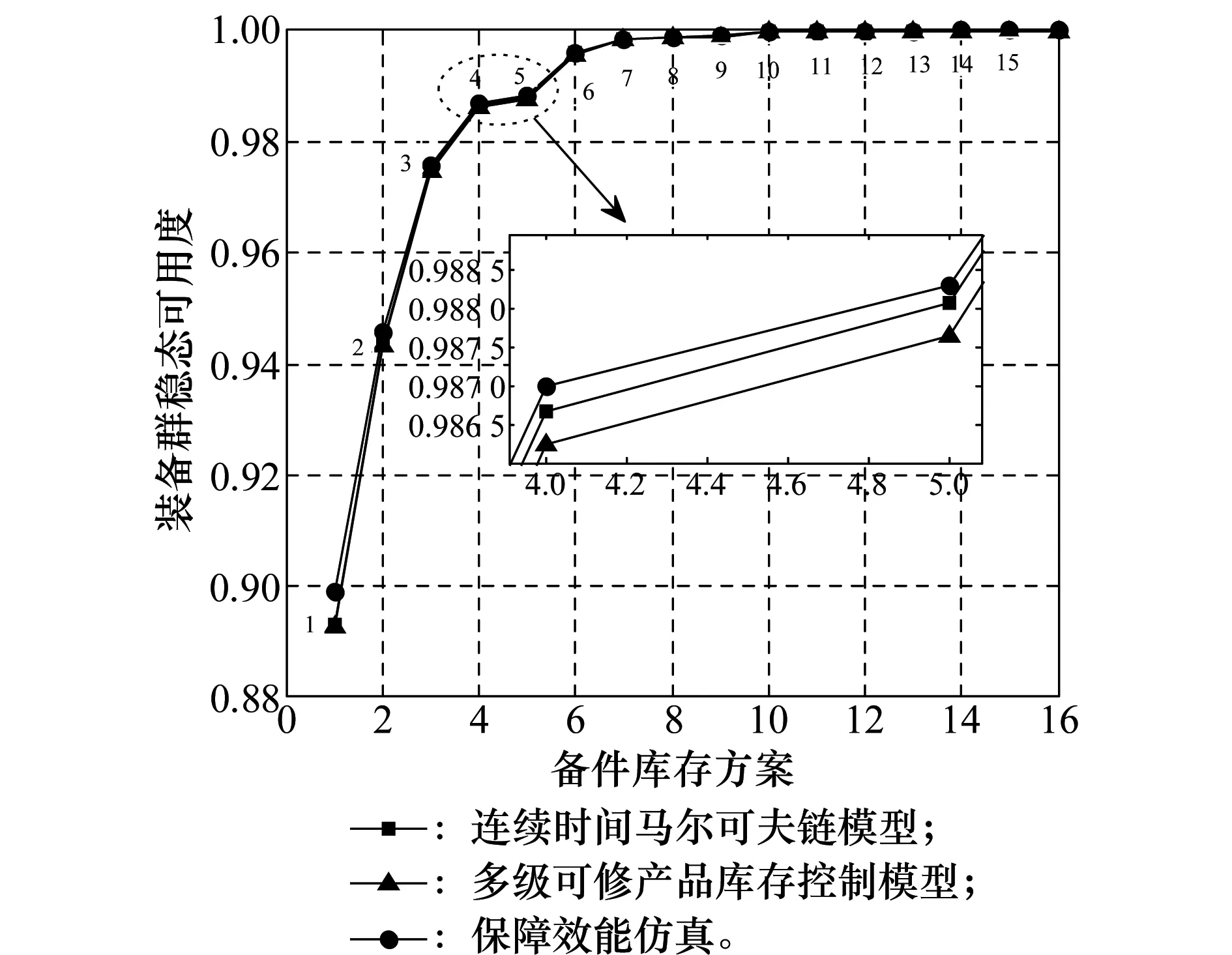
图3 不同备件库存方案下稳态可用度曲线Fig.3 Steady state availability curves under different spare parts inventory schemes

4 结 论

通过本文研究,可以得出如下结论:

(1) 分析了装备群的构型特点,构建了满足库存平衡关系的部件CTMC,并根据部件间的故障逻辑关系建立了装备群CTMC族模型。相对以往利用马尔可夫过程分析装备群可用度的模型而言,这种建模方式能够有效降低装备群CTMC建模空间维数。

(2) 在求解装备群CTMC族稳态概率的基础上,结合各类部件的期望备件短缺数与可用装备数之间的关系,给出了装备群稳态可用度与部件库存状态稳态概率之间的函数关系。

(3) 提出了基于CTMC族的装备群稳态可用度建模的算法流程与框架,为应用CTMC方法计算装备群效能指标提供了一种新的技术途径。

(4) 对本文建立的模型进行仿真实验验证。对比案例结果发现,应用本文模型计算装备群稳态可用度比METRIC模型结果更接近于仿真实验结果。

本文假设对故障件的维修能力无限,但在实际维修中由于一些原因的限制,维修能力往往是有限的。故未来的研究工作会着眼于研究包含维修约束的情况,建立维修能力有限的装备群稳态可用度模型。

参考文献：

[1] 郭小威,李保刚.备件冷储备方案下装备群任务可靠性建模[J].火力与指挥控制,2016,41(1):161-164.

GUO X W, LI B G. Mission reliability modeling of equipment group with cold standby scheme of spare parts[J]. Fire Control & Command Control, 2016, 41(1): 161-164.

[2] 曹晋华, 程侃. 可靠性数学引论[M]. 2版. 北京: 高等教育出版社, 2012: 182-249.

CAO J H, CHENG K. Introduction to mathematical reliability[M]. 2nd ed. Beijing: Higher Education Press, 2012: 182-249.

[3] WOOD A. Availability modeling[J]. IEEE Circuits & Devices Magazine, 1994, 10(3): 22-27.

[4] ZHENG Z, CUI L, HAWKES A G, et al. A study on a single-unit Markov repairable system with repair time omission[J]. IEEE Trans.on Reliability, 2006, 55(2): 182-188.

[5] JIA X J, SHEN J Y, XING R. Reliability analysis for repairable multistate two-unit series systems when repair time can be neglected[J]. IEEE Trans.on Reliability, 2016, 65(1): 208-216.

[6] 印明昂, 孙志礼, 王宇宁, 等. 有备件串联系统的可靠性分析模型[J].东北大学学报(自然科学版),2012,33(10):1461-1464.

YIN M A, SUN Z L, WANG Y N, et al. Reliability model of series system with spare parts[J]. Journal of Northeastern University (Natural Science), 2012, 33(10): 1461-1464.

[7] KHALIL Z S. Availability of series systems with various shut-off rules[J].IEEE Trans.on Reliability,1985,34(2):187-189.

[8] 耿岩, 郭霖瀚, 王寄明, 等. 考虑休眠的两部件系统可用度马氏建模方法[J]. 仪器仪表学报, 2016, 37(9): 1996-2003.

GENG Y, GUO L H, WANG J M, et al. Markov modeling method for availability of two-item system under passivation[J]. Chinese Journal of Scientific Instrument,2016,37(9):1996-2003.

[9] 李红霞, 孟宪云, 李宁. 可忽略部分维修时间的串联可修系统的可用度分析[J]. 燕山大学学报, 2007, 31(6): 542-544.

LI H X, MENG X Y, LI N. An availability analysis of series repairable system with repair omission[J]. Journal of Yanshan University, 2007, 31(6): 542-544.

[10] KUO C, SHEU S, KE J, et al. Reliability-based measures for a retrial system with mixed standby components[J]. Applied Mathematical Modelling, 2014, 38(19): 4640-4651.

[11] HU L M, YUE D Q, LI J D. Probabilistic analysis of a series-parallel repairable system with three units and vacation[J]. Applied Mathematical Modelling, 2010, 34(10): 2711-2721.

[12] FROSTIG E, LEVIKSON B. On the availability of R out of N repairable systems[J]. Naval Research Logistics (NRL), 2002, 49(5): 483-498.

[13] MOGHADDASS R, ZUO M J, QU J. Reliability and availability analysis of a repairable k-out-of-n: G system with R repairmen subject to shut-off rules[J]. IEEE Trans.on Reliability, 2011, 60(3): 658-666.

[14] XIE W, LIAO H T, JIN T D. Maximizing system availability through joint decision on component redundancy and spares inventory[J]. European Journal of Operational Research, 2014, 237(1): 164-176.

[15] CEKYAY B, OZEKICI S. Reliability, MTTF and steady-state availability analysis of systems with exponential lifetimes[J]. Applied Mathematical Modelling, 2015, 39(1): 284-296.

[16] WU W, TANG Y, YU M, et al. Reliability analysis of a k-out-of-n: G repairable system with single vacation[J]. Applied Mathematical Modelling, 2014, 38(24): 6075-6097.

[17] SMIDT-DESTOMBES K S D, HEIJDEN M C V D, HARTEN A V. On the availability of a k-out-of-N, system given limited spares and repair capacity under a condition based maintenance strategy[J]. Reliability Engineering & System Safety, 2004, 83(3): 287-300.

[18] ANGUS J E. Availability of continuous service and computing long-run MTBF and reliability for Markov systems[J]. Probability in the Engineering and Informational Sciences,2001,15(3): 369-381.

[19] SHERBROOKE C C. Optimal inventory modeling of systems: multi-echelon techniques[M]. 2nd ed. Boston: Springer Science & Business Media, 2006: 37-40.

[20] KULKARNI V G. Modeling and analysis of stochastic systems[M]. 2nd ed. Boca Raton: CRC Press, 2009: 231-232.