认知网络中基于三角分解的干扰对齐算法

李兆玉, 马东亚, 唐 宏, 徐 栋

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065;2. 移动通信技术重庆市重点实验室, 重庆 400065)

0 引 言

无线通信业务的飞速发展使得原本就稀缺的频谱资源更加的供不应求。认知无线电技术能够使认知用户(次用户)利用授权用户(主用户)的频谱空洞,而达到提高频谱利用率的效果[1]，但次用户被允许接入的前提是其不会对主用户的通信质量造成不利的影响。因此,干扰成为认知系统中较为核心的问题。近期,干扰对齐作为一种有效处理干扰的方法被用到认知无线网络中[2]。

文献[3-4]提出干扰对齐的核心思想是用户间通过联合预编码设计在接收端将来自其他用户的干扰信号对齐到尽量小的空间中,而使期望信号获得更多的信号空间。在文献[5-6]中证明了干扰对齐成立的必要条件。在认知网络中运用干扰对齐技术进行干扰消除,可以有效利用系统的空域资源,使得次用户在不影响主用户通信的情况下,同时同频地接入[7-9]。文献[10]中在时分双工的模式下利用信道互易性,将正反向链路迭代式的干扰对齐方法,运用在认知多输入多输出(multiple-input multiple-output,MIMO)网络中。在文献[11]中,由于主用户为提高系统容量对信道进行注水功率分配,如此以来,次用户可以使用主用户未使用的信号空间,且不会影响主用户的通信,但该算法却没有考虑主用户对次用户造成的干扰。文献[12-13]对认知无线网络中干扰对齐成立的必要条件及其自由度上限进行了分析,并验证了所得结论的正确性。在文献[14-16]中由次用户单方面消除主次间的干扰,但却带来次用户性能严重损失的问题。如果主用户和次用户能够相互知道对方的信道状态信息,那么主用户和次用户间可以进行协作处理干扰[17-18],文献[17]在一个主用户、多个次用户的系统模型下,为解决由次用户系统消除主次用户间干扰,带来次用户性能严重损失的问题。由主用户系统负责处理次用户对主用户的干扰,虽然该算法一定程度上解决了次用户的性能不佳的问题,但却违背了不影响主用户通信质量的初衷。文献[18]考虑多个主用户、多个次用户的系统模型,通过主用户和次用户相互协作的干扰对齐,提高了次用户自由度上限,进而提高次用户性能,但同样会牺牲主用户的性能。

基于上述分析,在认知MIMO网络中,不同于由次用户单方面消除主次间干扰的传统算法和主次协作认知干扰对齐算法[17-18],本文首先根据各用户信道质量的差异,分别对主用户系统和次用户系统的信道矩阵进行调整排序,然后,联合主次用户系统进行三角分解,如此以来,使得信道质量越好的主用户受到其他主用户的干扰个数越少、信道越好的次用户受到其他次用户的干扰个数越少,并且同时消除了一半的次用户间和主用户对次用户以及一半的主用户间的干扰。最后还分析了本文算法下次用户自由度上限,并通过最小均方误差算法验证其正确性和合理性。仿真实验表明,本文算法能够有效地改善主用户和次用户系统的性能。

1 系统模型

本文考虑如图1所示的认知MIMO系统。该系统共有K(K=Kp+Ks)对用户,其中Kp、Ks分别表示主用户对数和次用户对数,且每个主用户对的发端配有天线Mp根、收端配有天线Np根,每个次用户对的发收两端分别配有Ms和Ns根天线,并且用户i(i=1,2,…,K)发送di个数据流(即用户i的自由度为di)。

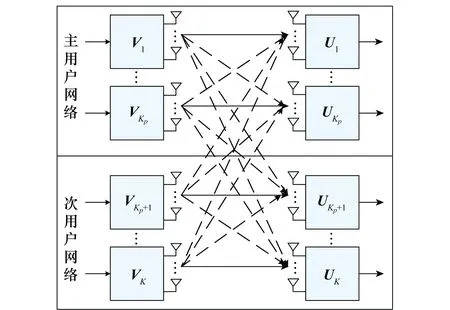
图1 认知MIMO网络系统模型Fig.1 Cognitive MIMO network system model

在特定的时频资源上,接收机i的接收信号为

(1)

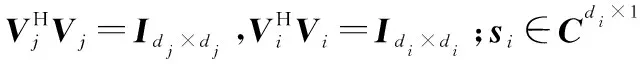
2 信道矩阵排序及三角分解

针对图1所示的系统模型,由于系统中各用户的信道质量有相对的好坏之分,因此在进行联合主次用户信道矩阵进行三角分解之前,首先根据信道质量分别对主用户网络和次用户网络的信道矩阵进行调整,而信道矩阵的迹可以表示其好坏,且信道矩阵的迹越大表示信道质量越好。由矩阵理论[19]可知,信道矩阵的迹表示为

(2)

式中,k=1,2,…,K。按照信道矩阵的迹的大小分别对主用户系统和次用户系统进行排序

ttr,1≤ttr,2≤ttr,3…≤ttr,Kp

(3)

ttr,Kp+1≤ttr,Kp+2≤ttr,Kp+3…≤ttr,K

(4)

如此以来,在进行三角分解之后,使得信道越好的主用户受到其他主用户的干扰个数越少、信道越好的次用户受到其他次用户的干扰个数越少。

经过调整排序后,整个系统的信道矩阵表示为

(5)

用向量的方式表示接收端所接收到的信号

(6)

式中,Hpp、Hsp、Hps、Hss分别表示主用户之间、主用户到次用户、次用户到主用户以及次用户之间的发端到收端的信道矩阵;Vp和Vs分别表示主用户系统的预编码矩阵和次用户系统的预编码矩阵。

对整个系统联合主次用户信道矩阵H进行三角分解

(7)

式中,Q∈CKN×KN为酉矩阵;L∈CKN×KM为上三角矩阵。根据矩阵理论分析可得矩阵L和矩阵H有相同的统计特性,因此可用矩阵L等效为主次联合的信道矩阵。此时式(6)可表示为

(8)

由式(7)可知经过三角分解后Lpp等于

为联合主次信道系统进行三角分解后主用户发射机到主用户接收机之间的信道矩阵,因为经分解后矩阵Lpp左下部分均为0,而该部分为一半的主用户之间的干扰信道矩阵。因此,Lpp为一半的主用户之间干扰链路被消除后的信道矩阵;Lss等于

为联合主次信道系统进行三角分解后次用户发射机到次用户接收机之间的信道矩阵,因为经分解后Lss左下部分均为0,而该部分为一半的次用户之间的干扰信道矩阵。因此,Lss为一半的次用户间的干扰链路被消除后的信道矩阵;Lps等于

为联合主次信道系统进行三角分解后次用户到主用户之间的信道矩阵。因此,对整个系统联合主次用户信道矩阵H进行三角分解,使得同时消除了一半的次用户间和主用户对次用户以及一半的主用户间的干扰。

对式(8)等式两边进行左乘Q-1的预处理得:

(9)

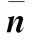
接收机在经过干扰抑制矩阵U∈CN×d处理之后为

(10)

式中,N为接收机天线个数；d为数据流的个数；Up和Us分别表示为所有主用户和所有次用户的干扰抑制矩阵所构成的总干扰抑制矩阵。

3 次用户自由度分析

定理1在上述联合主次信道矩阵进行三角分解的认知MIMO网络中,次用户网络干扰对齐可行的必要条件为

(11)

证明不同于传统认知干扰对齐算法,由次用户系统消除次用户对主用户以及主用户对次用户的干扰,本文算法因为联合了主次用户信道矩阵进行三角分解消除了主用户对次用户的干扰,因此次用户仅需进行编码消除次用户对主用户的干扰。此时,次用户干扰对齐的可行性条件需满足如下3个等式:

(12)

(13)

(14)

式(12)表示由次用户系统消除次用户对主用户的干扰;式(13)表示次用户系统消除次用户之间的干扰;式(14)表示每一个次用户的收端都能恢复出所期望的信号,且式(12)、式(13)有解,则式(14)必然成立[6]。

要使次用户线性干扰对齐成立需使式(12)、式(13)同时成立,即方程组有解。由Bezout定理,如果式(12)、式(13)所组成的方程组中独立变量的个数(Nv)大于等于方程个数(Ne),则该方程组有解。而在计算独立变量个数Nv时,应忽略无助于干扰对齐的变量。因此,通过矩阵的行变换[6]得

(15)

(16)

由于联合了主次用户信道进行三角分解,已经消除了主用户对次用户的干扰,所以本文算法下独立方程组与传统认知MIMO干扰对齐算法下相比,少了消除次用户受到主用户的干扰的方程,此时,根据式(12)、式(13)得独立方程个数为

(17)

考虑每个次用户的自由度均为ds,每个主用户的自由度均为dp,由Nv≥Ne得

(18)

证毕

定理2在根据上述联合主次信道矩阵进行三角分解的认知MIMO网络中,假设每个次用户和每个主用的自由度均分别为ds、dp,则每一个次用户的自由度上限为

(19)

证明式(19)包含了两类不等式约束:

(1)第一类是在任意一个次用户对、Kp个主用户对所构成的网络中,主用户部分共有Kpdp个数据流,由于利用三角分解次用户受到主用户的干扰已经被消除,可得

ds+Kpdp≤min{Ms+Kpdp,

Ns+Kpdp,max(Kpdp,Ms)}

(20)

又有

Ms+Kpdp≥max(Kpdp,Ms)

(21)

则有

ds+Kpdp≤min{Ns+Kpdp,max(Kpdp,Ms)}

(22)

则此时次用户自由度上限为

ds≤min{Ns,Ms-Kpdp}

(23)

(2)第二类是任意两个次用户对组成的干扰网络也需要满足MIMO干扰网络的自由度分析[4]方法,经过三角分解消除一半的次用户间的干扰,可以得到

2ds≤min{2Ms,2Ns,max(Ms,Ns)}

(24)

化简得

(25)

结合第一类和第二类结果可得

(26)

由定理1和定理2可得,由Ks对次用户和Kp对主用户所组成的认知MIMO网络中,每一个次用户的自由度上界为

(27)

证毕

4 次用户干扰对齐算法

4.1 主用户对次用户干扰的消除

因为次用户被允许接入的前提是其不会对主用户的通信质量造成不利的影响,因此,在求解最优的次用户的预编码和干扰抑制矩阵时,不但要考虑次用户间的干扰,而且还要考虑主次用户间干扰。由于上文中通过结合主用户网络和次用户网络进行了三角分解,主用户对次用户的干扰已经被消除,而对于次用户对主用户的干扰的消除方法,可根据矩阵理论对Vi进行分解:

(28)

用Bi来消除所有次用户对主用户i所产生的干扰，其表达式如下:

(29)

式中,∀i=Kp+1,Kp+2,…,K;j=1,2,…,Kp。

令

(30)

式(29)成立,则Bi取Oi的零空间,且维数为

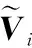
当消除了主次用户间的干扰,主用户之间和次用户之间的干扰问题均可以转化为标准的干扰对齐模型,为方便分析,次用户网络的信道可以等效为

(31)

式中,∀i,j=Kp+1,Kp+2,…,K。

4.2 干扰对齐算法描述

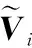
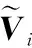
(32)

经过矩阵运算得

(33)

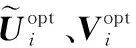
(34)

由KKT条件

(35)

由矩阵乘积的迹的梯度性质[19]:

(36)

(37)

(38)

(39)

(40)

对f求Ui的偏导:

(41)

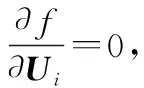
(42)

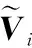
(43)

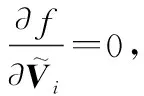
(44)

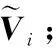
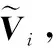
步骤4重复步骤2和步骤3直到收敛。

4.3 算法收敛性分析

由于以最小均方误差准则进行干扰对齐,迭代步骤2到步骤3均以最小化均方误差的值为优化目标,且每次的优化均在上一次迭代结果的基础上进一步压缩干扰信号空间和提高信干噪比,因此,每一次迭代后均会产生单调递减的序列。又因为以最小均方误差为目标的函数是有界的,因此根据单调有界理论,算法是收敛的。

在本文第5节仿真结果与分析部分中,根据干扰泄漏在期望信号子空间的功率随迭代次数变化的仿真图,可以进一步验证算法的收敛性。

5 仿真结果与分析

将本文算法与主次协作干扰对齐算法[18]、传统认知干扰对齐算法[14]、文献[20]算法和文献[21]算法进行对比,来验证其有效性。不失一般性,设所有信道满足平坦衰落,各元素相互独立且满足均值为0方差为1的复高斯分布;系统中每个数据流的发射功率相同;系统中无论是主用户还是次用户,无论是发端还是收端均配有相同的天线数,即Mp=Np=Ms=Ns=M。需要强调的是,因为文献[20]的算法、文献[21]的算法与本文对比的另一种传统认知干扰对齐算法均是由次用户单方面消除主次用户间的干扰,而主用户间均用的是最小干扰泄漏算法进行干扰对齐。因此,这3种算法的主用户系统的性能是一样的,在后续仿真中涉及到主用户性能对比图中均只仿真了传统认知干扰对齐算法的主用户性能作为代表。

图2表示5种算法在Kp=Ks=3,且每个主用户自由度dp=2时,系统总的自由度上限随天线数M变化的曲线图。结果表明本文算法和主次协作干扰对齐算法的系统总自由度,随着天线数的增加始终优于传统认知干扰对齐算法,并且本文算法的系统总的自由度上限大于等于主次协作干扰对齐算法的系统总的自由度上限,原因是本文算法对整个系统矩阵进行三角分解,同时消除了一半的次用户间和主用户对次用户的干扰,相比与传统算法相当于节省了天线数,而主次协作干扰对齐算法主用户以牺牲自己的性能为代价,补偿了次用户为消除主次间干扰而带来的损失,虽然相比于传统算法自由度也有所提高,但并没有本文算法效果好,而文献[20]的算法、文献[21]的算法和传统认知干扰对齐算法一样均由次用户单方面进行消除主次间的干扰。因此,三者的系统自由度值相同。

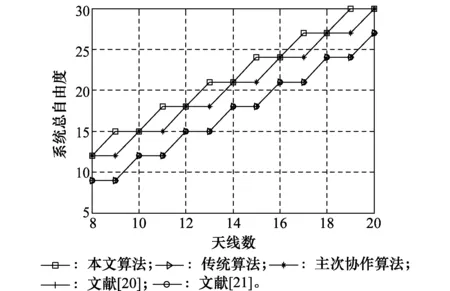
图2 系统总自由度上限分析Fig.2 System total degree of freedom analysis

图3表示5种算法在Kp=Ks=3,dp=ds=2,主次用户收发天线数M=13时,系统和容量随信噪比变化的曲线图,从仿真结果可知,对比次用户系统的和容量,本文算法经过联合主次用户信道进行三角分解,次用户仅需要损失一部分性能去消除次用户对主用户的干扰,而不需要再牺牲自己的性能去消除来自主用户的干扰;基于主次协作的干扰对齐算法中,次用户牺牲自身的性能去消除主用户对次用户的干扰,并且与主用户进行协作消除主用户对次用户的干扰,虽减少了次用户性能的损失但次用户仍然需要损失自己的性能;传统的认知干扰对齐算法需要次用户单方面的消除主用户对次用户和次用户对主用户的干扰;文献[20]所提算法,在传统认知干扰对齐算法的基础上进行改进,虽明显的加快了收敛速度,但和容量并没有明显增加;文献[21]所提算法,虽然仍需要损失较多的性能消除主次间的干扰,尤其是当主用户所发的数据流和用户数都比较多的时候,但其次用户接入机制以及目标函数的选取更优,其和容量好于基于主次协作的干扰对齐算法。因此,本文算法下的次用户容量最优,基于传统认知干扰对齐算法的最差。对比主用户系统和容量,所提算法相较于传统算法,由于经过三角分解消除了一半的主用户间的干扰,因此性能得到提升;而主次协作干扰对齐算法相较于传统算法主用户为提高次用户性能,带来了自身性能的损失。因此,本文算法下的主用户和容量最优,而基于主次协作干扰对齐算法的主用户和容量最差。

图3 和容量分析Fig.3 Sum capacity analysis

图4表示5种算法在Kp=Ks=3,dp=2,主次用户收发天线数M=13时,干扰在有用信号空间的功率百分比随系统总自由度的变化曲线图,功率百分比定义为

∀k=Kp+1,…,K

(45)

式中,Qk为干扰协方差矩阵;λi(A)表示矩阵A的第i个最小的特征值。从仿真结果可知,由于当系统总自由度大于15时,传统认知干扰对齐算法、文献[20]的算法和文献[21]的算法的干扰功率百分比明显大于0,因此这3种算法的干扰对齐是不可实现的。同理,当系统总自由度大于18时,主次协作干扰对齐算法是不能实现的;而本文算法是在系统总自由度大于21时干扰对齐不能实现。此结果与前文自由度上限分析的结果一致。

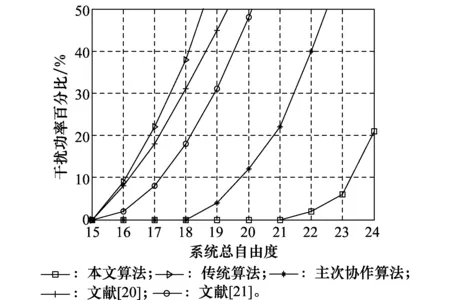
图4 干扰功率百分比分析Fig.4 Interference power percentage analysis

图5表示5种算法在Kp=Ks=3,dp=ds=2,主次用户收发天线数M=13时,平均能量效率关于信噪比的变化,其中平均能量效率表示为log2(Idi+SINRi)/Pi,单位为bit/(Hz·J),其中Pi表示为第i个用户的发射功率。从仿真结果可知,对比次用户能量效率,本文算法相比较于主次协作干扰对齐算法、文献[20]的算法、文献[21]的算法和传统认知干扰对齐算法均有较大的提高。对比主用户能量效率,本文算法较于其他两种算法也有较大的提高。

图5 能量效率分析Fig.5 Energy efficiency analysis

图6表示为5种算法在Kp=Ks=3,dp=ds=2,主次用户收发天线数M=13,且每个用户的发射功率均为25 dB时,主用户系统中干扰泄漏在期望信号子空间的功率和次用户系统中干扰泄漏在期望信号子空间的功率,随迭代次数变化的曲线图。而该功率的大小可以一定程度上反映干扰对齐的质量。仿真结果可知,随着迭代次数的增加,次用户系统中,干扰对齐效果从好到坏依次是本文算法干扰对齐、文献[21]的算法、文献[20]的算法、主次协作干扰对齐算法和传统认知干扰对齐算法。主用户系统中,主次协作干扰对齐算法的干扰对齐效果差于传统认知干扰对齐算法,其原因是由于主次协作干扰对齐算法中为提升次用户性能做出了牺牲。而本文算法仍是最优的。

图6 干扰泄漏在信号子空间功率分析Fig.6 Interference leakage in signal subspace power analysis

6 结 论

本文在多个主用户和多个次用户的认知MIMO网络中,充分考虑了主次用户之间的干扰。首先,通过联合主次用户网络的信道矩阵根据信道质量的好坏进行调整排序。然后,进行三角分解,使得信道越好的主用户受到其他主用户的干扰个数越少、信道越好的次用户受到其他次用户的干扰个数越少,并且同时消除了一半的次用户间和主用户对次用户以及一半的主用户间的干扰。最后,推导出该算法下系统总的自由度上限,并通过最小均方误差算法来验证了所提算法的可行性。仿真结果表明,所提算法有效地提高了次用户的自由度上限以及主用户网络和次用户网络的性能。

参考文献：

[1] HAYKIN S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220.

[2] GOMADAM K, CADAMBE V R, JAFAR S A. A distributed numerical approach to interference alignment and applications to wireless interference networks[J]. IEEE Trans.on Information Theory, 2011, 57(6): 3309-3322.

[3] CADAMBE V R, JAFAR S A. Interference alignment and degrees of freedom of the-user interference channel[J]. IEEE Trans.on Information Theory, 2008, 54(8): 3425-3441.

[4] JAFAR S A, FAKHEREDDIN M J. Degrees of freedom for the MIMO interference channel[J]. IEEE Trans.on Information Theory, 2007, 53(7): 2637-2642.

[5] RUAN L, LAU V K N, WIN M Z. The feasibility conditions for interference alignment in MIMO networks[J]. IEEE Trans.on Signal Processing, 2013, 61(8): 2066-2077.

[6] YETIS C M, GOU T, JAFAR S A, et al. On feasibility of interference alignment in MIMO interference networks[J]. IEEE Trans.on Signal Processing, 2010, 58(9): 4771-4782.

[7] MEN H, ZHAO N, JIN M, et al. Optimal transceiver design for interference alignment based cognitive radio networks[J]. IEEE Communications Letters, 2015, 19(8): 1442-1445.

[8] GARG S, JAIN M, GANGOPADHYAY R, et al. Opportunistic interference alignment in multi-user MIMO cognitive radio networks for different fading channels[C]∥Proc.of the 22nd IEEE National Conference on Communication, 2016: 1-6.

[9] MEI R. Rayleigh quotient based interference alignment spectrum sharing in MIMO cognitive radio networks[J]. China Communications, 2015, 12(6): 96-105.

[10] XU Y, MAO S. Distributed interference alignment in cognitive radio networks[C]∥Proc.of the 22nd IEEE International Conference on Computer Communication and Networks,2013:1-7.

[11] PERLAZA S M, FAWAZ N, LASAULCE S, et al. From spectrum pooling to space pooling: opportunistic interference alignment in MIMO cognitive networks[J]. IEEE Trans.on Signal Processing, 2010, 58(7): 3728-3741.

[12] 孙献, 赵晓晖. 认知无线电系统中干扰对齐的自由度分析[J]. 通信学报, 2016, 37(2): 179-189.

SUN X, ZHAO X H. Cognitive radio system interference alignment of the degree of freedom analysis[J]. Journal of Communications, 2016, 37(2): 179-189.

[13] AMIR M, EL-KEYI A, NAFIE M. Constrained interference alignment and the spatial degrees of freedom of MIMO cognitive networks[J].IEEE Trans.on Information Theory,2011,57(5): 2994-3004.

[14] XU T, MA L, STERNBERG G. Practical interference alignment and cancellation for MIMO underlay cognitive radio networks with multiple secondary users[C]∥Proc.of the IEEE Global Communications Conference, 2013: 1009-1014.

[15] LI N, WANG S, ZHAI L. A robust interference alignment algorithm in a MIMO interference channel[C]∥Proc.of the 16th IEEE International Symposium on Communications and Information Technologies, 2016: 500-504.

[16] NAURYZBAYEV G, KALIYEVA S. Interference alignment cancellation scheme for network-mimo systems[C]∥Proc.of the IEEE International Conference on Information and Communication Technology Convergence, 2016: 237-240.

[17] KOO B, PARK D. Interference alignment with cooperative primary receiver in cognitive networks[J]. IEEE Communications Letters, 2012, 16(7): 1072-1075.

[18] 李世党. 面向B4G/5G无线网络的干扰对齐与干扰管理技术研究[D]. 南京: 东南大学, 2016.

LI S D. Research on interference alignment and interference management technology for B4G / 5G wireless network[D]. Nanjing: Southeast University, 2016.

[19] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004: 44-46.

ZHANG X D. Matrix analysis and application[M]. Beijing: Tsinghua University Press, 2004.

[20] REZAEI F, TADAION A. Interference alignment in cognitive radio networks[J]. IET Communications,2014,8(10):1769-1777.

[21] REZAEI F, TADAION A. Sum-rate improvement in cognitive radio through interference alignment[J]. IEEE Trans.on Vehicular Technology, 2016, 65(1): 145-154.