平方根递推更新GMP-PHDF

梁志兵, 刘付显, 高嘉乐

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

多目标跟踪(multi-target tracking,MTT)的目的是在每一时刻,从存在漏检、虚警和数据关联不确定的量测集中,联合估计目标状态及数目。传统的MTT方法,如联合概率数据关联[1](joint probabilistic data association,JPDA)和多假设跟踪[2-3](multiple hypothesis tracking,MHT),由于考虑目标与量测之间复杂的数据关联,在计算上难以实现。近年来,基于随机有限集的MTT方法受到广泛关注。其中,概率假设密度滤波器[4](probability hypothesis density filter,PHDF)是一种有效的贝叶斯MTT方法,其能够避免数据关联难题,实现目标状态及数目的快速估计。

目前,PHDF主要有序贯蒙特卡罗(sequential Monte Carlo, SMC)PHDF[5-6](SMC-PHDF)和高斯混合(Gaussian mixture,GM)PHDF[7](GM-PHDF)两种实现技术。SMC-PHDF能够处理非线性非高斯情况下的MTT问题,但其需要重采样和粒子聚类[5],且聚类技术容易导致目标状态及数目的不正确估计。而GM-PHDF可得到PHDF的闭式解,且高斯量的均值代表目标状态,状态估计较为准确且计算量较小,但其只适用于线性高斯场景。对于非线性场景,文献[7]提出扩展卡尔曼(extended Kalman,EK)PHDF和无迹卡尔曼(unscented Kalman,UK)PHDF,但在强非线性模型下,二者均会出现滤波发散问题[8]。对此,Clark等[9]提出GMP-PHDF,其结合蒙特卡罗方法和高斯混合实现技术的优势,不需要聚类技术和重采样,可有效处理强非线性模型下的MTT问题。

但现有的GMP-PHDF均采用状态转移概率密度作为重要性密度函数,当量测处于其尾部或量测精度较高时,会出现粒子退化现象。而最优重要性密度函数应与当前测量值条件相关,形状接近真实后验分布[10]。事实上,近年来出现很多针对重要性密度函数选取的粒子滤波改进方法,如扩展卡尔曼粒子滤波(extended Kalman filter, EKF)[11],无迹卡尔曼粒子滤波(unscented Kalman filter,UKF)[12],容积粒子滤波[13]等,这些方法均利用非线性滤波方法结合最新测量值得到重要性密度函数,可使状态转移概率密度朝着高似然区域移动,从而提高滤波精度。但是,这些方法本质上均基于卡尔曼滤波框架,而卡尔曼滤波仅在线性最小方差准则下是最优的,这使得上述非线性滤波方法并不能准确得到后验概率密度[14-15]。文献[15]提出一种基于EKF的递推更新方法,依据测量函数的梯度递推式地进行状态更新,可有效克服卡尔曼滤波框架的限制,实现量测对状态的非线性更新,但EKF的线性化计算使其状态估计并不准确。对此,文献[16]将递推更新方法推广应用于非线性高斯滤波中,得到递推更新高斯滤波器(recursive update Gaussian filter,RUGF),并利用其为高斯粒子滤波选择重要性密度函数,可获得更加接近于真实分布的状态后验估计。但在递推过程中,利用数值方法(如UKF，容积卡尔曼滤波(cubature Kalman filter,CKF)等)近似高斯积分时,由于计算误差及噪声的影响,极易出现协方差矩阵非正定的情况,而导致递推过程中断。

为了提高GMP-PHDF的滤波精度,本文首先分析(平方根RUGF(square-root RUGF),SR-RUGF)的实现思路,并给出基于CKF的SR-RUGF实现步骤,避免了协方差矩阵非正定引起递推中断的问题;其次,利用SR-RUGF为GMP-PHDF选取重要性密度函数,从而得到基于平方根递推更新的GMP-PHDF改进算法。

本文首先给出GMP-PHDF的算法流程;其次,给出RUGF的实现步骤,在此基础上分析SR-RUGF的实现思路,并给出基于CKF的SR-RUGF实现步骤;最后提出平方根递推更新GMP-PHDF(square-root recursive update GMP-PHDF,SRRU-GMP-PHDF)滤波算法,并对SR-RUGF的算法复杂度进行分析。仿真实验表明,SRRU-GMP-PHDF算法可以很好地利用量测信息,获得更高精度的估计结果。

1 高斯混合粒子概率假设密度滤波

GMP-PHDF有效结合GM-PHDF和蒙特卡罗方法的优势,其PHD由一组高斯量的和近似,目标状态和数目可通过各高斯量及其权值获得,不需要重采样和聚类技术,但其可处理动态方程和测量方程均为非线性的MTT问题。

设定非线性高斯动态模型和测量模型为

fk+1|k(x|ξ)=N(x;φk(ξ),Qk)

(1)

gk+1(z|x)=N(z;hk+1(x),Rk+1)

(2)

式中,N(·;m,P)表示均值为m,方差为P的高斯分布;φk和hk+1分别表示非线性状态转移函数和测量函数;Qk和Rk+1分别为过程噪声协方差和测量噪声协方差。

假设k时刻目标PHD和k+1时刻新生目标PHD为高斯混合形式:

(3)

(4)

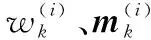
(1) 预测

首先,将目标PHDvk、状态转移密度fk+1|k及新生目标PHDγk+1代入PHD预测方程[4](这里不考虑目标衍生问题),可得

vk+1|k(x)=

(5)

进一步递推得

vk+1|k(x)=

(6)

(7)

(8)

(9)

由此可以得到预测PHD:

vk+1|k(x)=

(10)

(2) 更新

假设k+1时刻的预测PHD为

(11)

将其与测量密度gk+1代入PHD更新方程[4],得

vk+1(x)=(1-PD,k+1)vk+1|k(x)+

(12)

式中

(13)

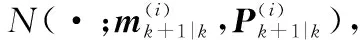
(14)

对此,k+1时刻更新PHD可表示为

vk+1(x)=(1-PD,k+1)vk+1|k(x)+

(15)

式中

(16)

(17)

(18)

2 基于递推更新的GMP-PHDF

2.1 递推更新高斯滤波器[16]

RUGF依据测量函数的梯度递推式地进行状态更新,可有效克服卡尔曼滤波框架的限制并很好地利用量测信息,实现量测对状态的非线性更新。

首先定义

(19)

(20)

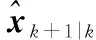
其中,N为递推次数,R为测量噪声协方差。高斯积分可利用多种数值计算方法,如UKF,CKF等进行求解。从表1可看出,递推更新过程可以视作为将当前量测按照递推次数分为N等份,每次对状态进行渐进式的更新。

2.2 平方根递推更新高斯滤波器

通过分析表1的实现步骤可以发现,RUGF本质是:①xk+1、zk+1与测量噪声之间的协方差,即Ck+1和Dk+1均不假设为0,参与递推更新过程;②利用量测对状态进行渐进式的更新。

表2 CKF-SR-RUGF实现步骤

其中,m=2nx,nx为状态向量的维数,且Vk+1为测量噪声。chol(A)返回矩阵A的Cholesky上三角矩阵;qr{A}表示先对矩阵AT求QR分解得到矩阵Q′和R′,然后只返回矩阵R′的上三角部分的转置矩阵。另外,ηj为CKF容积点,其表达式为

(21)

式中,[1]j表示容积点集中的第j个元素,以n=4为例,容积点集可表示为

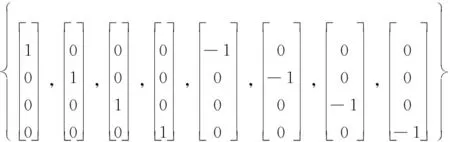
2.3 平方根递推更新GMP-PHDF

最优的重要性密度函数应与当前测量值条件相关,形状接近真实后验分布。递推更新可以更好地利用量测信息,获得的状态后验估计更为接近真实分布,而其平方根实现又可有效解决因协方差矩阵非正定而引起的递推中断问题。对此,本文利用SR-RUGF为GMP-PHDF产生重要性密度函数,得到SRRU-GMP-PHDF算法,具体实现如表3所示。

表3 SRRU-GMP-PHDF实现步骤

3 SR-RUGF复杂度分析

一个算法的复杂度分析对其工程实用至关重要。对此,以容积求积准则为例,利用CKF、CKF-RUGF和CKF-SR-RUGF选取重要性密度函数,这里对它们的计算复杂度进行分析比较。CKF-SR-RUGF的单次计算量分析如表4所示。

其中,i表示递推更新的次数,m为量测维数,且n为状态维数。对于维数为l×p的矩阵,QR分解的计算量为2lp2,Cholesky分解的计算量为lp2+p3/3。

根据文献[20],CKF选取重要性密度函数的计算量为

m3+3m2+2mn+m

(22)

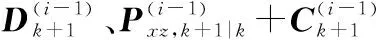
m3+4m2+4mn+m)

(23)

根据表4,本文CKF-SR-RUGF的计算量为

3m3+12n2m+6m2n-m2+12mn+m)

(24)

从上述分析不难看出,单次CKF-RUGF的计算量略大于CKF的计算量,而由于QR分解的引入,CKF-SR-RUGF的计算量要大于CKF- RUGF的计算量。但相对于CKF,CKF-SR-RUGF计算量的增加主要还是来自于递推次数N。因此,在实际应用中,应选择合适的N以权衡计算复杂度和所需精度。

4 仿真分析

假设传感器的测量范围是半径为2 000 m的半圆,共存在6个目标,它们具体进入和离开测量区域的时间以及真实的运动轨迹如图1所示。

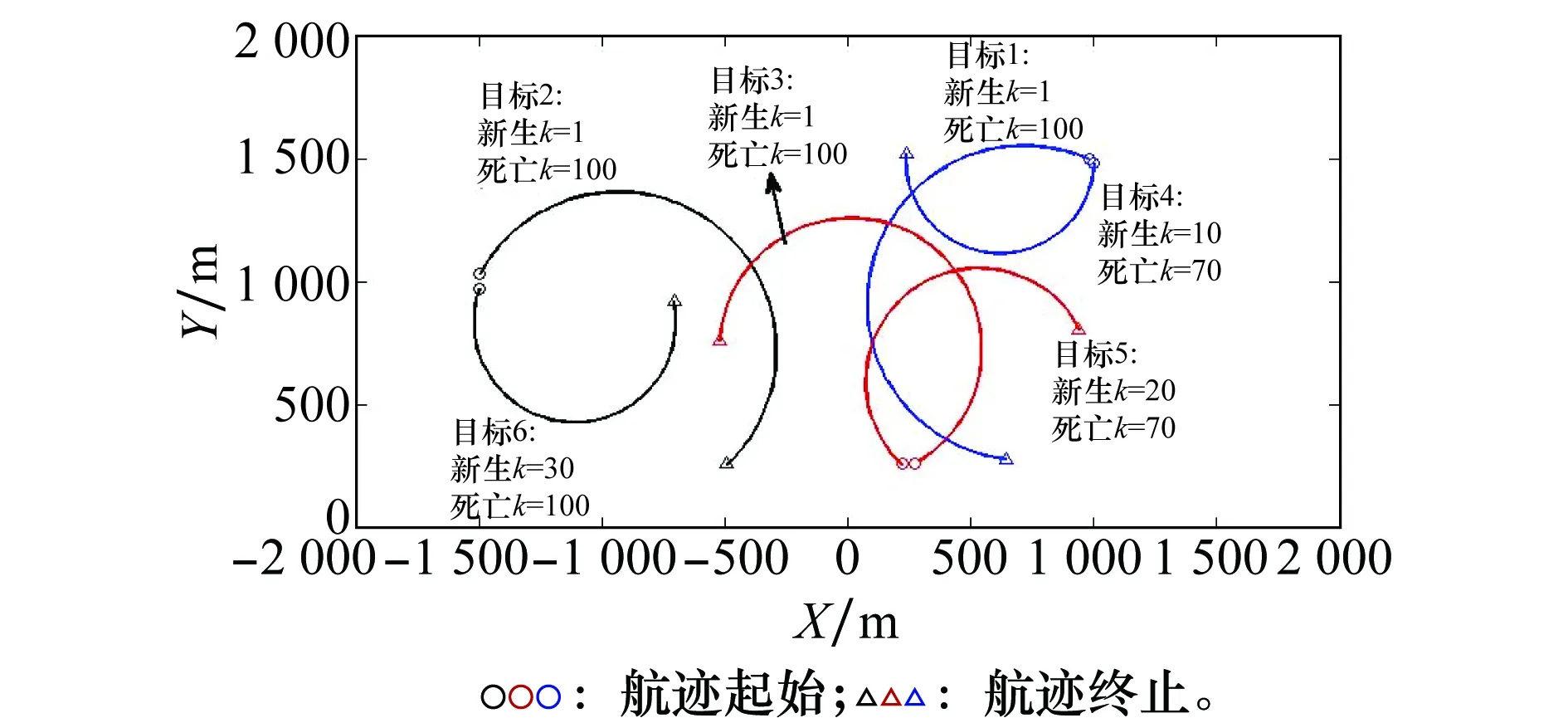
图1 目标真实轨迹Fig.1 True target trajectories

(25)

式中

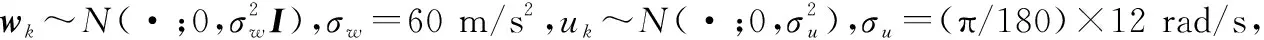
传感器测量模型为

(26)

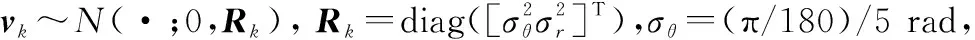
假设目标新生PHD为

(27)

式中

Pγ=diag([2 500 2 500 2 500 2 500 (6×π/180)2]T)

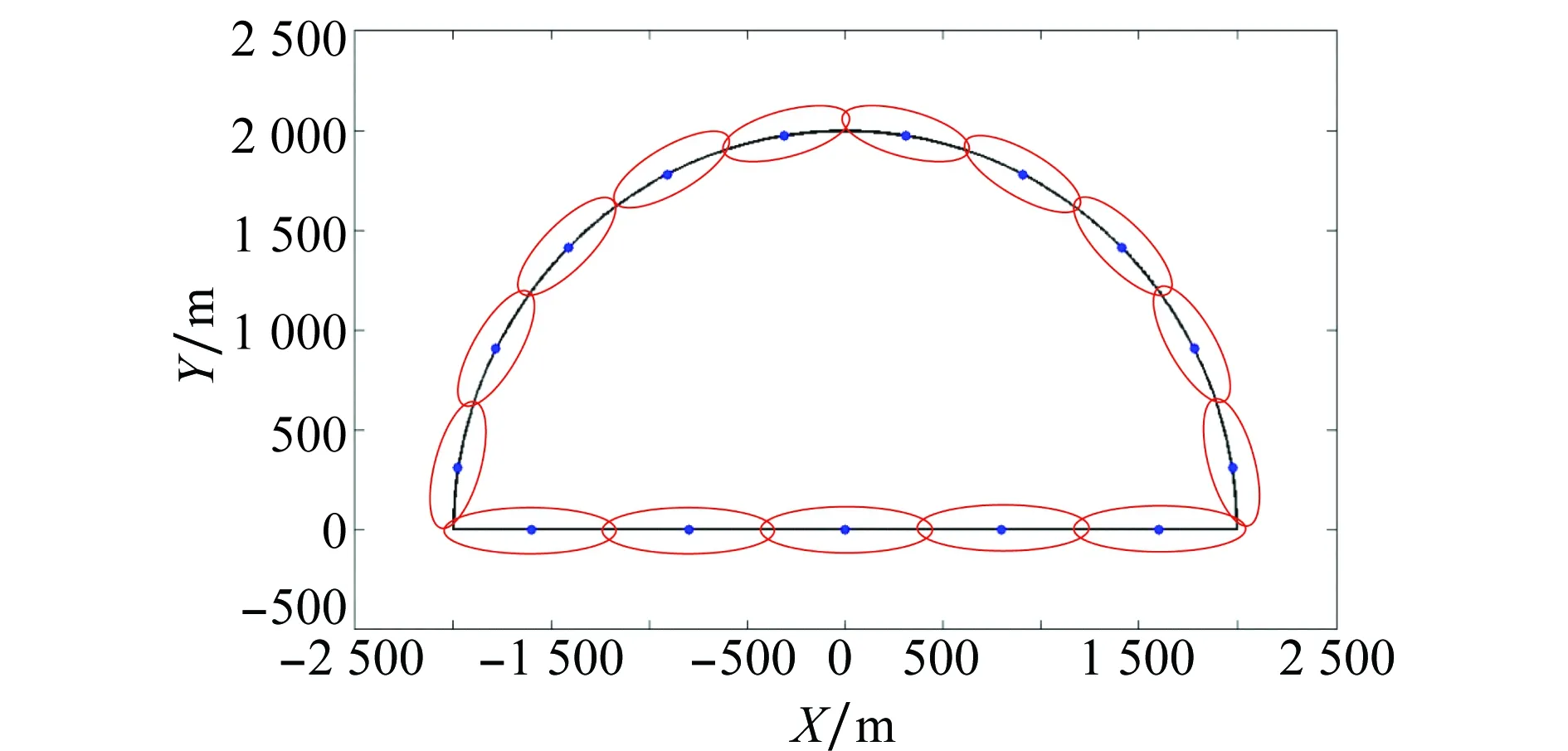
图2 新生PHD初始化Fig.2 Initialization of birth PHD

假设杂波服从泊松分布,每次测量杂波数目平均值为λ=20,且均匀分布在区域[-π/2,π/2]rad×[0,2 000]m内。目标存活概率和检测概率分别为PS=0.99,PD=0.98,粒子数M=300,递推更新次数N=20,蒙特卡罗仿真次数为MC=50。

另外,为消除高斯量的指数增长,设定权重剪枝门限T=10-5,合并门限U=4 m,高斯量最大数目Jmax=100,具体设置方法见文献[7]。

图3、图4分别给出传统GMP-PHDF[9]和本文SRRU-GMP-PHDF算法(利用CKF实现)在某一时刻的状态估计图,可以看出,相对于GMP-PHDF,SRRU-GMP-PHDF具有更优的状态估计性能。

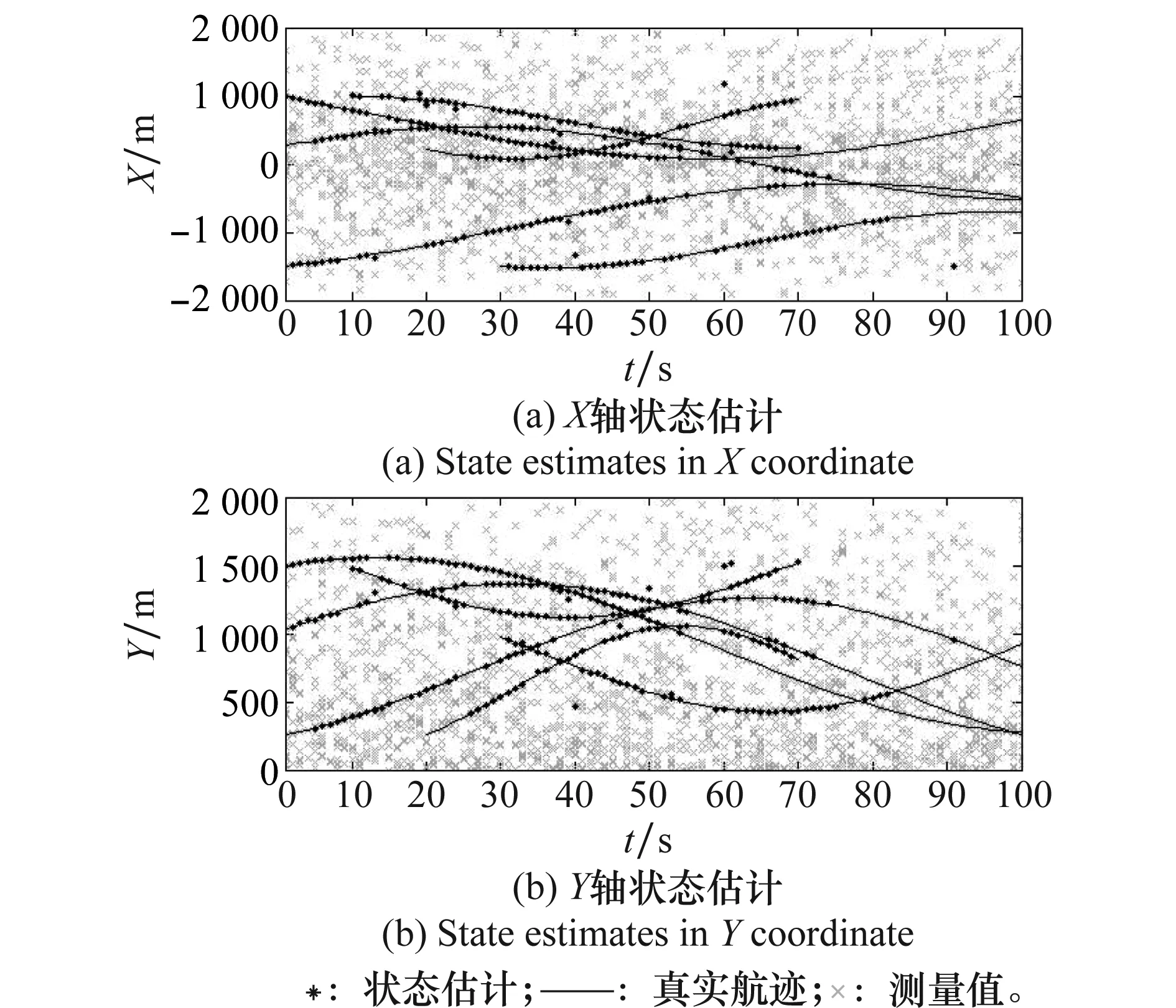
图3 GMP-PHDF状态估计Fig.3 State estimates of GMP-PHDF

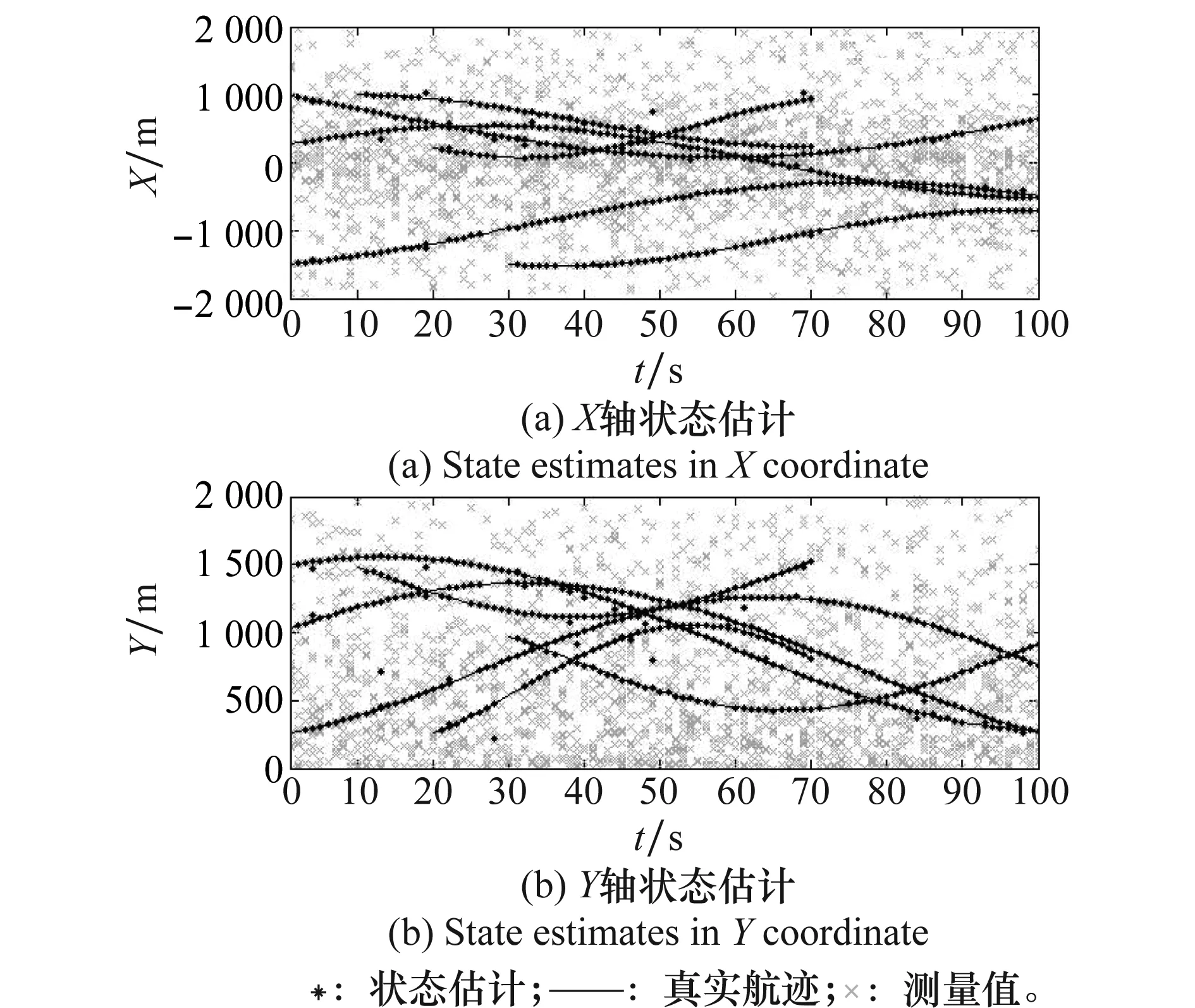
图4 SRRU-GMP-PHDF状态估计Fig.4 State estimates of SRRU-GMP-PHDF

此外,本文将SRRU-GMP-PHDF算法(利用CKF实现)与传统GMP-PHDF(以状态转移密度为重要性密度函数),CKF-GMP-PHDF(利用CKF产生重要性密度函数[13]),EKRU-GMP-PHDF(利用文献[15]递推更新方法产生重要性密度函数)进行性能对比。

图5给出各算法的最优分配模式(optimal subpattern assignment,OSPA)[21]性能对比图。不难发现,本文SRRU-GMP-PHDF算法和EKRU- GMP-PHDF算法的估计性能要优于其他两种算法,这表明递推更新思想的优越性及本文平方根递推更新方法的有效性。而EKRU-GMP-PHDF性能略差于SRRU-GMP-PHDF,可能的原因是EKF的线性化计算引入较大的滤波误差。传统GMP-PHDF的性能最差,且发散现象较严重,原因在于似然函数相对状态转移密度函数呈尖峰状态,导致其出现粒子退化问题,而CKF-GMP-PHDF性能优于GMP-PHDF,原因是其采用CKF结合最新量测产生重要性密度函数,有效缓解了粒子退化问题,但其在多目标临近情形时容易出现发散现象。

图5 OSPA性能对比Fig.5 Performance comparison of OSPA

图6给出各算法的势估计性能对比图,从中可以看出,在本文跟踪场景下,SRRU-GMP-PHDF算法的势估计值与真实值最为接近,说明本文算法势估计性能的有效性。EKRU-GMP-PHDF势估计性能略优于CKF-GMP-PHDF,而传统GMP-PHDF的势估计值与真实值相差最大,无法有效估计目标数目。

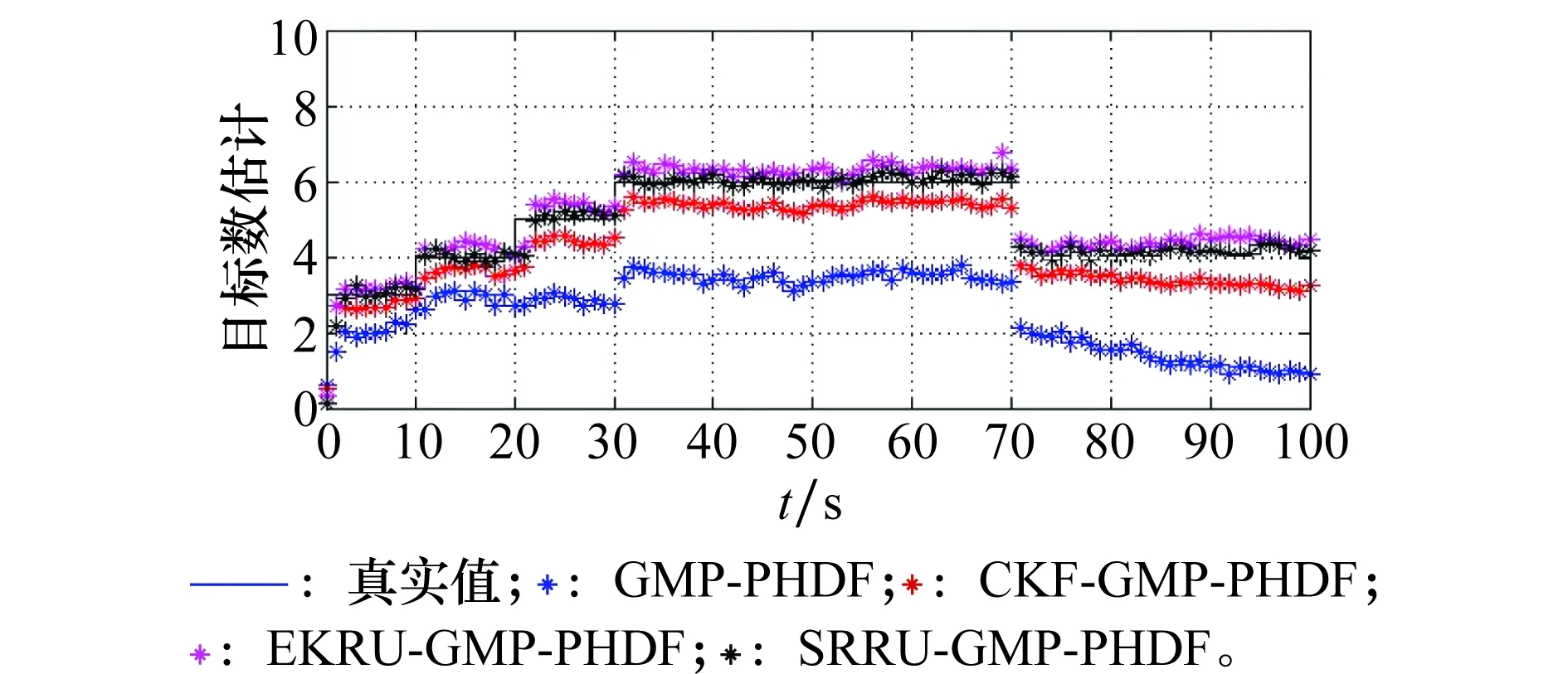
图6 势估计性能对比Fig.6 Performance comparison of cardinality estimates

表5给出各算法的单次运行时间对比,其中递推更新次数N=20。SRRU-GMP-PHDF 、EKRU-GMP-PHDF和CKF-GMP-PHDF的运行时间要明显高于GMP-PHDF两个数量级,原因是对于每一个重要性密度函数的选取,CKF-GMP-PHDF要利用CKF结合最新量测计算得到,而其他两种算法均进行N次的递推计算。SRRU-GMP-PHDF的运行时间最长,但其估计性能也最好。

表5 单次运行时间比较

图7和表6分别给出递推更新次数N=3,5,10,20时,SRRU-GMP-PHDF算法的OSPA及其均值对比。不难发现,随着N的增大,SRRU-GMP-PHDF算法性能逐渐提升。但是当N增加到一定程度时,SRRU-GMP-PHDF算法性能几乎不再提升。因此,实际应用时,应选取合适的递推更新次数,以权衡计算复杂度与估计精度。

SRRU-GMP-PHDFOSPA均值N=320.745N=515.871N=1015.437N=2015.428

5 结 论

传统GMP-PHDF采用先验状态转移概率密度作为重要性密度函数,会出现粒子退化问题。而RUGF可获得更为接近于真实分布的后验估计,但其协方差矩阵易非正定而导致递推中断。对此,本文首先分析SR-RUGF的实现思路,并利用SR-RUGF为GMP-PHDF构建重要性密度函数,进而提出SRRU-GMP-PHDF算法。仿真结果验证了本文算法的有效性。

参考文献：

[1] BA H X, CAO L, HE X Y, et al. Modified joint probabilistic data association with classification-aided for multi-target tracking[J]. Journal of Systems Engineering and Electronics, 2008, 19(3):434-439.

[2] REID D B. An algorithm for tracking multiple targets[J]. IEEE Trans.on Automatic Control, 1979, 24(6):843-854.

[3] STREIT R L, LUGINBUHL T E. Maximum likelihood method for probabilistic multi-hypothesis tracking[C]∥Proc.of the SPIE Signal and Data Processing of Small Targets, 1994, 2235: 5-7.

[4] MAHLER R. Multi-target Bayes filtering via first-order multi-target moments[J]. IEEE Trans.on Aerospace and Electronic systems, 2003, 39(4):1152-1178.

[5] VO B N, SINGH S, DOUCET A. Sequential Monte Carlo methods for multi-target filtering with random finite sets[J]. IEEE Trans.on Aerospace and Electronic Systems,2005,41(4):1224-1245.

[6] 王利伟,司伟建,曲志昱.增强型SMC-PHD多目标跟踪算法[J].系统工程与电子技术,2015,37(10):2205-2211.

WANG L W, SI W J, QU Z Y. Improved SMC-PHD algorithm for multiple targets tracking[J]. Systems Engineering and Electronics, 2015,37(10):2205-2211.

[7] VO B N, MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Trans.on Signal Processing, 2006, 54(11):4091-4104.

[8] KOTECHA J H, DJURIC P M. Gaussian particle filtering[J]. IEEE Trans.on Signal Processing, 2003,51(10):2592-2601.

[9] CLARK D, VO B T, VO B N. Gaussian particle implementations of probability hypothesis density filters[C]∥Proc.of the IEEE Aerospace Conference, 2007:1-11.

[10] MERWE R, DOUCET A, FREITAS N, et al. The unscented particle filter[C]∥Proc.of the 13th International Conference on Neural Information Processing Systems, 2000: 563-569.

[11] HOU S Y, HUNG H S, KAO T S. Extended Kalman particle filter angle tracking (EKPF-AT) algorithm for tracking multiple targets[C]∥Proc.of the International Conference on System Science and Engineering, 2010: 216-220.

[12] 康莉, 谢维信, 黄敬雄. 基于unscented粒子滤波的红外弱小目标跟踪[J]. 系统工程与电子技术, 2007, 29(1):1-4.

KANG L, XIE W X, HUANG J X. Tracking of infrared small target based on unscented particle filtering[J]. Systems Engineering and Electronics, 2007, 29(1): 1-4.

[13] LU C G, FENG X X, LEI Y, et al. A novel particle filter for nonlinear non-Gaussian estimation[C]∥Proc.of 3rd International Workshop on Intelligent Systems and Applications, 2011:1-5.

[14] HUBER M F, HANEBECK U D. Gaussian filtering for polynomial systems based on moment homotopy[C]∥Proc.of 16th IEEE International Conference on Information Fusion,2013:1080-1087.

[15] ZANETI R. Recursive update filtering for nonlinear estimation[J]. IEEE Trans.on Automatic Control, 2012, 57(6):1481-1490.

[16] 张勇刚,王刚,黄玉龙,等.递推更新高斯粒子滤波[J].控制理论与应用,2016,33(3): 353-360.

ZHANG Y G, WANG G, HUANG Y L, et al. Recursive update Gaussian particle filter[J]. Control Theory & Application, 2016, 33(3): 353-360.

[17] 何友,修建娟,关欣.雷达数据处理及应用[M].3版.北京:电子工业出版社, 2013.

HE Y,XIU J J, GUAN X. Radar data processing with applications[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2013.

[18] VAN DER M R, WAN E A. The square-root unscented Kalman filter for state and parameter-estimation[C]∥Proc.of the IEEE International Conference on Acoustics, Speech, and Signal Processing, 2001: 3461-3464.

[19] 刘华,吴文,王世元.基于平方根CKF的多传感器序贯式融合跟踪算法[J].系统工程与电子技术,2015,37(7):1494-1498.

LIU H, WU W, WANG S Y. Multi-sensor sequential fusion tracking algorithm based on square-root cubature Kalman filter[J]. Systems Engineering and Electronics, 2015, 37(7):1494-1498.

[20] 张召友, 郝燕玲, 吴旭. 3种确定性采样非线性滤波算法的复杂度分析[J].哈尔滨工业大学学报, 2013,45(12):111-115.

ZHANG Z Y, HAO Y L, WU X. Complexity analysis of three deterministic sampling nonlinear filtering algorithms[J]. Journal of Harbin Institute of Technology, 2013, 45(12): 111-115.

[21] VO B N, VO B T, SCHUHMACHER D. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Trans.on Signal Processing, 2008,56(8):3447-3457.