面向制造的圆弧齿线圆柱齿轮啮合接触冲击力研究*
马登秋,魏永峭,叶振环,刘小雍,侯 力
(1. 遵义师范学院 工学院,贵州 遵义 563006;2. 兰州理工大学 机电工程学院,兰州 730050;3. 四川大学 制造科学与工程学院,成都 610065)
0 引言
啮合接触冲击是指齿轮系统在工作过程中,由于主从动轮在齿轮副公法线方向上存在着相对速度,主动轮以一定的速度撞击从动轮的现象。该冲击碰撞行为严重影响齿轮传动的性能。因此,一些研究人员对齿轮传动过程中的啮合接触冲击展开了研究。例如,中南大学唐进元[1-2]利用商业有限元软件,对直齿轮啮合接触冲击进行研究,分析冲击速度和冲击位置对冲击应力、冲击合力和冲击时间的影响;对弧齿准双曲面齿轮啮合接触冲击影响研究,分析了齿面接触压强和最大瞬时接触力以及接触力和弯曲应力的波动情况,为改进齿轮的传动性能提供了一定参考。
圆弧齿线圆柱齿轮是一种新型齿轮传动,其齿向线是关于中截面对称的圆弧线,最早由日本学者为了解决直齿齿轮承载能力不足,将直齿齿向线替换为圆弧线而来,其传动、承载及润滑性能好、理论上无轴向力等优点[3]。目前,圆弧齿线圆弧齿轮的研究内容主要包括以下三个方面:
啮合原理[3-5]。主要涉及齿面方程、根切条件、传动条件、失配啮合、齿面修形等,为其实际应用奠定理论基础。
加工方法[6-9]。根据文献可以归结为以下几种:圆拉刀盘法,产品质量不稳定,成本高;三刀头切制法,效率低,精度不易保障;CNC数控加工法,未见其被推广使用;平行连杆式加工装置,效率低,系统刚度不高。
接触性能[3,10-12]。主要涉及到接触强度、弯曲强度、传动误差、啮合干涉、安装误差以及齿轮变位和中心距改变接触性能的影响、主要设计参数(齿宽、齿线半径和模数等)对传动性能的影响。
研究人员在这三个方面取得了丰富的研究成果,推动了该齿轮的应用。最为典型的应用是林光子将圆弧齿线圆柱齿轮替换齿轮泵中的直齿齿轮,解决了困油问题[13]。为了进一步推动圆弧齿线圆柱齿轮的实际应用,需要对圆弧齿线圆柱齿轮的冲击接触特性研究。例如,齿轮啮合接触冲击,啮入啮出冲击,节点冲击等。但是,并未见有关的研究报道出现,从制造的角度建模研究齿轮的啮合接触冲击更未见报道。
因此,本文拟探讨圆弧齿线圆柱齿轮的啮合接触冲击特性。文中根据圆弧齿线圆柱齿轮的齿面方程,建立面向制造的圆弧齿线圆柱齿轮CAD模型。运用ANSYS/LS DYNA软件分析不同冲击位置和冲击速度对齿轮径向、周向、切向啮合冲击力的影响规律,为该齿轮的设计进一步提供理论基础,特别是轴承的选用。
1 圆弧齿线圆柱齿轮啮合冲击模型
1.1 圆弧齿线圆柱齿轮加工方法
该齿轮自首次被提出后,主流加工方法有4种。
(1)大刀盘分度切制[6],如图1所示。大刀盘分为内、外刃切削区和两个分度区。在切削区,刀盘上安装了具有齿升量的刀片;在第一分度区安装工件。当刀盘旋转切削工件时,工件一边转动一边移动,刀盘旋转一周切出一个完整齿槽,然后反向转动和移动工件,对齿轮分度。这种加工方法可得到正常啮合的齿廓,但其刀盘直径较大,要求刀盘旋转速度低,对齿线半径的适用范围相对较小。由于该方法不能实现快速分度,齿轮加工效率较低。
(2)三刀头旋转切制[7],如图2所示。轮齿加工由三个工序形成:双刃刀具粗切齿槽;单刃刀具精切轮齿凸面;单刃刀具精切轮齿凹面。该方法与第一种方法类似,但可以得到较高精度的齿轮和保证齿轮法向齿槽宽相等,但该方法中刀具前刀面会旋转,所加工的齿轮在径向截面上分度圆处的压力角不相等。该方法需要分三次加工,需要多次对刀,操作十分不便。
(3)数控滚切加工[8],如图3所示。该方法加工效率高,但其刀具后刀面和已加工齿面容易产生干涉,加工半径较小的齿轮较困难,且轮齿中间厚两边窄,需要对其轮齿啮合特性进一步研究。
随着越来越多的农民工涌向城市,成为城市建设的重要组成部分,农村中小学“留守子女”的比例也越来越高。由于家长常年在外打工,缺乏对“留守子女”的正确引导和有效监护,往往使“留守子女”处于放任自流的状态,行为习惯较差,自控力普遍较弱。农村语文教师要探究激他们学习语文兴趣的措施,这是非常必要的。在近几年的初中语文教学中,我做了一些尝试。
(4)平动方法加工齿轮[9],如图4所示。这种加工方法借鉴了直齿圆柱齿轮的插齿加工方法,用基本圆弧齿条与齿坯作纯滚动,由啮合关系得到圆弧齿线圆柱齿轮。该种齿轮具有周向等齿厚、等齿槽宽的特点,接触线为一条圆弧线。但是该种加工方法得到的齿轮对轴向位移误差和角度误差以及中心距十分敏感,载荷分布的不均匀性较严重。另外,该种加工方法要求刀具平动,刀具中心平面法向不变。为了提高加工精度,这种加工机床仍处于研究阶段,目前只能加工软材料齿轮。
综上所述,现有加工方法存在一定的缺点,导致齿轮的应用没有得到推广。本文提出采用大刀盘双刃切削加工方法,可保证齿轮加工有较高的效率和精度,可实现磨削,改造或设计机床更加容易。图5所示为大刀盘铣削加工圆弧齿线圆柱齿轮示意图。该加工方法可以通过加工刀具的不同组合形式可以一次使齿轮轮齿和齿槽成形。在铣削成形齿槽时,先是通过铣削同时切出齿轮凹凸齿面,完成齿槽的切制,然后对齿坯进行分度,切制下一个齿槽,重复以上切削过程,最终完成齿轮的加工。
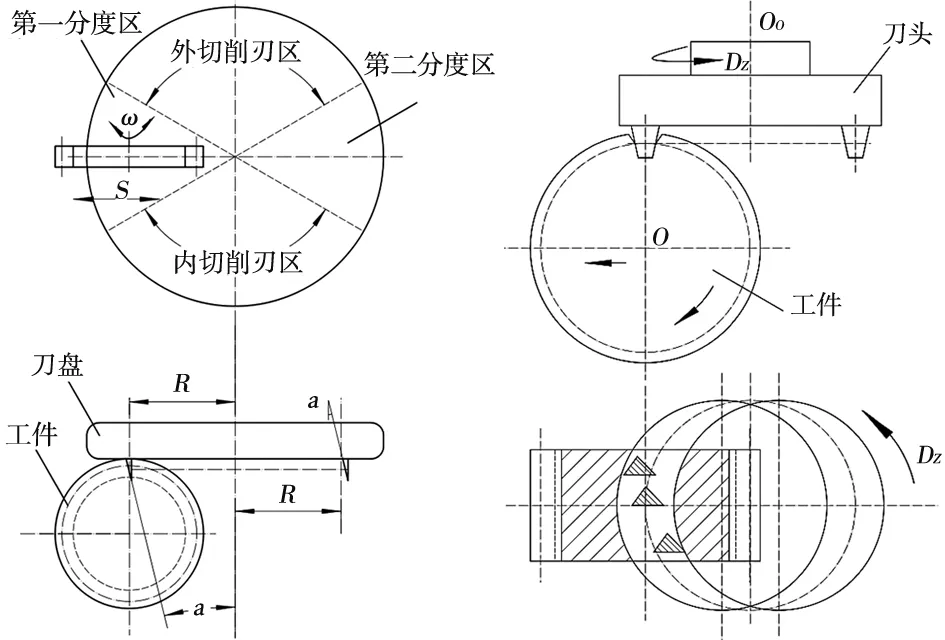
图1 大刀盘分度切齿 图2 三刀头切制圆弧齿线圆柱齿轮
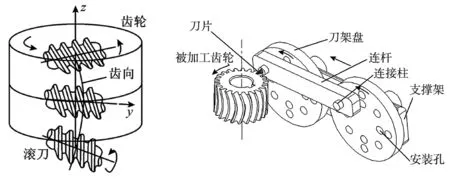
图3 数控滚切加工 图4 平行连加工圆弧齿线圆柱齿轮
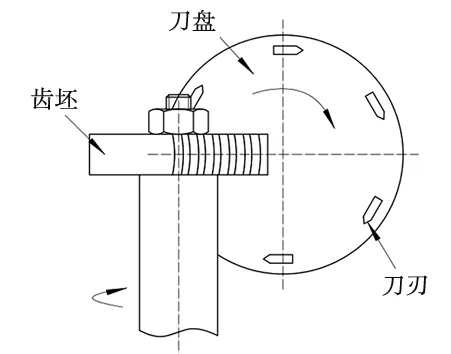
图5 大刀盘双刃切削加工
1.2 啮合接触冲击有限元建模
精确的几何模型是有限元分析的重要基础,为了得到准确的仿真结果,本文根据圆弧齿线圆柱齿轮的齿面方程,建立数学模型,获取齿面坐标,进而建立精确的三维模型。文献[14]给出了该齿轮齿面方程。
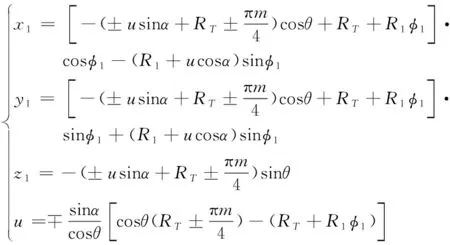
(1)
图6所示齿面数学模型和精确三维模型,在啮合接触冲击仿真分析中所用齿轮参数详见表1。
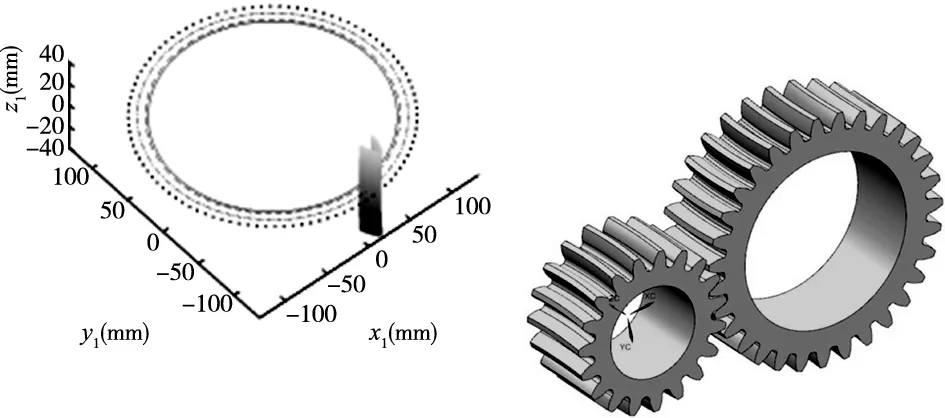
图6 圆弧齿线圆柱齿轮建模

齿轮参数主动轮从动轮齿数1931模数88齿宽80mm80mm压力角20°20°齿线半径500mm500mm中心距 200mm
根据上述建立的精确三维模型,建立不同啮合位置发生啮合接触冲击仿真的有限元分析模型,但为了避免相邻轮齿间的影响,仅保留从动轮上的一个轮齿,有限元建模主要步骤如下。
(1)材料参数与约束设置。主动轮各自由度中保留Z轴旋转,从动轮约束全部自由度。材料参数:密度为7850kg/m3,弹性模量为210GPa,泊松比为0.28。
(2)网格设置与划分。模型网格单元类型选择solid164单元和shell163单元,齿轮整体用solid164单元划分网格,齿轮内圈表面采用shell163单元划分网格。用扫略的方式进行划分,保证网格质量。
Edcgen, asts, 2, 1, 0.2, 0.1, 0, 0, 0,…,0, 1e21,0,0
Set, VVET1 (6, 1, 1), 10
Edipart, 3, add, center, 5.52094, 0, II, VVET1, 11 Edipart, 4, add, center2, 0.43469, 0, II2, VVET2, 12
Edcgen, asts, 1, 2, 0.2, 0.1, 0, 0, 0,…,0, 1e21, 0, 0,
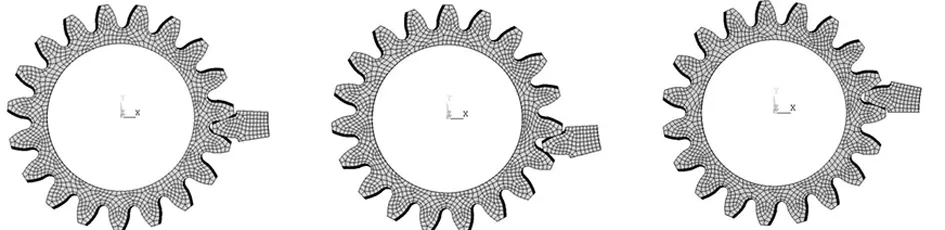
(a)分度圆附近 (b)齿顶附近 (c)齿根附近图7 啮合接触冲击有限元分析模型
2 啮合接触冲击力分析
齿轮传动系统中,齿轮各个方向上所啮合力对齿轮传动系统整体的性能有着重要影响,例如轴承选择、锁紧装置、润滑等等。通过仿真得到各冲击位置不同冲击速度下各个方向的冲击力,即图8~图16,其中图8~图10为径向冲击力,图11~图13为切向冲击力,图14~图16为轴向冲击力。根据相关图表可以得到以下结论:
(1)径向、切向和轴向三个方向冲击力相比,径向、切向冲击力较大,且呈现抛物线变化规律;轴向较小,基本可以忽略不计,且变化无规律,圆弧齿线圆柱齿轮结构轴向关于中截面对称,理论上该齿轮轴向不存在啮合力,这一特点得到验证。
(2)无论是齿顶附近冲击、齿根附近冲击还是分度圆附近冲击,随着冲击速度增大,径向、切向方向冲击力越大。轴线方向冲击力随着冲击速度的变化无明显变化。
(3)关于冲击位置对冲击力的影响,根据曲线图,相同冲击速度时,径向冲击力齿顶附近冲击最大,分度圆附近冲击次之,齿根附近冲击最小;切向冲击力分度圆附近冲击最大,齿根附近冲击次之,齿顶附近冲击最小;轴向变化无规律。
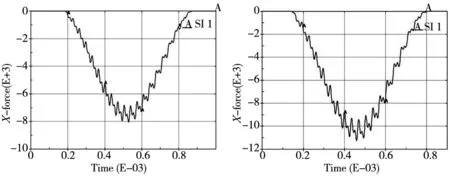
(a)冲击速度10rad/s (b)冲击速度13rad/s
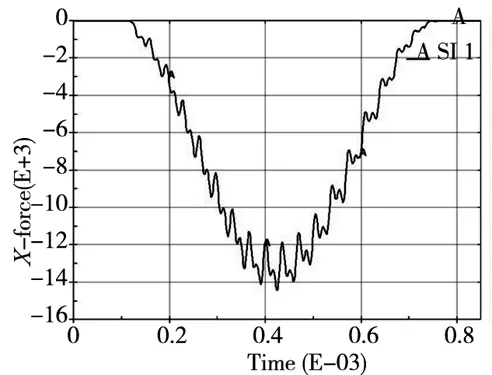
(c)冲击速度16rad/s图8 分度圆位置附近冲击径向冲击力
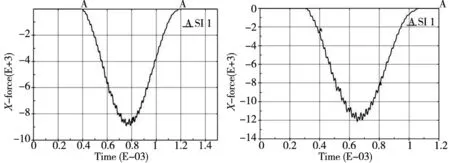
(a)冲击速度10rad/s (b)冲击速度13rad/s
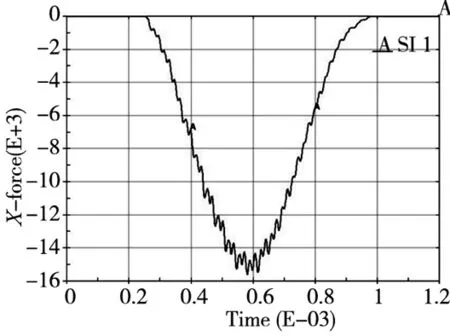
(c)冲击速度16rad/s图9 齿顶位置附近冲击径向冲击力
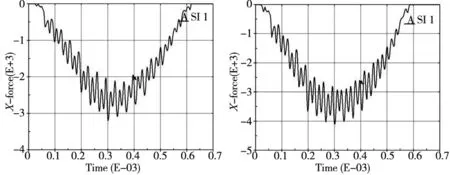
(a)冲击速度10rad/s (b)冲击速度13rad/s

(c)冲击速度16rad/s图10 齿根位置附近冲击径向冲击力
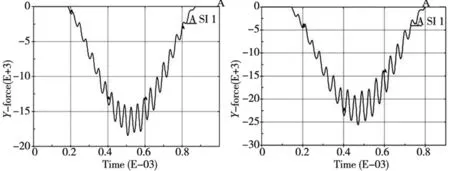
(a)冲击速度10rad/s (b)冲击速度13rad/s
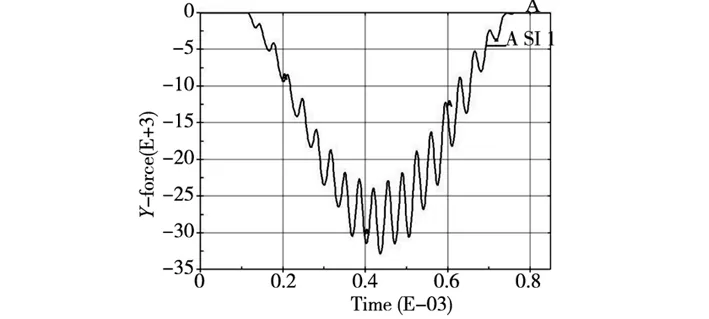
(c)冲击速度16rad/s图11 分度圆位置附近冲击切向冲击力

(a)冲击速度10rad/s (b)冲击速度13rad/s

(c)冲击速度16rad/s图12 齿顶位置附近冲击切向冲击力
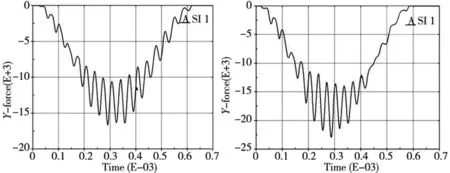
(a)冲击速度10rad/s (b)冲击速度13rad/s

(c)冲击速度16rad/s图13 齿根位置附近冲击切向冲击力

(a)冲击速度10rad/s (b)冲击速度13rad/s

(c)冲击速度16rad/s图14 分度圆位置附近冲击周向冲击力

(a)冲击速度10rad/s (b)冲击速度13rad/s
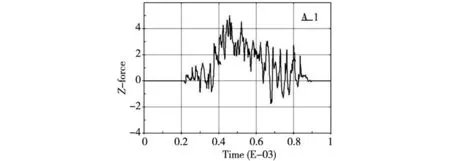
(c)冲击速度16rad/s图15 齿顶位置附近冲击周向冲击力
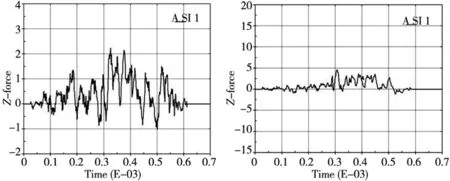
(a)冲击速度10rad/s (b)冲击速度13rad/s

(c)冲击速度16rad/s图16 齿根位置附近冲击周向冲击力
3 结论
本文分析了圆弧齿线圆柱齿轮的加工制造方法,给出了面向制造的圆弧齿线圆柱齿轮齿面方程,建立面向制造的圆弧齿线圆柱齿轮精确数字模型。运用软件分析不同冲击位置和冲击速度对齿轮径向、周向、切向冲击力的影响规律,结果表明:
(1)径向、切向和轴向三个方向冲击力相比,径向、切向方向上冲击力较大,且呈现抛物线变化规律;在轴线方向较小,且呈现无规律变化。
(2)无论是齿顶附近冲击、齿根附近冲击还是分度圆附近冲击,随着冲击速度增大,径向、切向冲击力增大,轴线方向冲击力随着冲击速度的变化无明显变化。
(3)相同冲击速度时,径向冲击力齿顶附近冲击最大,分度圆附近冲击次之,齿根附近冲击最小;切向冲击力分度圆附近冲击最大,齿根附近冲击次之,齿顶附近冲击最小;轴向变化无规律。
[参考文献]
[1] 唐进元, 周炜, 陈思雨. 齿轮传动啮合接触冲击分析[J]. 机械工程学报, 2011, 47(7):22-30.
[2] 姚启萍, 唐进元. 弧齿准双曲面齿轮啮合接触冲击有限元仿真分析[J]. 铁道科学与工程学报, 2011,8(4): 111-115.
[3] 狄玉涛. 弧齿线圆柱齿轮传动理论的研究[D].哈尔滨:哈尔滨工业大学,2006.
[4] 狄玉涛,陈明.弧齿线圆柱齿轮齿面形成原理及啮合性能分析[J]. 机械工程师,2006 (9):50-52.
[5] 马振群,王小椿,沈兵.对称弧形齿线圆柱齿轮的真实齿面接触分析研究[J].西安交通大学学报,2005,39(7):722-726.
[6] 邹旻. 圆弧齿线圆柱齿轮的参数计算及选择[J]. 机械设计与研究, 2000(2): 36-38.
[7] 寇世瑶, 刘明保, 武良臣. 弧齿圆柱齿轮加工的新方法[J]. 现代制造工程, 2002(9): 16-17.
[8] 戴玉堂, 有贺幸则, 姜德生. 圆弧齿线圆柱齿轮的数控滚切机理与试验研究[J]. 机械工程学报, 2006, 17(7): 706-709.
[9] 宋爱平, 吴伟伟, 高尚, 等. 弧齿圆柱齿轮理想几何参数及其加工方法[J]. 上海交通大学学报, 2010,44(12):1735-1740.
[10] 吴伟伟,宋爱平,王召垒. 渐开线弧齿圆柱齿轮的齿根应力分析[J]. 机械设计与制造,2009(11):227-229.
[11] 王召垒, 宋爱平,陈婷.渐开线弧齿圆柱齿轮副齿面接触应力分析[J]. 机械设计与制造, 2008 (12) : 188-191.
[12] 王少江,侯力,董璐. 面向制造的弧齿圆柱齿轮建模及强度分析[J]. 四川大学学报:工程科学版, 2012,44(2):171-175.
[13] 林子光. 能连续泵油的曲线齿轮油泵[P]. 中国专利: ZL 94223886.9, 1995-12-03.
[14] 赵斐, 侯力, 段阳,等. 旋转刀盘圆弧齿轮成形理论分析及数字化建模研究[J]. 四川大学学报:工程科学版, 2016, 48(6):119-125.

