直列式两级四缸气动发动机性能仿真*
周 鑫,潘孝斌
(1.中船重工第七一五研究所,杭州 310023; 2.南京理工大学 机械工程学院,南京 210094)
0 引言
随着生态环境破坏和石油资源枯竭,新能源开发和高效率利用技术迫在眉睫。压缩空气能量密度高,对环境无污染,是适合汽车的绿色动力能源。气动汽车作为新一代的能源汽车,采用气动发动机为动力装置,以压缩气体的原理来驱动汽车,所以出于车载的特殊性,能否合理的设计好这款新型发动机直接影响到汽车的用户体验[1]。
车载的动力源是通过压缩的空气,就目前高压储存容器的储存容积有限,经过减压器减压至工作压力释放到气动发动机膨胀做功,大多高压气源减压方式为节流减压,为快速获得动力,以牺牲减压过程的大量膨胀功为代价而得以实现的,所以我们要合理的利用好减压过程中的膨胀功。故设计一款高气动效率而不失气动功率的气动发动机迫在眉睫。
单气缸发动机具有振动大、气体效率低、输出扭矩不稳定,造成不必要的能源浪费[2],本文在单缸气动发动机的设计理念上,尝试实现直列、多缸、多级的气动发动机传动研究,缩短气动传动系统的尺寸参数设计周期,并将气动效率大大的提高了。针对直列式两级四缸气动发动机的工作特性,本文通过结合动力学和热力学原理综合计算分析,对直列式两级四缸气动发动机结构性能进行分析研究,考量各参数变量对气动传动系统的影响,并为多级多缸的气动发动机设计与研究提供理论基础[3-5]。
1 单缸发动机膨胀做功原理和特点
1.1 单缸发动机结构和原理
单缸发动机的结构设计示意图如图1所示,图中的变量参数代表的物理量见表1,起始的气源参数通过下标0表示,1、2分别表示气缸无杆腔室和有杆腔室变量参数。把单缸发动机结构简化成,其结构原理实质是曲柄滑块结构,这个工作过程:冲程阶段,高压气体从无杆腔室进气膨胀做功,带动曲柄旋转180°;回程阶段,高压气体从有杆腔室进气膨胀做功,曲柄转动回归初始位置,进而周期性往复运动。
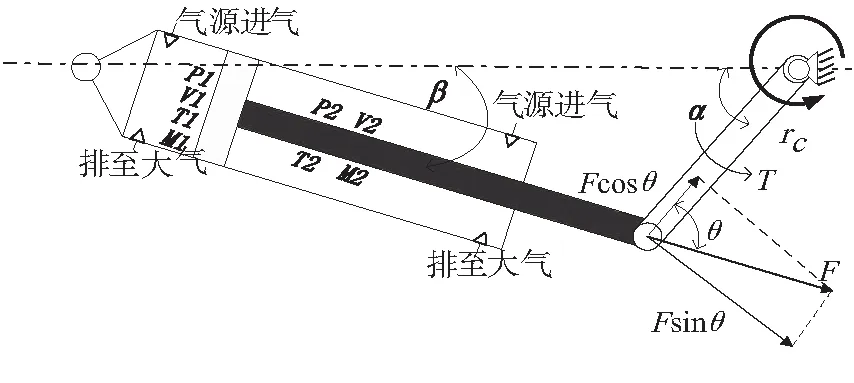
图1 单缸发动机结构
1.2 直列式两级四缸气动发动机的结构和原理
在单缸发动机基础上,设计的直列式两级四缸气动发动机如图2所示,由于四缸是通过一根曲轴连接四个活塞连杆,一个缸做完功后等曲轴转180°再让另一缸做功,这样同时两缸出现在上止点,两缸出现在下止点,气源“点火”才能平均,并且同上同下解决了结构垂直方向的振动;考虑到端面到端面的振动,设计出两个气缸产生一个相反的端到端扭力来抵消1、2缸制造出的端到端的扭力,所以最终1、4缸同水平高度,2、3缸同水平高度,并以相位相差180°安装。结构图参数如表1所示。

表1 示意图参数代表的物理量

图2 直列式两级四缸气动发动机结构
在冲程阶段,高压储气罐通过减压阀,将气源压力降至工作压力,经过气管元件将气源排入第一、第四气缸无杆腔室,待腔内气体到达到自由膨胀的压力,有杆腔室将残余压力排入第二、三气缸的无杆腔室,第二级气缸进行第二次膨胀做功,在整个做功的冲程中曲柄旋转转180°;在回程阶段,气源经过气管元件将气源排入第一、第四气缸有杆腔室,待腔内气体到达到自由膨胀的压力,无杆腔室将残余压力排入第二、三气缸的有杆腔室,第二级气缸进行第二次膨胀做功,最终曲柄回归初始位置,完成一个循环周期运转,如此周期性往复工作。
2 直列式两级四缸发动机数学模型研究
由于气压传动系统整体工况相对复杂,出于简化计算和便于分析,列出如表2假定。

表2 假设条件
2.1 单缸发动机数学模型
由于单缸发动机的结构是变质量系统模型可知,故根据热力学第一定律有[6]:
dQ1+i0dM0=dU1+dW1+i1dM
(1)
气体进入腔室1至排出时间极短,室内的气体来不及与外界进行热交换,改过程可视为绝热放气过程:
dQ=0,dM1=0
(2)
经过整理简化有:
kRT0dM0=dp1V1+kp1dV1
(3)
代入配气行程比,等式两边分别对时间求导,可得工作腔压力变化方程式:
(4)
同理腔室2的气动方程为:

(5)
流量公式计算表示为:

(6)
按图1结构进行受力分析,并建立动力学平衡方程:

(7)
式(4)~式(8)构成单缸发动机的数学模型方程,模型方程中参数代表的物理量如表3所示。

表3 参数方程参数代表的物理量
2.2 直列式两级四缸气动发动机数学模型
直列式两级四缸气动发动机系统结构基本和单级相同,两个气缸通过串联方式相连接,根据单缸发动机的建模理论原理和图2所示的直列式两级四缸气动发动机结构,可以得出直列式两级四缸气动发动机的热力学方程和动力学方程,分别为:
(8)
对图2中结构进行受力分析,并建立动力学平衡方程:

(9)
联立式(7)~式(9)即为直列式两级四缸气动发动机的数学模型,模型方程中参数代表的物理量如表4所示,下标X表示第一、二、三、四气缸。

表4 参数方程参数代表的物理量
3 仿真结果与分析
3.1 直列式两级四缸气动发动机性能分析
直列式两级四缸气动发动机的数学模型都是一组常微分方程,并运用四五阶龙格库塔法,进行编程求解。仿真参数如表5所示。
图3为直列式两级四缸气动发动机工作稳定运转时,分别为一个周期循环内一级和二级气缸有杆腔和无杆腔的压力变化图,从图3中可以看出:在相位差为180°的各气缸两个腔室的压力变化大小的趋势基本上是一致的。第一级的一、四两缸在膨胀做功终了时,还剩余0.55MPa。由于0.55MPa的压力高于大气,为了提高气动效率,系统将剩余的压力气源通过气管元件注入二级气缸无杆腔,并进行膨胀做功,做功终了时排入大气的压力为0.102MPa左右,几乎达到与大气压等同的压力。由此可见,在0.8MPa工作压力的情况下,直列式两级四缸气动发动机能够通过设计成多级多缸的形式,来达到提高有压气体的做功效率,不但节约了气源压力能,避免浪费,最终还提高了气动效率。

表5 仿真初选参数

图3 气缸内部压力变化曲线
图4显示了一个循环周期内曲轴稳定运转时,输出的瞬时扭矩、平均扭矩及各缸的扭矩变化图,从图上可以直观的看到,在一个循环工作周期之内,曲轴能够向外提供的输出瞬时最大扭矩为42.78 N·m,并且平均向外输出扭矩为非常稳定的26.1 N·m。图5为车辆从气动发动机启动的瞬间到输出扭矩稳定整个工作过程的速度变化图,为了在仿真过程中快速达到稳定循环速度,起初采用较小的传动比。通过扭矩与速度公式换算成车辆的行驶的速度为37km/h,满足对于一般汽车行驶设计要求。

图4 曲轴瞬时扭矩输出变化

图5 车辆行驶速度曲线
3.2 气动效率和气动功率的影响因素
对于评估气动系统的性能指标有很多,但是最重要的两项性能指标为:气动效率和气动功率。本文主要根据直列式两级四缸气动发动机建立数学模型,选取出4个核心的参数,分别讨论与研究在稳定工作过程中,系统配气过程的配气行程比例(整个做功充气行程和自由膨胀行程的比值)、气缸缸体直径、程径比(气缸行程与缸径的比例)、气缸整个工作行程传动比(从曲轴输出到最终传递到实输出扭矩之比)对气动系统的效率的影响。气动系统效率、气动功率表达式[7]表示为:

(10)
其中,w为汽车车轮的角速度。
为了实现气动系统高扭矩,低转速设计理念,需配合不同传动比的增速器进行速度调节。介于气缸尺寸参数是通过查表选型得到的,而且是确定的,故影响系统气动效率的主要因素为传动比和配气行程比,接下来本文需要针对系统效率的传动比和配气行程比例两项重要影响参数进行进一步的讨论。
从理论上分析,传动比与气动效率是成线性关系的,随着系统传动比递增,气动效率也伴随着提高,但是由于系统空间的局限性,传动比只能在合理的范围内相应增大;在发动机稳定运行的系统中,配气行程比例假设越小,那么产生的效果是气动效率提高。
传动比和配气行程比例两参数是具有相关性的,单独考量某一参数,都只会片面的反映对系统气动效率的影响。本文综合考虑,耦合了传动比和配气行程比例系统气动效率的影响。

图6 传动比影响气动效率曲线
图6为传动比和不同配气行程比例耦合对气动效率影响曲线。图6直观的验证了理论的分析,传动比与气动效率是成正相关的线性关系,因为负载所需的扭矩逐渐增加,使得执行气缸正常运转速度减慢,运作时间的加长,使工作有压气体在气缸内充分、高效膨胀做功。同样的系统气动效率,配气行程比越大,增器传动比值也应当增大,故直列式两级四缸气动发动机的低转速、高扭矩的特性大大提高了系统的气动效率。
图7为传动比影响系统气动功率的特性曲线,可以看出配气行程比与系统所能输出的最大功率成正相关的关系,配气行程比增大,系统输出功率提高,伴随着运行的动力性能就越好。通过分析图6和图7的特性曲线,可以表明:要达到相同的气动功率,不同的传动比需匹配不同的配气行程比值,即传动比与配气行程比值相互耦合影响着系统的气动效率,同理不能片面的认为功率越大效率越高,当且仅当负载率[8](即系统输出功率与系统能输出最大功率比)变小时,气动效率才会提高。

图7 传动比影响功率曲线
对于直列式两级四缸气动发动机中执行气缸的选型也是十分重要的,搭配不同系列类型的行程和缸径左右着整个系统的动力性能。在原来的参数基础上,取程径比0.6~1.3的值进行仿真。
第一级气缸(一、四缸):从图8上曲线的走势可以看出:气缸的程径比与系统的气动效率是成正相关的,气缸的程径比值增加,整个气缸的行程越长,压缩气体在缸内自由膨胀就越充分,膨胀终了的残余压力就越小,在开始运动的过程,气缸的两个腔室的背压也就相应减小,输出的总扭矩变大,在整个冲程阶段的输出功率也就越大。气动发动机的功率与程径比成负相关的,尽管程径比的增大带来了气动效率的提高,但在程径比增大的过程,整个运转机构也开始慢起来,伴随着一个循环运转周期也加长了,在相同的时间内,程径比越大的输出做功就变少了,输出的功率也降低了。

图8 第一级缸程径比影响曲线
第二级气缸(二、三缸):从图9上曲线的走势可以看出:二级气缸的程径比对系统的气动效率基本没有影响,因为整个运转机构的效率是有第一级气缸的气源进气流量和发动机的自由膨胀充分决定的,在气体容积不变的情况下,两级气缸输出的共都是相等的,所以可以判定两级四缸发动机两级气动效率主要是由一级气缸程径比决定的,与第二级缸无太大关系。二级气缸的程径比与系统的输出功率成正相关的关系,总体趋势是随着程径比增大,输出功率增加,最后趋于稳定的状态;当气缸程径比值小时,曲轴的转速比较慢,尽管膨胀做功充分,但是单位时间内输出的膨胀功小;当气缸程径比值增大时,行程不变,缸径变小,气缸的运动质量减小,在冲程的加速阶段,运转机构的加速度增大,机构稳定后的转速也增大,单位时间内的输出功、输出膨胀功也增加,且随着程径比的增加,最后功率变化趋于稳定。

图9 第二缸程径比影响曲线
3.3 与单级气缸发动机仿真比较
本文的直列式两级四缸气动发动机是在单级气动发动机的基础上建立的数学模型,所以为了更好的展示直列式两级四缸气动发动机的优点,接下来将对单级发动机进行仿真对比,设定的参照准则:最终稳定的运行速度可以达到设计时速:36 km/h。表6为单级气动发动机的仿真参数。

表6 仿真参数
从图10上可以看出:单级气动发动机膨胀做功后,将还有0.53MPa的残余压力释放入大气,造成了不必要的浪费;由于单腔膨胀做功后残余的压力较大,在切换腔室即回程的时候,无杆腔室背压大,大大地增加了负向扭矩,最终导致总的输出扭矩减小。直列式两级四缸气动发动机实现多级膨胀,将剩余的残余压力合理有效利用起来。

图10 两级与单级气动发动机压力对比曲线
4 结束语
本文通过动力学和热力学原理分析建立的对直列式两级四缸气动发动机数学模型可以很好的揭示这一类型的发动机工作特性,在此基础上的仿真研究可以得出以下几个结论:
(1)应用于小型汽车上的气动发动机,直列式两级四缸气动发动机更能够适应标准有压气源的运行要求,实现了低转速,高扭矩的工作特性,保证了对系统的精确控制,适应性更强,使得运行机构配合装配起来更便捷。
(2)在通入标准的工作压力,能带动负载运转的情况下,可以匹配不同的传动比值和配气行程比值,但仿真发现最终的气动效率都是51.2%,所以可以根据整个运转机构的体积搭配不同的比值。
(3)在设计直列式两级四缸气动发动机时,能实现设计时速的情况下,第一级气缸尽肯能的选择程径比值大的系列,并且根据负载的功率去选择第二级气缸的程径比,第二缸的程径比对整个系统的气动效率无明显影响,合理控制负载率降低有利于提高气动效率。
(4)在同样的工作压力下,列式四缸气动发动机相比于单缸发动机有系统气动效率高(51.2%),输出扭矩平稳,运动稳定性高,传导换热充分等优点。
[参考文献]
[1] 丁廷哲,潘孝斌. 两级膨胀器性能仿真[J]. 液压与气动,2016(10):52-56.
[2] 朱烨. 两级气动发动机性能影响因素分析与优化[D].合肥:安徽农业大学,2015.
[3] 王文彪,谈乐斌,潘孝斌. 基于AMESim的容积式高压气体减压系统的仿真研究[J].机床与液压,2014(11):157-159.
[4] 方清华. 压缩空气/燃油混合动力发动机工作特性的数值模拟[J]. 中国机械工程,2012,23(5):620-625.
[5] 许启跃. 气动发动机多参数多目标寻优方法[J]. 北京航空航天大学学报,2013,39(6):803-807.
[6] 潘孝斌. 二级膨胀往复式气动发动机设计与仿真[J]. 南京理工大学学报,2014,38(4):439-444.
[7] 蔡茂林. 气动系统的能量消耗评价体系及能量损失分析[J]. 机械工程学报,2007,43(9):69-74.
[8] Di Liming .Design and operating characteristics of a variable load rate engine[J]. International Journal of Simulation: Systems, Science and Technology,2016,6(6) :2.1-2.8.

