基于D-H法的摄影机器人运动学分析
赵宇豪,韩 军,欧 屹
(南京理工大学 机械工程学院,南京 210094)
0 引言
虚拟演播室作为近几年兴起的电视节目制作手段,有着传统演播室不可比拟的优势。虚拟演播室能够将虚拟场景或者物件和真实的人或物合成到同一台电视画面上,为节目制作提供了更大的空间[1]。虚拟演播室中不可或缺的就是带位置跟踪功能的摄影机器人[2]。摄影机器人的控制过程与一般工业机器人不同[3],在媒体行业的使用中,操作人员不会使用坐标参数,而是从拍摄画面获得需要的信息。因此需要结合此种使用习惯完成运动学分析,提出一种镜头随动拍摄算法。
工业机器人运动学分析中,Waldron和Paul、Craig修正的D-H算法已经非常普遍[4],也有很多用D-H算法分析的工业机器人;PTZ云台姿态测量和配套的虚拟演播室合成在国内也有一些成果[5]。但摄影机器人随动拍摄的运动学分析在国内仍属空白。本文从D-H连杆算法出发,通过分析本摄影机器人结构,提出摄影机器人工作末端的新分析方法,通过MATLAB正反解验证后,编写机器人运动控制程序,通过实验在拍摄时验证该算法。该算法可使云台自动跟踪拍摄,解决了摄影机器人控制的重要问题。
1 摄影机器人结构设计与工作要求
1.1 结构设计
图1所示为摄影机器人三维示意图,由云台部分完成摄像机偏转和俯仰;升降部分完成摄像机抬升和下降;行走部分通过聚氨酯轮在轨道上行走完成机器人整体移动;摄像机镜头上装有镜头编码器,可以测量变焦聚焦齿轮转过的角度。

图1 摄影机器人结构示意图
1.2 工作要求
摄影机器人通过4个自由度控制摄像机,使摄像机可以达到轨道覆盖的指定位置和指定角度。一般情况下,操作人员通过控制各轴直接控制摄像机位置,观测当前拍摄画面修正控制效果。
在自动控制时,摄影机器人操作人员点击视频上一点,摄像机云台就会将被点击的目标持续置于画面中心。这种控制方式需要将在屏幕中采集的二维坐标转换为对应三维空间的坐标点,且根据该点坐标和已知状态对PTZ云台参数进行反解。
2 摄影机器人运动学建模
2.1 虚拟连杆
传统的D-H法通过连杆参数描述机器人末端执行器相对于参考系的变换关系,这种方法在工业机器人上有广泛应用。传统机器人工作末端操纵工件等物体,运动结果直接反应在物体的空间位移上;摄影机器人工作末端操作摄像机,运动虽然直接反应在摄像机空间位移上,不能从拍摄画面获得。仅对物理连杆的建模无法将摄像机空间位置和拍摄画面联系起来。此时,就需要分析镜头焦距特性,将焦距特性转化为一个虚拟连杆,用以表征摄像机拍摄的实际位置。该虚拟连杆可将工作末端从摄像机本身扩展至整个可拍摄空间。
从二维画面中计算三维坐标最重要的是获得摄像机和拍摄物体的距离,而变焦镜头当前焦距则可以反映该距离。镜头厂商在生产某型号镜头后,一般会提供变焦齿轮全行程与焦距实际值的函数关系;在没有得到该函数关系时,也可以通过视觉识别的方法测量焦距[6-8]。当得到该函数以后,通过自研镜头伺服器,测出变焦齿轮当前转过的角度,转化为焦距。将该焦距变化作为虚拟的棱柱联轴节,生成一个虚拟连杆,作为摄影机器人的第四连杆。镜头伺服器实物如图2所示。

图2 镜头伺服器
2.2 改进的D-H连杆模型

图3 摄影机器人改进D-H坐标系
通过根据焦距扩展的D-H连杆模型,建立摄影机器人坐标系[4,9],如图3所示,其中df为第4连杆伸缩距离。表1为D-H法的各个参数,其中a3为摄影机安装在云台上的误差,一般大小在±20mm以内,其值很小可以忽略;dw的距离为轨道长度。表2为各参数取值范围,行走使用的是6m的直线轨道;升降和俯仰范围由机械结构限制;聚焦距离要按照具体镜头的最小值和最大值确定。

表1 摄影机器人D-H参数

表2 D-H参数取值范围
根据该模型得到的变换矩阵如下:
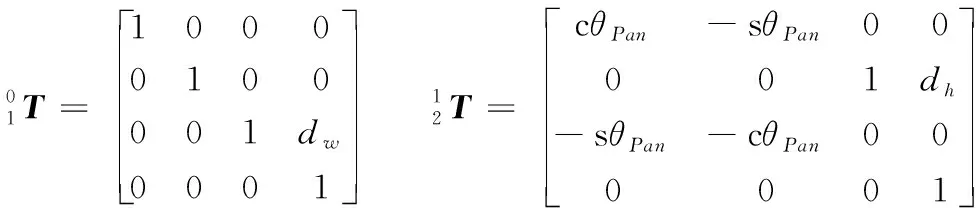

(1)
其中,O4(x4,y4,z4)为第4坐标系相对于初始坐标系的原点,同时是摄像机拍摄位置的坐标。得到该位置坐标后即可进行反解。
2.3 工作末端位置
确定工作末端即确定在摄像机画面上选取的某一点的空间位置。平面内一点O4由式(1)确定,过该平面的法向量z4为:
若设z4=(A,B,C),O4(x4,y4,z4),该平面方程:
A(x-x4)+B(y-y4)+C(z-z4)=0
将拍摄到的画面描述为宽16i,高9i的长方形,i值可由镜头参数和当前镜头上的zoom编码器返回值确定。选取的点P即可用(θi,μi)表示。经过空间坐标系推导得P的坐标为:
(2)
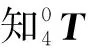
3 运动学反解算法验证

图4 从屏幕中取得空间点坐标
此改进的D-H算法将被拍摄物体作为工作末端,当控制dw、dh、θPan、θTilt时,摄影机器人工作末端即可达到焦距所达的任意位置,即可达到整个可拍摄空间;同时,对于空间内一点,有无穷多运动学反解,即无论需要拍摄哪一点,总有无穷多个机位可以拍摄到。实际使用中,行走和升降一般由操作人员主动控制,然后由云台自动控制摄像机对准所选中的物体。由于此算法和应用存在以上特殊情况,简单选取某坐标进行反解一定有无穷多解。所以验证时采用一个具体的使用情景:摄影机器人在轨道上由0处向6000mm处匀速运动,此时升降dh=1500mm,镜头聚焦df=5000mm处,θPan=180°、θTilt=90°。在行进至dw=1000mm处时选择屏幕左上角一点(i=100mm)。然后将云台调整至将摄像机对准该点,直至摄像机到达6000mm处。
根据建立的D-H连杆模型和式(2)求解屏幕左上角点位置。可得该点在空间中的实际坐标为(5000,1950,200),原有点O4、新点和所拍摄的画面位置如图4所示。
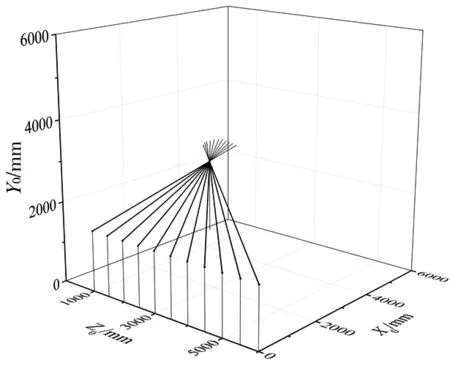
图5 行走过程求解
得到需要拍摄的点后,运用MATLAB软件编程可进行运动学逆解[10-12],其中P(5000,1950,200),dh为定值常量,dw为自变量;可求解θPan、θTilt。将行程中的解表现在图5中,为了图片直观清晰,只列出部分解在三维空间中的图示。图6为整个过程中θPan与θTilt随dw变化的函数图像。
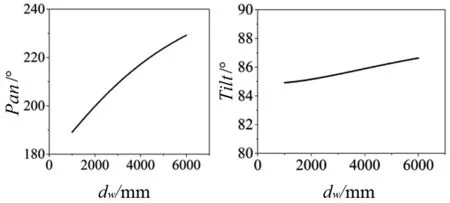
图6 两关节变化函数图像
在上例中没有改变升降dh的值,改变时可同理求解。在将dw、dh作为已知量求解时,θPan、θTilt在取值范围内只有有唯一解或无解两种情况。其中无解是由于摄像机俯仰角θTilt受到机械结构限制。

图7 摄影机器人实机
将此算法写入摄影机器人控制程序,通过实机对该算法进行试验验证。图7为摄影机器人实机。
测试时,先将设置摄影机器人在轨道上运行的速度和距离。开始运行后,单击屏幕上一点,观察摄影机器人在接下来的运动中回传的图像。为了保证测试具有说服力,分别使用表3的行走距离和行走速度互相组合进行35次跟踪拍摄,以第一次安装为基准,每种安装误差选用7次。

表3 测试参数
经试验验证,可以在不同速度和不同位移距离下完成跟踪拍摄,且安装误差对图像没有明显影响。图8为某次运行时回传的部分截取画面,其中被单击点为左侧门把手,运行距离为4000mm,行走运行速度为150mm/s。

图8 跟踪拍摄截取画面
综上所述,该算法可以完成屏幕上取点转换为空间点,和控制机器人在轨道上行走和升降并同时拍摄选中坐标点的要求,且不受安装误差影响。
4 结论
本文以虚拟演播室摄影机器人为研究对象,结合摄影机器人的特殊功能和使用习惯,提出了改进的D-H连杆法。将焦距扩展为虚拟连杆,通过自研镜头伺服器测得虚拟连杆的伸长度。
提出了可将三维空间位置从二维拍摄图像中提取出来的算法;摄影机器人在轨道上运动时,可以通过选
取屏幕中某点,控制PTZ云台对空间内该点进行自动跟踪拍摄。解决了摄影机器人控制的关键问题。
算法的反解坐标点不限于定点,也可以对空间内动点进行跟踪拍摄,如果结合视觉识别或人脸识别技术,即可完成对某一物体或主持人的跟踪拍摄。
通过在MATLAB软件上编程计算和摄影机器人实机上的试验,成功完成了对空间点的跟踪拍摄,验证了该算法的正确性。
[参考文献]
[1] Gibbs S,Arapis C,Breiteneder C,et al. Virtual studios: an overview[J]. IEEE Multimedia, 1998, 5(1):18-35.
[2] Wojdala A. Can virtual look real: a review of virtual studio techniques[C].Confluence of computer vision and computer graphics, 2000:229-252.
[3] Bernas M, Teisler M. Determination of the camera position in virtual studio[C].IEEE International Symposium on Signal Processing and Information Technology,IEEE, 2003:535-538.
[4] 蔡自兴.机器人学[M].北京:清华大学出版社,2015.
[5] 陈杨. 虚拟3D技术中摄像机云台姿态高精度测试方法研究[D].南京:南京理工大学,2016.
[6] 史艳琼. 变焦摄像机跟踪定位与测量技术[D].合肥: 合肥工业大学,2012.
[7] 鲁敏, 匡纲要, 郁文贤. 基于机械跟踪的虚拟演播室系统中摄像机校准和定位算法[J]. 国防科技大学学报, 2004, 26(3):68-73.
[8] Salvi J, Armangué X, Batlle J. A comparative review of camera calibrating methods with accuracy evaluation[J]. Pattern Recognition, 2002, 35(7):1617-1635.
[9] 克来格, 貟超. 机器人学导论[M].北京:机械工业出版社,2006.
[10] 汪永元. 工业机器人的系统分析与仿真研究[D].成都:西南交通大学,2014.
[11]韩建海, 吴斌芳, 杨萍, 等. 工业机器人[M].武汉:华中科技大学出版社, 2009.
[12]杨前明, 刘亚琼, 王伟,等. 基于D-H算法的棉桶更换复合机器人运动学建模与仿真分析[J]. 组合机床与自动化加工技术, 2016(12):52-55.

