具饱和发生率的被修正HIV传染病模型的全局稳定性*

杨俊仙，王雷宏

（1.安徽农业大学理学院，安徽合肥230036；2.安徽农业大学林学与园林学院，安徽合肥230036）

艾滋病的病原体是人类免疫缺陷病毒（Human Immunodeficiency Virus，简称 HIV），主要感染人体免疫系统细胞CD4＋T，可引起细胞计数大幅度下降，导致人体免疫缺陷，严重影响患者抵御感染的能力[1]。

目前，数学建模已经成为分析和控制传染病传播的重要工具。近年来，对艾滋病在数学建模方面的研究已取得很大进展[2-3]。对模型的改进是为了更好地分析和解释病情，并预测和控制发病率。最初的HIV/AIDS模型是由Nowak和Perelson等[4-5]提出的，该模型被广泛应用于艾滋病感染动力学：

其中T（t），I（t），V（t）分别表示t时刻未感染 CD4＋T细胞个数、已感染CD4＋T细胞个数和病毒载量（HIV）。参数A表示未感染细胞的固有生成率，β表示病毒感染率，d1，d2，d3分别表示未感染细胞、已感染细胞和病毒的死亡率，k表示病毒复制率。A，β，d1，d2，d3，k均为正数。

在20世纪90年代，有一个关于HIV RNA转录成DNA的讨论：当HIV病毒进入CD4＋T细胞后，HIV病毒可能并未完全反转录成DNA。在病毒基因组被整合到淋巴细胞基因组之前，一部分处于潜伏期的感染细胞可以恢复到未被感染的状态[6]。最近，已有一些数学模型建立在这样假设（部分感染细胞可恢复到未被感染状态）的基础上[7-8]。其中 Srivastava和 Chandra讨论了如下模型[7]：

其中变量T（t），I（t），V（t）和参数A，β，d1，d2，d3，k与模型（1）具有相同的意义，这里参数p（p＞0）表示处于潜伏期感染细胞的恢复率。

在模型（1）和（2）中，感染率 βT（t）V（t）被假设为在未感染细胞个数T（t）和病毒载量V（t）之间是双线性的。然而，实际发生率可能不是完全双线性的。Sun等[9]提出了如下模型：

此处用的是非线性发生率即发生率不再是未感染细胞个数T（t）和病毒载量V（t）的双线性关系。

在本文，我们提出了具有饱和发生率的被修正HIV传染病模型：

假设参数α＞0且d1≤d2。

由系统（4）的前2个方程得，

再由系统（4）的第3个方程得

于是

因此系统（4）的正向不变集为

1 平衡点的局部稳定性

系统（4）总存在无病平衡点E0（T0，0，0），其中。定义基本再生数

易证：当R0＞1时，系统（4）存在唯一的正平衡点E*（T*，I*，V*），其中

且正平衡点E*（T*，I*，V*）在Ω的内部：

因此，只需要在Ω0上考虑E*（T*，I*，V*）的稳定性。

1.1 无病平衡点E0的局部稳定性

定理1当R0＜1时，系统（4）的无病平衡点E0（T0，0，0）是局部渐近稳定的；当R0＞1时，E0（T0，0，0）是不稳定的。

证明系统（4）在无病平衡点E0（T0，0，0）处的线性化系统的特征方程为

显然，方程（9）总有负实根λ＝-d1，其余的根取决于方程

整理方程（10）得

当，方程（11）所有的根均有负实部，因此无病平衡点E0是局部渐近稳定的。当R0＞1时，方程（11）有一个正实根，因此无病平衡点E0是不稳定的。

1.2 正平衡点E*（T*，I*，V*）的局部渐近稳定性

定理2当R0＞1时，系统（4）的正平衡点E*（T*，I*，V*）是局部渐近稳定的。

证明系统（4）在正平衡点E*（T*，I*，V*）的线性化系统的特征方程为

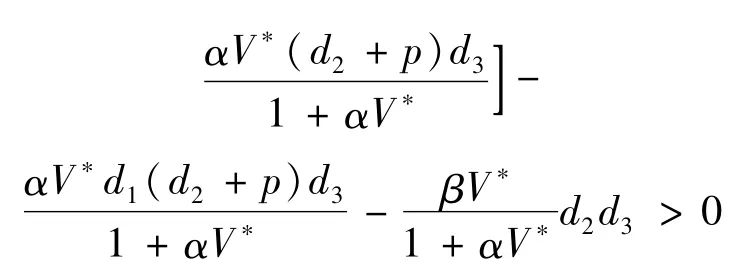
由Routh-Hurwitz判别准则知，正平衡点E*（T*，I*，V*）是局部渐近稳定的。

2 平衡点的全局稳定性

2.1 无病平衡点E0的全局渐近稳定性

定理3当R0＜1时，系统（4）的无病平衡点E0（T0，0，0）在Ω内是全局渐近稳定的。

证明令（T（t），I（t），V（t））是系统（4）的任一正解，定义Lyapunov函数：

计算V1（t）沿系统（4）的全导数：

当R＜1时，当且仅当V（t）＝0时。因此，在 Ω内的最大正向不变集为

于是有极限方程：

定义Lyapunov函数：

其中T0＝。计算V2（t）沿系统（13）的全导数：

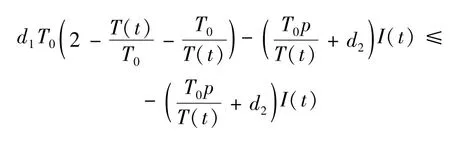
其中当且仅当T（t）＝T0，I（t）因此的正向不变集为：

由 LaSalle不变集原理知，E0（T0，0，0）是全局渐近稳定的。

2.2 正平衡点E*的全局渐近稳定性

设开集是C1函数。考虑微分方程

设x（t，x0）代表方程（15）满足条件x（0）＝x0的解。令是系统（15）的一个平衡点，Li等[10]作了下面两个基本假设：

（H1）方程（15）在Γ内存在一个紧吸引子集K⊂Γ；

（H2）方程（15）在Γ内有唯一平衡点∈Γ。

给出了如下结论：

引理1[10]若下列条件成立：

（i）假设（H1）和（H2）成立；

（ii）方程（15）满足 Poincare′-Bendixson性质；

（iii）对系统（15）具有p（0）∈D的每一个周期解x＝p（t），系统（15）关于p（t）的二阶复合矩阵

是渐近稳定的，其中是f的Jacobian矩阵的第二加性复合矩阵；

则系统（15）的唯一平衡点在Γ内是全局渐近稳定的。

定理4当R0＞1时，系统（4）的正平衡点E*（T*，I*，V*）在Ω0内是全局渐近稳定的。

证明根据引理，逐条验证四个条件：

（i）条件（H1）等价于系统（4）的一致持久性[11]。由式（8）知，Ω0是有界的，所以对于系统（4）的一致持久性的充分必要条件等价于平衡点E0是不稳定的 。定理1已证：当R0＞1时，E0是不稳定的，因此系统（4）一致持久的，从而（H1）成立。

同时，由于E*（T*，I*，V*）是系统（4）在Ω0内的唯一平衡点，因此（H2）成立。

（ii）系统（4）的Jacobian矩阵为

取H＝diag（1，-1，1），则

显然，HJH的非对角线元素非正，系统（4）满足Poincare′-Bendixson性质，因此引理1的条件（ii）成立。

（iii）令p（t）＝（T（t），I（t），V（t））是系 统（4）在Ω0内的任意一个周期解，则系统（4）的Jacobian矩阵的第二加性复合矩阵为

沿系统（4）任一周期解（T（t），I（t），V（t））的二阶复合系统为

考虑Lyapunov函数：

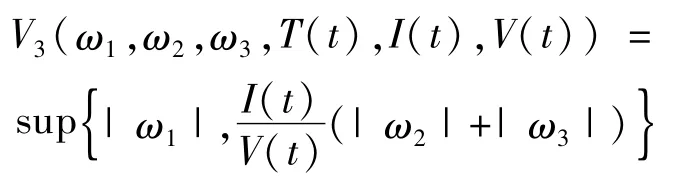
由一致持久性知，周期解p（t）＝（T（t），I（t），V（t））与边界∂Ω有一定的距离，故存在常数μ＞0，使得T（t）＞μ，I（t）＞μ，V（t）＞μ。并结合式（8）中的得

对全部（ω1，ω2，ω3）∈ R3及（T（t），I（t），V（t）），计算V3的右导数。注意到

于是由式（22），式（25）和Gronwall不等式得

由上式知故由式（19）知，当t即二阶复合系统（18）是渐近稳定的。这样就验证了引理1中的条件（iii）。

（iv）由式（13）可得，

由于J（E*）是3×3矩阵，即n＝3，于是

验证了引理1的条件（iv）。

因此，当R0＞1时，由引理得，系统（4）唯一的正平衡点E*（T*，I*，V*）在Ω0内是全局渐近稳定的。

3 数值模拟

在系统（4）中，令参数A＝5，k＝10，β＝0.000 2，α＝0.5，p＝0.5，d1＝0.1，d2＝0.5，d3＝0.3，显然R0＝＜1，此时系统存在一个无病平衡点E0（50，0，0）。由定理3可知，E0是全局渐近稳定的，数值模拟结果验证了上述结论（见图1）。

图1 R0 ＜1时，E0（T0，0，0）的稳定性Fig.1 When R0 ＜1，the stability of E0（T0，0，0）

若令参数此时系统（4）有唯一的正平衡点E*（41.92，1.62，53.89）。根据定理4可知，E*是全局渐近稳定的，数值模拟的结果与文中结论一致（见图2）。

图2 R0＞1时，E*（T*，I*，V*）的稳定性Fig.2 When R0 ＞1，the stability of E*（T*，I*，V*）

[1]WANGL C，LI M Y.Mathematical analysis of the global dynamics of a model for HIV infection of CD4＋T cells[J].Mathematical Biosciences，2006，200（1）：44-57.

[2]杨俊仙，吴元翠，闫萍.一类具时滞与饱和发生率的HIV-1传染病模型的全局稳定性[J].中山大学学报（自然科学版），2016，55（4）：26-29，38.YANG J X，WU Y C，YAN P.Global stability of a HIV-1 epidemic model with time delay and saturation incidence rate[J].Acta Scientirum Naturalium Universitatis Sunyatseni，2016，55（4）：26-29，38.

[3]冯依虎，陈贤峰，莫嘉琪.一类免疫缺陷病毒传播的非线性动力学系统[J].中山大学学报（自然科学版），2017，56（5）：60-63.FENG Y H，CHEN X F，MOJQ.A class of nonlinear dynamic system of human groups for HIV transmission[J].Acta Scientirum Naturalium Universitatis Sunyatseni，2017，56（5）：60-63.

[4]NOWAK M A，BANGHAM CR M.Population dynamics of immune responses to persistent viruses[J].Science，1996，272（5258）：74-79.

[5]PERELSON A S，NELSON P W.Mathematical models of HIV dynamics in vivo[J].SIAM Review，1999，41（1）：3-44.

[6]ESSUNGER P，PERELSON A S.Modeling HIV infection of CD4＋T cell subpopulations[J].Journal of Theoretical Biology，1994，170（4）：367-391.

[7]SRIVASTAVA PK，CHANDRA P.Modeling the dynamics of HIV and CD4＋T cells during primary infection[J].Nonlinear Analysis： Real World Applications，2010，11（2）：612-618.

[8]BUONOMO B，VARGAS-DE-LEON C.Global stability for an HIV-1 infection model including an eclipse stage of infected cells[J].Journal of Mathematical Analysis and Applications，2012，385（2）：709-720.

[9]SUN Q L，MIN L Q.Dynamics analysis and simulation of a modified HIV infection model with a saturated infection rate[J].Computational and Mathematical Methods in Medicine，2014，2014（5258）：145162.

[10]MICHAEL Y L，WANG L C.Global stability in some SEIR epidemic models[J].Mathematical Approaches for Emerging and Reemerging Infectious Diseases：Models，Methods，and Theory，2002，126：295-311.

[11]WALTMAN P.A brief survey of persistence[C]∥Proceedings of a Conference in Honor of Kenneth Cooke，1991：31-40.

[12]LI M Y，GRAEF JR，WANG L，et al.Global dynamics of a SEIR model with varying total population size[J].Mathematical Biosciences，1999，160（2）：191-213.