复多项式微分系统的广义中心问题和可积性*
郭珂珂,张齐
(中南大学数学与统计学院,湖南长沙410083)
经典的平面多项式微分系统
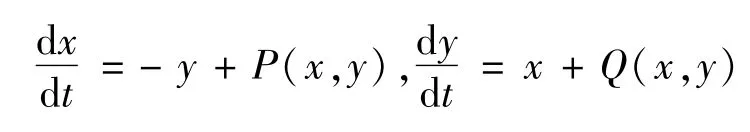
的中心问题是寻找P(x,y)和Q(x,y)的系数满足的条件,使原点的邻域由系统的周期解覆盖。关于该问题的研究仅在P(x,y)和Q(x,y)为二次和三次齐次多项式的情况下分别由Dulac与Sibirskii解决。在P(x,y)和Q(x,y)的其它情形一直是悬而未决的公开问题。但其中不乏优秀的成果[1-3]。与中心问题密切相关的是平面多项式微分系统的积分问题。
最近,文[4]把经典的中心问题推广到p:-q共振的情形:

寻找p:-q共振中心必要条件通常有两种方法。第一种是形式级数法,即逐项确定假设的形式首次积分H(x,y)=xqyp+…的泰勒展开式的各项,使
此形式首次积分存在的必要条件是由形式级数定义的各阶鞍点量gk为零。用此方法判断原点是否为共振中心涉及到鞍点量gk的计算。另一种方法是规范形法,它需要计算由规范形定义的所谓的广义奇点量[5-6]。
关于共振奇点广义中心条件的研究有不少有趣的工作。当P(x,y)和Q(x,y)是特殊的实或复多项式且共振比p:-q是特定的值时,系统存在局部解析首次积分H(x,y)=xqyp+…(即存在p:-q共振中心)的条件已有不少的研究。二次多项式的情形有文[4-13];三次的情形有文[14-20];四次情形有文[21-22];五次情形有文[23]。但是当共振比是一般的值时,即使是二次系统,共振中心问题仍然是一个公开问题。
值得一提的是,在文[5]中,肖和刘提出了一种比较容易的计算鞍点量的方法(在文[5]中称为广义奇点量)。他们考虑了以下一般的复自治微分系统

其中z,w,T是独立的复变量,aαβ,bαβ是复常数,p,q∈Z+,(p,q)=1。作者通过系统(1)的规范形给出了广义奇点量的定义,并运用形式级数,得到了一个计算鞍点量的线性递归公式。但是,文[5]有一个缺陷,作者直接将从形式级数得到的鞍点量作为从规范形定义的广义奇点量,而没有证明它们的等价性。因此本文的其中一个目的就是填补这个空缺。我们首先证明了广义奇点量和鞍点量的等价性,换句话说,证明了形式级数法和规范形法的等价性。然后引入一种计算广义共振奇点量的方法—积分因子法,并由此判定广义中心。我们还得到了计算系统(1)原点的广义奇点量的另一递归公式。
1 预备知识
引理1[5,7]对于系统(1),我们可以逐项确定以下形式级数

使系统(1)转换成其规范形:
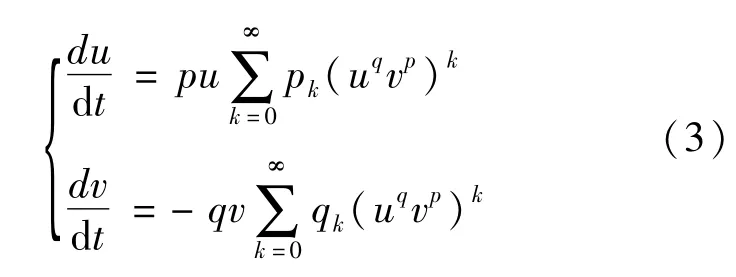
其中p0=q0=1.
设H=uqvp,μk=pk-qk,那么由规范形(3)可得

定义1[5-6]对于系统(1),我们称 μk=pkqk为 “原点的第k阶广义奇点量”。如果μ1=μ2=…=μk-1=0,μk≠0,则原点称为k阶奇点;如果对所有k都有μk=0,则原点称为复共振中心。
注1有些作者也把广义奇点量称为鞍点量[7,11]。为了区别由形式级数法和规范形法得到的鞍点量,本文采用文[5]中方法把由规范形法得到的鞍点量称为广义奇点量。
定理1[5]对于系统(1),可以逐项确定以下形式级数

使得

其中cqp=1,ckq,kp=0,k=2,3,….当 α+β>p+q,且qβ-pα≠0时有

2 主要结果
定理2对于系数为系统(1)的系数aαβ,bαβ的多项式的任意形式级数

以及任意预先给定的ckq,kp(k=1,2,…),可以逐项确定唯一的形式级数
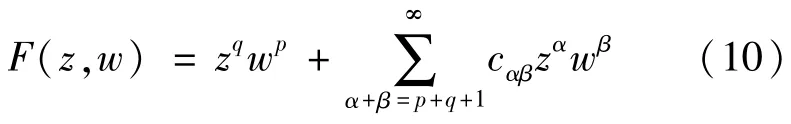
使其系数也是aαβ,bαβ的多项式,且
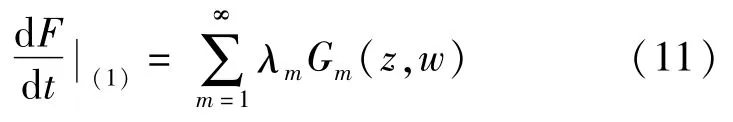
此外,如果μ1=μ2=…=μk-1=0,μk≠0,则λ1

反之亦然。
证明定理的前半部分和式(11)通过直接计算很容易证明,在此从略。现证明另一半和式(12)。运用形式级数(2),F(z,w)和Gm(z,w)可以写成

其中的子序列,因而是Gm中含有某些特殊项的部分。因为H=uqvp,我们也可以简化式(14)为

其中gm(H)是H的幂级数,且gm(0)=1。此外,由规范形(3)和等式(13)可得

另一方面,由形式级数(2)和式(11),又可得
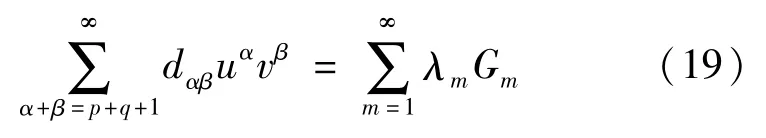
因此,

综合式(18)与式(20)得

由式(21)可知:如果μ1=μ2=…=μk-1=0,μk≠0,则有 λ1=λ2=…=λk-1=0,λk≠0,且式(12)成立。
定理2从理论上证实了:除了可能相差一个常数因子外,由定理1通过形式级数法得到的鞍点量恰是系统(1)原点的广义奇点量。
推论1系统(1)在原点可积,从而存在一个解析的首次积分,当且仅当原点是广义中心。
定理3对于系统(1),我们可以逐项确定以下形式级数

其中系数是系统(1)的系数aαβ,bαβ的多项式,(k=1,2,…)可任取,且
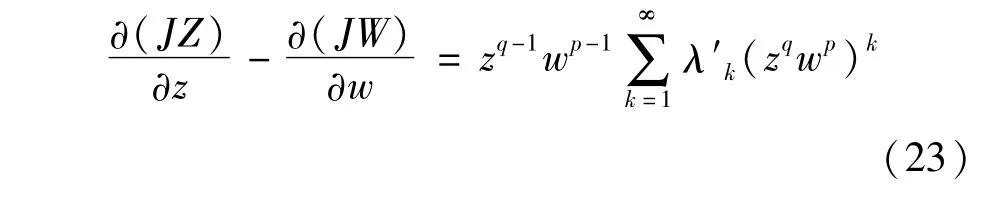
此外,如果μ1=μ2=…=μk-1=0,μk≠0,则有
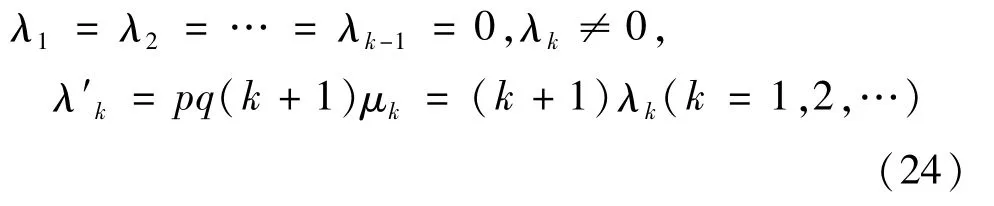
反之亦然。
证明我们将在下一个定理中详细证明J(z,w)的存在。首先证明式(24)成立。
令

由式(23)和式(25)可得

因而再有式(25)-(26)可知,存在一个形式幂级数F=zqwp+…,使得

由式(27),做形式计算可得

其中

由定理2,式(28)-(29)易得如果μ1=μ2=…=μk-1=0,μk≠0,则,且式(24)成立。
定理4对系统(1),可以逐项确定形式级数(22),使等式(23)-(24)成立。此外,若pα=qβ,可任取;若pα≠qβ,且=1,则当m≥1时有

其中当k<0或j<0时,akj=bkj=ckj=0.
证明将Z,W表示为

则有

如果pα≠qβ,则易由式(33)得到式(30);如果pα=qβ,则存在一个正整数m≥1,其中α=qm,β=pm,此时等式(23)-(30)也成立。
注2定理2-4不仅揭示了鞍点量与广义奇点量之间的关系,而且揭示了计算广义奇点量的首次积分法,积分因子法和规范形法3种计算方法的等价性。系统(1)原点的广义奇点量除了常数因子之外是唯一确定的。因此,不失一般性,我们可以用 λk和代替 μk。
推论2系统(1)的原点是广义中心当且仅当它有解析的积分因子。
3 应用举例
考虑如下以原点为共振奇点的复多项式系统

使用公式(30)-(31)计算系统(34)原点的广义奇点量,可得
命题1系统(34)原点的前2个广义奇点量是

其中


定理5原点的前两个广义奇点量均为零当且仅当下列条件之一成立
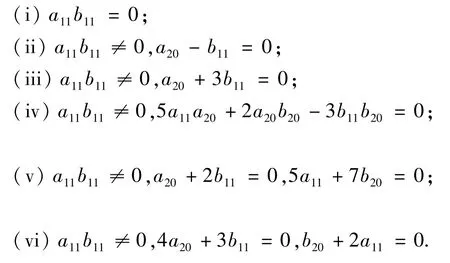
证明只要将六个条件中的任一个代入前2个广义奇点量,就可证明充分性。现证必要性。对于这六个条件,前4个是从μ1,μ2表达中显而易见的。所以我们只需证明后2个。如果μ1=μ2=0,除前4个条件外,必有H1=H2=0。令S=[H1,H2,a11],则有

如果H1=H2=0必有S=0。由H1=H2=0和S=0我们进一步可得式(5)和式(6)以及包含在式(4)中的其他特殊结果。
从文[6]中的定理3.2和定理4.1可得
命题2系统(34)的原点是一个广义中心(即,系统(34)在原点可积)当且仅当定理5中的六个条件之一成立。
注3在命题2中得到的广义中心条件与文[9]中的定理4.1的条件一致,这证实了本文中建立的理论和公式的正确性。
[1]黄文韬,刘一戎,朱芳来.一类微分系统无穷远点的中心与拟等时中心[J].中山大学学报(自然科学版),2005,44(4):24-27.HUANG W T,LIU Y R,ZHU F L.The centers and quasi-isochronous centers at infinity for a class of differential systems[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2005,44(4):24-27.
[2]李时敏.一类不连续广义Lienard微分系统的极限环分支[J].中山大学学报(自然科学版),2015,54(5):15-18,27.LI SM.Bifurcation of limit cycles for a class of discontinuous generalized Lienard differential system[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2015,54(5):15-18,27.
[3]黄赪彪,邬华东.平面二次系统极限环及其稳定与分岔的计算[J].中山大学学报(自然科学版),2008,47(2):28-31.HUANG C B,WU H D.Calculation of limit cycles and their stability and bifurcations for planar quadratic differential systems[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2008,47(2):28-31.
[4]ZOLADEK H.The problem of center for resonant singular points of polynomial vector fields[J].J Differential E-quations,1997,137(1):94-118.
[5]XIAO P.Critical point quantities and integrability conditions for complex planar resonant polynomial differential systems[D].Changsha:Central South University,2005.
[6]WANG Q,LIU Y.Linearizability of the polynomial differential systems with a resonant singular point[J].Bull Sci Math,2008,132(2):97-111.
[7]GRAVEL S,THIBAULT P.Integrability and linearizability of the Lotka-Volterra system with a saddle point with rational hyperbolicity ratio[J].J Differential Equations,2002,184(1):20-47.
[8]FRONVILLE A,SADOVSKI A,ZOLADEK H.Solution of the1:-2 resonant center problem in the quadratic case[J].Fund Math,1998,157(2/3):191-207.
[9]LIU C,CHEN G,LI C.Integrability and linearizability of the Lotka-Volterra systems[J].J Differential Equations,2004,198(2):301-320.
[10]CHRISTOPHER C,ROUSSEAU C.Normalizable,integrable and linearizable saddle points in the Lotka-Volter-ra system[J].Qual Theory Dyn Syst,2004,5(1):11-61.
[11]CHRISTOPHER C,MARDEŠP,ROUSSEAU C.Normalizable,integrable and linerizable saddle points for complex quadratic systems inC2[J].J Dyn Control Syst,2003,9(3):311-363.
[12]WANG Q,HUANG W.Integrability and linearizability for Lotka-Volterra systems with the 3:-qresonant saddle point[J].Adv Difference Equ,2014,2014(1):23.
[13]FERĈECB,GINÉJ,MENCINGER M,et al.The center problem for a 1:-4 resonant quadratic system[J].J Math Anal Appl,2014,420(2):1568-1591.
[14]DOLIĈANIN D,GINÉJ,OLIVEIRA R,et al.The center problem for a 2:-3 resonant cubic Lotka-Volterra system[J].Appl Math Comput,2013,220(4):12-19.
[15]WANGQ,HUANGW,WU H.Linear recursion formulas of generalized focus quantities and applications[J].Appl Math Comput,2013,219(10):5233-5240.
[16]GINÉJ,CHRISTOPHER C,PREŠERN M,et al.The resonant center problem for a 2:-3 resonant cubic Lotka-Volterra system[M]//Computer Algebra in Scientific Computing.Berlin Heidelberg:Springer,2012,7442(4):129-142.
[17]LIU C,LIY.The integrability of a class of cubic Lotka-Volterra system[J].Nonlinear Anal Real World Appl,2014,19(19):67-74.
[18]HU Z,ROMANOVSKI V,SHAFER D.1:-3 resonant centers onC2with homogeneous cubic nonlinearities[J].Comput Math Appl,2008,56(8):1927-1940.
[19]CHEN X,GINÉJ,ROMANOVSKI V,et al.The1:-qresonant center problem for certain cubic Lotka-Volterra system[J].Appl Math Comput,2012,218(23):11620-11633.
[20]WANG Q,WU H.Integrability and linearizability for a class of cubic Kolmogorov systems[J].Ann Differential Equations,2010,26(4):442-449.
[21]DONG G.Linearizability of homogeneous quartic polynomial systems with 1:-2 resonance[J].JMath Anal Appl,2012,396(1):215-224.
[22]LIU C,CHEN G,CHEN G.Integrability of Lotka-Volterra type systems of degree 4[J].J Math Anal Appl,2012,388(2):1107-1116.
[23]GINÉJ,ROMANOVSKI V.Integrability conditions for Lotka-Volterra planar complex quintic systems[J].Nonlinear Anal Real World Appl,2010,11(3):2100-2105.

