车辆双磁流变阻尼器座椅悬架的建模及控制

赵 强，赵吉业，张 娜

(东北林业大学 交通学院， 哈尔滨 150040)

悬架是车辆中关系到车辆平顺性、操控稳定性等性能的重要总成[1]。传统的参数固定的被动悬架不能实时调节，因而路面适应能力差。近20年来，随着技术的进步和汽车产销量的增加，主动悬架、半主动悬架技术的成本逐步降低，应用日益广泛。半主动悬架由于制造和运行成本都低于主动悬架且可取得较接近于主动悬架的性能而日益受到关注[2]。

磁流变半主动悬架不需要高压激励电源，易于在实车上实现，因而具有较好的应用前景。目前在磁流变半主动悬架的控制方面采用的方法包括模糊控制[3-4]、最优控制[5]、预瞄控制等[6]。

半主动悬架设计中的变刚度变阻尼结构方案采用多磁流变阻尼器并联的新型减振结构[7-9]，具有较好的减振性能。本文研究将双磁流变阻尼器应用于车辆座椅-人体的减振方面，为其建立基于分层控制的控制算法，并通过仿真验证其有效性。

1 磁流变半主动悬架模型

1.1 半主动悬架模型

一般的单自由度振动系统(见图1(a))可以通过在激励源(x0)和振动质量m2之间的弹簧上串联加入附加质量m1和Vogit单元(k2∥c2)实现动力吸振，其结构如图1(b)所示。带附加质量和Vogit单元的单自由度振动系统通过m1消耗振动能量，因此具有较好的隔振效果，但是其对频率位于由m1和k1与k2形成的频点及其附近处的激励的隔振效果较差。目前提出的双磁流变阻尼器方法是将固定阻尼的c1和c2都用可调的磁流变阻尼器代替，通过调节它们可以实现可变刚度和阻尼，从而改变上述频点处的隔振效果。本文基于上述思想在车辆座椅悬架上采用双磁流变阻尼器，以提高座椅减振效果，具体做法为：考虑到2自由度被动的车辆座椅-人体的振动系统如图2所示，阻尼器c1和c3不可调节，是典型的被动振动系统，将c1替换为新的可调的磁流变阻尼器c1；将弹簧k2和磁流变阻尼器c2并联构成Vogit单元，并在其下附加调节质量m1，m1进一步通过弹簧k1与激励x0相连。最后形成的3自由度半主动悬架如图3(a)所示，其通过调节c2可以改变右侧k1-m1-(k2∥c2)支链的等效刚度，而调节左侧c1可改变阻尼，从而实现变刚度和变阻尼的有效隔振。上述方案在“剪式”座椅悬架上的具体实现结构见图3(b)，由于所研究座椅悬架应用于重卡等车辆，故其提供的安装空间较大，能满足空间要求。另外，增加的质量m1相对较小，只对提高座椅减振性能起作用，不影响整车性能。

图1 单自由度振动系统

图2 被动悬架系统

图3 双磁流变半主动悬架系统

采用牛顿第二定律建立图2所示的被动悬架和图3所示的半主动悬架系统的运动微分方程分别如下：

(1)

(2)

(3)

(4)

(5)

式中：m1、m2、m3分别为图2、3中同名称的各物体的对应质量，类似地，c1、c2、c3为对应阻尼，k1、k2、k3为对应的弹簧刚度；x0为座椅底部输入的激励位移；x1为调节质量的竖向位移；x2和x3分别为座椅和人体的竖向位移。

1.2 磁流变阻尼器模型

磁流变阻尼器通电后，磁流变液的动态本构关系呈现为强非线性关系，目前其建模方法分为理论建模方法和试验建模方法。理论推导出的Binham模型和Herschel-Bulkey模型能较精确地反映力位移特性，适用于磁流变阻尼器设计计算中的力求解。Spencer等[10]采用试验方法建立了磁流变阻尼器的现象模型，在原Bouc-Wen滞环模型的基础上加入低、高速时的阻尼元件、刚度元件。该模型较准确地反映了低速时速度-力之间的非线性磁滞特性,与实测结果比较吻合,因此明显优于其他参数化模型，适用于磁流变阻尼器的精确控制。根据文献[10]建立的改进Bouc-Wen模型具体如图4所示，其中：k1为磁流变阻尼器底部所充氮气形成的刚度；y为弹簧的初始位移；弹簧k0用来控制高速时的刚度；c0为高速阶段黏滞阻尼元件；c1为低速阶段黏性元件，用来产生力-速度关系中低速时的非线性衰减。

对应于图4的物理模型，得到磁流变阻尼器的总阻尼力为

(6)

式中：y为中间位移变量，其1阶导数为

(7)

(8)

式(6)～(8)中的β、γ、αa、αb、c0a、c0b、c1a、c1b、A、k1、k0、x0、n、η均为固定参数，共14个，可通过实验辨识得到，即按照实测的磁流变阻尼器位移-力曲线、速度-力曲线采用最小二乘法等方法辨识出以上参数。Spencer等给出的参数取值使改进模型在该模型的各个区域尤其是描述非线性磁滞特性方面都能与实验数据基本吻合。

图4 改进Bouc-Wen模型

2 分层控制策略

本文采用分层控制策略，如图5所示。上层采用基于模型的控制算法，根据半主动悬架机构的动力学方程解算出系统需要2个阻尼器提供的计算阻尼力。下层为磁流变阻尼器的控制算法，在上层解算出的计算阻尼力基础上增加根据座椅位移和速度得到的PD控制补偿项，所得结果即2个磁流变阻尼器需要输出的期望阻尼力。将这2个期望阻尼力信号输出给每个磁流变阻尼器的阻尼力控制器，进一步由阻尼力控制器采用阻尼力控制策略解算出需要的控制电压，输出给磁流变阻尼器，从而使其产生相应的阻尼力实现减振。

图5 磁流变座椅控制系统

上层的计算模型控制器根据式(3)～(5)确定计算阻尼力值，确定磁流变阻尼器1和2应输出的计算阻尼力分别为：

Fb1=-k2(x2-x1)-Fr2

(9)

Fb2=-k2(x2-x1)-Fr1

(10)

式中：Fr1和Fr2分别为2个磁流变阻尼器的实际出力。

2个阻尼器都根据座椅位移和速度计算PD控制项作为补偿，补偿项为

(11)

式中：kp为比例系数；TD为微分时间常数。

2个阻尼器的期望阻尼力分别为：

Fd1=-k2(x2-x1)-Fr2+

(12)

Fd2=-k2(x2-x1)-Fr1+

(13)

磁流变阻尼器控制器接受上述期望阻尼力并进一步采用如下开关型非连续控制算法计算控制电压：

i=1,2

(14)

3 仿真试验

基于上述模型和控制算法在Simulink中搭建双磁流变座椅及其控制系统的仿真框图，见图6。为了与固定阻尼的被动减振方法进行对比，在图7中给出了被动座椅悬架的仿真框图，图7中的座椅悬架的结构和图6相同，但2个阻尼器都选用固定值。

图6 磁流变座椅分层控制仿真框图

图7 磁流变座椅在被动减振下的仿真框图

首先取正弦信号作为激振信号。考虑到人体的敏感频率区间为8～12 Hz，这里的激振分别取8、10和12 Hz的正弦信号进行测试，振幅均取0.01 m，仿真参数设置：m1、m2、m3分别为20、30、75 kg；k1、k2、k3分别为5 000、5 000、75 500 N/m；c3为3 840 N·S/m,c1、c2均为5 000 N·S/m(被动减振)；λ=0.1,kp=100；TD=10。 仿真时采用变步长的ode32t进行求解，仿真结果参见图8～10。

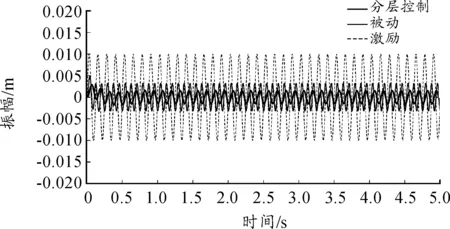
图8 频率8 Hz下的振动响应

图9 频率10 Hz下的振动响应

图10 频率12 Hz下的振动响应

由图8～10可知：在以上3种频率下，对于振幅0.01 m的正弦激励，采用被动减振方式的座椅的输出振幅在0.004 9～0.005 5 m；而采用半主动的分层控制方式时，座椅的振动幅值在0.001 4～0.001 6 m，相对被动减振情况，幅值衰减达到70%左右，效果比较明显。由于正弦激励是单一频率信号，所以通过控制算法实时调节2个磁流变减振器可以使悬架频率成功避开激振频率并使阻尼达到最佳。另外，若进一步采用优化算法对参数取值进行优化，预计能达到更好的效果。

进一步利用白噪声产生随机激励测试半主动座椅悬架在复合频率激励下的减振效果。采用 Simulink 中的 band-limited white noise 模块经过滤波产生 的200 Hz 以内的白噪声激励作为输入，得到磁流变座椅的时域响应，如图11(a)所示。由图11(a)可知：在随机激励下，分层控制的半主动座椅振幅比被动悬架振幅降低10%以上，说明在含各种频率成分的随机激励下，分层控制方法的减振效果依然很明显。采用傅里叶变换得到随机激励响应的频谱曲线，如图11(b)所示，由图可知：座椅采用分层控制时位移功率谱密度明显低于被动悬架，对振动能量实现了大幅度的衰减，减振效果明显。

图11 随机激励下的振动响应

4 结束语

本文建立了一种新型磁流变半主动座椅悬架模型，采用2个磁流变阻尼器，通过包括磁流变阻尼器的Vogit单元和调节质量、弹簧串联形成的支链以及另外的磁流变阻尼器并联构成座椅减振悬架。采用分层控制策略进行减振控制。正弦激励仿真测试结果表明，在人体振动敏感的8～12 Hz频率区域内，该半主动悬架采用分层控制策略相对于被动座椅悬架的减振效果非常明显，幅值衰减达到70%左右。采用随机激励的仿真测试结果表明，在复合频率激励下的半主动悬架相对被动悬架的减振效果仍能提高10%以上，表现出较好的减振性能。

[1] 赵向阳，侯锁军.磁流变减振器的整车操稳性试验研究[J].机床与液压,2016,44(5):109-111.

[2] 曾谊晖，周育才，刘道才，等.履带车半主动悬架的复合控制策略研究[J].中国机械工程,2013,24(8):1090-1096.

[3] 赵强，张娜.基于半车解耦的半主动悬架模糊滑模控制[J].噪声与振动控制,2016,10(5):59-64.

[4] 颜文俊,董丹,王维锐,等.非线性半主动悬架系统模糊控制策略[J].控制工程,2011,18(6):941-946.

[5] 王健，祖广浩.磁流变半主动悬架的史密斯预估-LQG 时滞补偿控制方法[J].重庆理工大学学报 (自然科学),2017,31(8):65-72,80.

[6] 邹斌，熊辉，李超群，等.基于Simulink/CarSim的磁流变悬架预瞄模糊控制[J].自动化与仪表，2017,32(12):61-67.

[7] LIU Y,MATSUHISA H,UTSUNO H,et al.Vibration isolation by a variable stiffness and damping system[J].International Journal of Japan Society of Mechanical Engineering,2005,48 (2):305-310.

[8] 范方强，潘公宇.变刚度和阻尼半主动悬架的模糊控制研究[J].重庆交通大学学报(自然科学版),2012,31(3):482-485.

[9] POTTER J N,NEILD S A,WAGG D J.Quasi-active suspension design using magnetorheo logical dampers[J].Journal of Sound and Vibration,2011,330:2201-2219.

[10] SPENCER Jr B F,DYKE S J,SAIN M K,et al.Phenomenological model of a magnetorheo logical damper[J].ASCEJournal of Engineering Mechanics,1996(3):1-23.