主动转向系统的变传动比设计及电机控制研究
李志鹏,单长伟,那少聃,奚文龙
(东北林业大学 a.交通学院; b.机电工程学院, 哈尔滨 150040)
转向系统是车辆操纵系统的核心,其性能直接影响到车辆的操纵稳定性和行车安全性。传统转向系统采用的是固定传动比,使得车辆在低速时转向不够灵敏,高速时转向稳定性较差。主动转向系统(active front steering,AFS)能实现变传动比转向,使车辆在低速转弯时采用小传动比,高速转弯时采用大传动比,解决了传统转向系统“轻”与“灵”的矛盾,提高了车辆的操纵稳定性。近几年,随着传感器技术及现代控制理论的发展,AFS控制技术成为当前汽车领域研究的热点[1]。
AFS变传动比曲线的设计主要是研究车速与转向传动比的关系。对此,国内外学者进行了大量的研究。文献[2]提出在固定稳态转向系统增益(车辆横摆角速度与方向盘角位移的比值)的基础上设计变传动比曲线,并且传动比是一个随车速变化的值。文献[3-4]采用了传统变传动比曲线(在中速段采用基于固定稳态转向系统增益的变传动比曲线,在低、高速段采用定传动比曲线),并以此来设计AFS转角电机的角位移信号,但是该变传动比曲线会造成转角电机加速度波动,冲击齿轮机构,影响其使用寿命。文献[5]运用模糊控制和固定转向系统增益两种方法来设计变传动比曲线,车辆在低、高速时采用模糊控制设计的变传动比曲线,中速时采用基于固定稳态转向系统增益设计的变传动比曲线。但这种方法并没有改善电机角速度波动大的问题。文献[6]提出了用改进型S函数整体拟合传统变传动比曲线,减小了转角电机的角加速度波动。但是这种整体拟合方法使得中速段的稳态转向系统增益波动较大,影响车辆的操纵稳定性。
针对以上研究的弊端,本文首先采用考虑等效侧倾效应的二自由度(侧偏与横摆)整车运动模型,设计基于固定稳态增益的变传动比曲线,然后构造反正切函数,运用最小二乘法对基于固定稳态增益的变传动比曲线局部拟合(中速段)。为实现对本文设计的转角电机角位移信号快速、准确跟踪,又设计了全局快速Terminal滑模鲁棒控制器。最后,通过仿真实验验证了拟合变传动曲线的性能和滑模控制算法的有效性。
1 系统模型
1.1 变传动比机构模型
AFS主要由变传动比齿轮机构、电磁锁止单元、电子控制系统、蜗轮蜗杆减速机构、转角电机等组成。采用双行星齿轮机构作为本文研究的变传动比机构,具体结构如图1所示。

1.蜗杆;2.蜗轮;3.上排行星轮系行星轮;4.上排行星轮系太阳轮;5.转向输入轴;6、11.行星轮系行星架;7.下排行星轮系内齿圈;8.下排行星轮系行星轮;9.下排行星轮系太阳轮;10.转向输出轴;12.上排行星轮系内齿圈
图1 双行星齿轮机构结构
双行星齿轮机构的上排行星轮系外齿圈为蜗轮,下排行星轮系的外齿圈固定,是一个二自由度的差动行星轮系。该机构有2个独立的主动件(转角电机、转向盘),可以实现2个独立运动的叠加。在车辆行驶的过程中,根据车速的不同,通过控制电磁锁止单元控制转角电机的启动与停止。当电磁锁止单元锁死时,AFS变为传统转向系统。当电磁锁止单元打开时,转角电机通过不同角度不同方向的旋转,能在转向盘转角的基础上改变车轮转角,达到变传动比的目的。
根据双行星齿轮机构的结构特点,得出其运动学模型:
(1)
(2)
整理式(1)(2)可得:
(3)
式中:θg为转角电机与方向盘到转向输出轴的叠加角;θd为转角电机转角;θs为方向盘转角;θdg为转角电机到转向输出轴的转角;θsg为转向盘到转向输出轴的转角;δ为前轮转向角;idg为转角电机到转向输出轴的传动比;isg为转向盘到转向输出轴的传动比;is为AFS传动比;im为小齿轮齿条传动比。
1.2 整车二自由度模型
考虑到车身侧倾对车辆运动的影响,Ellis提出考虑等效侧倾效应的二自由度整车运动模型[7]。该运动模型考虑了固定侧向加速度所引起的车身侧倾,其运动学方程如下:

(4)

(5)
式中:ms为簧载质量;hs为质心到侧倾轴线的距离;Kφ为悬架侧倾角刚度;g为重力加速度。
将式(5)代入式(4)整理得
(6)
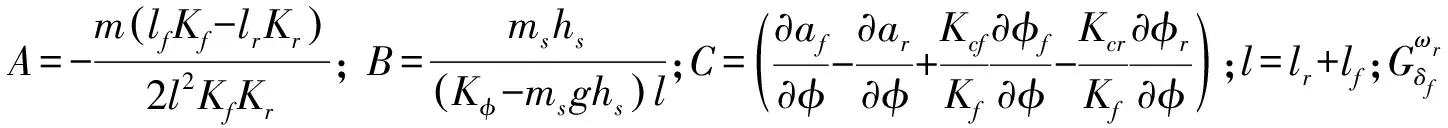
由式(6)得
(7)

由式(7)得
(8)
1.3 直流电机模型
本文选取直流电机为转角电机,根据直流电机的电枢电压平衡(忽略电枢电流变化所引起的电抗压降)、电磁转矩、输入输出转矩平衡建立电机的数学模型[8]。
电枢电压平衡方程为
u=Ri+keω
(9)
式中:u为电枢电压;R为电枢电阻;i为电枢电流;ke为反电势常数;ω为电机转子角速度。
输入输出转矩平衡方程为
(10)
式中:Te为电磁转矩;kT为电磁转矩常数;TL为负载转矩;B为阻尼系数;J为电机输出轴转动惯量;Tr为各种扰动转矩的总和。
整理(9)(10)可得电机运动状态模型:
(11)
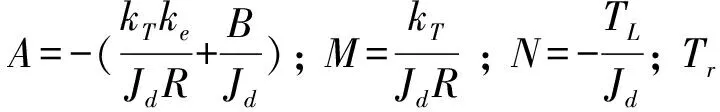
2 系统设计
2.1 变传动比曲线设计
对普通驾驶员来说,期望的转向系统增益在0.12~0.37 s-1之间最为适合,而对熟练的驾驶员来说,则在0.21~0.41 s-1之间比较合适[2,9]。因此,本文采用0.31 s-1的固定稳态转向系统增益来设计车辆的变传动比曲线,如图2所示。

图2 固定稳态转向系统增益的变传动比曲线
由图2可知:固定稳态车辆系统的变传动比曲线从0开始逐渐变化,并且在车速大于140 km/h时有明显下滑的趋势,但这并不满足AFS低速灵敏、高速稳定的要求。需要在此曲线的基础上进行改进。传统变传动比曲线会造成转角电机角加速度突变,冲击齿轮机构,影响其使用寿命。当车辆行驶在30 km/h以上时,车速对车辆操纵稳定性的影响较大,随着车速的提高,车辆的操纵稳定性逐渐降低[10]。因此,本文提出用反正切函数对中速段(35~100 km/h)的固定稳态转向系统增益的变传动比曲线进行拟合,改善车辆在中速段的稳定性。
本文选取v1=35 km/h,v2=100 km/h为上下临界车速,构造反正切函数:
2[is(v2)-is(v1)]arctan(ax+b)+
(12)
采用最小二乘法优化函数参数a、b,使得两者在中速段达到最佳逼近。求解a、b,得到拟合变传动比曲线,如图3所示。

图3 反正切函数拟合曲线
分析图3可知:相对于传统变传动比曲线,拟合变传动比曲线在低速传动比较小,高速传动比较大,明显提高了AFS低速灵敏、高速稳定的性能。
分析图4可知:拟合变传动比曲线在中速段的稳态转向系统增益波动较小,拟合效果较好,有利于提高车辆的操纵稳定性。

图4 拟合变传动比曲线转向系统增益
根据本文所选用的车辆参数(见表1),由式(3)得
(13)
则转角电机角位移与方向盘角位移的关系如图5所示。

图5 转角电机角位移曲面

参数名称数值质心到前轴的距离/m1.175质心到后轴的距离/m1.425前轴侧偏刚度/(N·rad-1)535 00后轴侧偏刚度/(N·rad-1)535 00整车质量/ kg 1 490簧载质量/kg1 177质心到侧倾轴线的距离/m0.28重力加速度/(m·s-2)9.8前轮外倾刚度/(N·rad-1)5 000后轮外倾刚度/(N·rad-1)5 000侧倾角刚度/(N·m·rad-1) 73 000前轮侧倾转向系数-0.055后轮侧倾转向系数0.118前轮侧倾外倾系数0.36后轮侧倾外倾系数0.28
2.2 全局快速Terminal滑模设计
相对于普通滑模控制,全局快速Terminal滑模控制能使系统状态跟踪误差在有限时间内收敛为0,系统的动态性能优异。此外,全局快速Terminal滑模控制无切换项,可避免系统抖振。因此,本文采用全局快速Terminal滑模快速、准确地跟踪本文设计的转角电机位置信号。
步骤1
设计全局快速Terminal滑动模态[11]:
(14)
式中:xd为给定位置指令;s0为位置跟踪误差;a0,β0>0;p0与q0为正奇数,并且p0>q0。
由式(14)知,当系统处于平衡状态(s1=0)时,
(15)
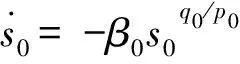
步骤2
由式(11)设计全局快速Terminal滑模鲁棒性控制律:
(16)

步骤3
(17)
整理式(11)(14)(16)得:
(18)
(19)
则


通过调整参数p、q、γ可使滑模面s1=0的领域Δ足够小。
步骤4
进行系统到达时间分析。整理式(19)(16)可得
(20)

习近平总书记在2015年提出了共建 “丝绸之路经济带”和“21世纪海上丝绸之路”的重大倡议,“经济带”和“丝绸路”被合并称为“一带一路”。“一带一路”倡议是一条促进中国与其他沿线国家之间共同发展、共同实现繁荣经济的合作共赢新思路。这一新兴倡议在经济带上的大力推进,有利于更加稳固地将中国的对外开放纳入新的历程。中国的企业必将会因此走出国门而涉及更多国家全球化投资活动,由此可见,在该倡议下,国际税收将迎来新的挑战,中国税收工作的国际化水平将会显著提高。
通过求解微分方程可得在滑动模态上从系统初始状态(s1≠0)到平衡状态的收敛时间为
由于γ1>η,则

综上可知,通过合理配置控制器参数a0、β0、p0、q0、φ、p、q、η、L可以使系统快速到达平衡状态,保证系统的控制精度、稳定性以及鲁棒性。
3 仿真结果分析
为了验证拟合后变传动比曲线以及全局终端滑模控制器的性能,在 Matlab/Simulink中建立电机模型、全局快速Terminal滑模控制器模型以及对比控制算法模型进行仿真实验,实验对比组采用比例积分微分(proportion integration differention,PID)算法,其控制器参数为:P=20,I=5,D=1。电机仿真实验参数如表2所示,全局快速Terminal滑模控制器仿真实验参数如表3所示。

表2 直流电机参数

表3 滑模控制器参数
3.1 拟合变传动比曲线及电机性能分析
固定方向盘转角为45°,车辆以3m·s-2的加速度,匀加速到120 km/h,对转角电机加入-35~35 N·m的随机扰动转矩负载,在这段时间内采用传统变传动比的转角电机角加速度,如图6(a)所示。采用拟合变传动比曲线的转角电机角位移和角加速度如图6(b)所示。分析图6(a)可知:传统变传动比曲线在分段点处(v1=35 km/h,v2=100 km/h),转角电机角加速度突变较大,会引起对变传动比齿轮机构的冲击,缩短其使用寿命。由图6 (b)可知:在车辆启动的瞬间,转角电机角加速度有轻微的突变;在余下的时间内,角加速度曲线光滑平缓。因此,拟合变传动比曲线明显改善了转角电机的角加速度波动。由图6 (c)可知:当v≤35 km/h时,转角电机与方向盘转向相同,使得在被动转向传动比的基础上减小了传动比;当v>35 km/h时,转角电机与方向盘转向方向相反,使得在被动转向传动比的基础上增大了传动比。这表明拟合传动比曲线是合理、有效的,满足了AFS的要求。

图6 车辆匀加速的电机位置信号跟踪
3.2 全局快速Terminal滑模性能分析
由图6(c)、(d)可知: PID算法超调量较大,系统进入稳态后,角位移误差在-0.02 ~0.02 rad之间波动。本文算法无超调,系统响应时间为0.01 s,进入稳态后角位移误差为0.08 rad。
固定车速为30 km/h,方向盘输入幅值为45°的正弦信号,对转角电机加入-35~35 N·m的随机扰动转矩负载,相应的转角电机角位移和角位移误差如图7所示。由图7可知:PID算法存在0.002 s的相位滞后,系统进入稳态后,角位移误差在-0.028~0.032 rad范围内波动。本文算法无相位滞后,系统进入稳态后,角位移误差维持在0.002 rad。
固定车速为30 km/h,给定方向盘45°的阶跃信号,对转角电机加入-35~35 N·m的随机扰动转矩负载,相应的转角电机角位移和角位移误差如图8所示。分析图8可知:PID算法超调43.5%,系统稳定后,角位移误差在0附近。本文算法无超调量,响应时间为0.07 s,系统进入稳态后角位移误差在0附近。

图7 固定车速方向盘正弦输入的转角电机位置信号跟踪

图8 方向盘正弦输入的电机位置信号跟踪
通过以上分析可知:本文算法响应速度快、无超调,系统稳定后跟踪误差小。在加入随机扰动后,算法具有较强的鲁棒性,并且适用于车辆行驶的各种工况。该算法能应用于AFS的转角电机角位移控制。
4 结束语
本文采用函数参数化的思路,提出用反正切函数对基于固定转向系统稳态增益的变传动比曲线进行局部拟合,得出拟合变传动比曲线。采用全局快速Terminal滑模算法,设计了滑模鲁棒控制律。分析结果表明:该方法拟合的变传动比曲线不仅满足AFS的性能要求,还明显减弱了转角电机的角加速度波动。本文算法响应快、无超调量,能够快速、准确地跟踪本文所设计的转角电机角位移信号。该算法能应用于AFS的转角电机角位移控制。
[1] ZHANG J,KIM J,XUAN D,et al.Design of Active Front Steering (AFS) System with QFT Control[J].International Journal of Automotive Technology,2008,9(6):695-702.
[2] TAJIMA J,YUHARA N,SANO S,et al.Effects of Stee-ring System Characteristics on Control Performance from the Viewpoint of Steer-by-Wire System Design[C]//International Congress & Exposition.1999.
[3] 石万凯,罗才伟,李伟,等.EPS+AFS集成转向系统分析[J].机械设计,2017(2):1-6.
[4] 欧阳伟.集成AFS和EPS的转向控制系统研究[D].长沙:湖南大学,2013.
[5] 王俊.基于变角传动比的汽车线控主动转向控制策略研究[D].合肥: 合肥工业大学,2017.
[6] 周兵,范璐,骆晨.主动前轮转向变传动比曲线分析与设计[J].湖南大学学报(自然科学版),2014,41(2):73-78.
[7] ABE M.Vehicle Handling Dynamics-Theory and Application[M].London:Butterworth-Heinemann,Elsevier Ltd,2009:80-95.
[8] 奚文龙,唐文秀,许李尚,等.基于一阶低通滤波器滑模反步法的直流电机位置控制[J].重庆邮电大学学报(自然科学版),2017,29(4):550-556.
[9] WEIR D H,DIMARCO R J.Correlation and Evaluation of Driver/Vehicle Directional Handling Data[C]//Automotive Engineering Congress and Exposition.1978.
[10] 郭孔辉,轧浩,宗昌富.横摆角速度反馈汽车转向控制的理论研究[J].中国机械工程,2000,11(2):70-73.
[11] YU S,YU X,MAN Z.Robust global terminal sliding mode control of SISO nonlinear uncertain systems[C]// Decision and Control,2000.Proceedings of the,IEEE Conference on.USA:IEEE,2000:2198-2203.

