一类SEIR流行病模型的全局稳定性分析

赵亚飞，苏 强，吕贵臣

(重庆理工大学 理学院， 重庆 400054)

全局稳定性问题是传染病动力学研究中的重要课题。对于传染病动力学模型全局稳定性的研究主要有2种方法：一是Lyapunov-LaSalle稳定性定理[1]; 二是Li-Muldowney几何方法[2-4]。Lyapunov-LaSalle稳定性定理主要是通过构造Lyapunov函数,利用Poincaré-Bendixson定理、Lyapunov-LaSalle稳定性定理等来研究平衡点的稳定性。郭丽娜等[5]通过构造Lyapunov函数，利用LaSalle不变性原理研究了平衡点的全局稳定性。陈永雪[6]通过构造Lyapunov函数，利用Poincaré-Bendixson定理、Lyapunov稳定性定理的LaSalle不变性原理研究了模型的全局动力学行为。马明菊等[7]利用Hurwitz判据判断了平衡点的局部稳定性，然后通过构造Lyapunov函数，利用LaSalle不变性原理研究了平衡点的全局稳定性。郭树敏等[8]通过构造Lyapunov函数，利用Lyapunov稳定性定理LaSalle的不变性原理研究了无病平衡点的全局稳定性，并构造Dulac函数，利用Poincaré-Bendixson定理验证系统是否存在周期解，从而研究全系统的稳定性等。其他相关文献见文献[9-12]。

构造Lyapunov函数往往比较困难。因此，Li-Muldowney基于高维Bendixson判据提出了全局稳定性判定的几何方法。利用该方法，Iwami等[13-14]研究了一类禽-人SI-SIR流行病模型的全局稳定性；苟清明等[15]研究了带有垂直传染和接种疫苗SEIRS流行病模型的全局稳定性；Chen等[16]考虑了H7N9病毒在人类中发生突变的禽流感模型的全局稳定性。此外，Lu等[17]利用Li-Muldowney几何方法研究了一类三维Lotka-Volterra系统的全局稳定性；Lu等[18]分析了一类具有Gompertz增长的三维竞争模型的全局稳定性；文献[19]借助于时间平均性质，在Li-Muldowney基础上，提出了全局稳定性判定的新方法。

本文主要考虑如下具有常数移民的SEIR流行病模型：

(1)

其中：S(t)、E(t)、I(t)、R(t)分别表示易感染者、潜伏者、受感染者和移除者在t时刻的数量；N(t)表示t时刻的总数量，记N(t)=S(t)+E(t)+I(t)+R(t)；μ表示自然死亡率；γ0表示潜伏者和受感染者之间的转移率；常数k0表示移除率；β10、β20、β30分别表示潜伏者、受感染者和移除者的有效接触率；(1-p)A和pA分别表示易感染者和潜伏者的常数输入。

(2)

若令x=1-Y-Z-R1,y=Y,z=Z,则可得系统 (2)的极限系统为：

(3)

其中β2>β3。

李桂花等[20]通过对模型(3)的全局稳定性的详尽的分析得到：

定理1 如果R0>1,β1>β3且cβ1(1-p)<1-γ，cβ3(1-p)<1+p，则系统(3)唯一的地方病平衡点E*是全局渐近稳定的。

1 预备知识

考虑微分方程

(4)

其中B=PfP-1+PJ[2]P-1，矩阵Pf为

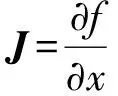
此外，吕贵臣等[18]基于时间平均性质，对定理1做了推广，得到了如下结论：

其中

2 全局稳定性分析

本节将借助已提出的全局稳定性方法改进已有的结果。应用定理3得到如下结果：

定理4 如果R0>1,β1>β3且cβ1(1-p)<1,则系统(3)唯一的地方病平衡点E*是全局渐近稳定的。

证明简单计算得系统(3)的雅可比矩阵J为

其中：

j11=-1+cβ3x-c[β1y+β2z+β3(1-x-y-z)]

j22=-cβ3x+c[β1y+β2z+β3(1-x-y-z)]

可得其2阶可加性复合矩阵J[2]为

其中：

J11=c(β1-β3)x-γ-2+cβ3x-

c[β1y+β2z+β3(1-x-y-z)]

J22=-2+cβ3x-c[β1y+β2z+

β3(1-x-y-z)]-k

J32=-cβ3x+c[β1y+β2z+β3(1-x-y-z)]

J33=c(β1-β3)x-γ-2-k

其中：

c[β1y+β2z+β3(1-x-y-z)]

c[β1y+β2z+β3(1-x-y-z)]

又由系统(3)可得：

x<1-p

则有：

β3(1-x-y-z)]+cβ1x<

β3(1-x-y-z)]+cβ1(1-p)<

此时：

由定理3可得,系统(3)是全局渐近稳定的。

3 结束语

本文主要考虑了具有常数移民的SEIR流行病模型。研究的主要目的在于弱化地方病平衡点全局稳定性的条件。利用全局稳定性判别的新方法改进了文献[20]中关于地方病平衡点全局稳定的结果。

[1] LASALLE J P.The stability of dynamical systems[J].1976,27(11):1121-1130.

[2] LI M Y,MULDOWNEY J S.Global stability for the SEIR model in epidemiology[J].Mathematical Biosciences,1995,125(2):155-164.

[3] LI M Y,MULDOWNEY J S.A geometric approach to global-stability problems[J].SIAM Journal on Mathematical Analysis,1996,27(4):1070-1083.

[4] LI M Y,WANG L.Global Stability in Some Seir Epidemic Models[J].Institute for Mathematics and Its Applications,2002,126：332-336.

[5] 郭树敏,郭丽娜,李学志.具有饱和治疗的禽流感动力学模型的研究[J].数学的实践与认识,2010,40(3):134-137.

[6] 陈永雪.基于禽中低致病性的H7N9禽流感模型的动力学性质[J].生物数学学报,2014(4):627-634.

[7] 马明菊,李君.一类具有潜伏效应的H7N9模型的动力学性质[J].莆田学院学报,2016,23(5):4-8.

[8] 郭树敏,李学志.具有常数输入的H7N9 禽流感动力学模型分析[J].信阳师范学院学报(自然科学版),2017,30(1):13-16.

[9] JIANG Y,CHEN Y.Dynamic Analysis of an Infectious Disease between Human and Poultry[J].Journal of Biomathematics,2013,4:003.

[10] 郭树敏,姚峰,李学志.一类具有治疗的禽流感模型分析[J].数学的实践与认识,2015,45(1):192-196.

[11] 殷其琴,冯光庭,张兴安.两类禽流感模型的动力学分析[J].应用数学,2015,28(3):481-489.

[12] 陈瑶,孙法国,胡新利,等.带有媒体报道的H7N9传染病模型的研究[J].Advances in Applied Mathematics,2015(4):285-291.

[13] IWAMI S,TAKEUCHI Y,LIU X.Avian-human influenza epidemic model[J].Mathematical Biosciences,2007,207(1):1-25.

[14] EUNOK J,IWAMI S,TAKEUCHI Y,et al.Optimal control strategy for prevention of avian influenza pandemic[J].Journal of Theoretical Biology,2009,260(2):220-229.

[15] 苟清明,刘春花.带有垂直传播和接种疫苗的SEIRS传染病模型的全局稳定性[J].西南大学学报(自然科学版),2010,32(11):55-61.

[16] CHEN Y,WEN Y.Global dynamic analysis of a H7N9 avian-human influenza model in an outbreak region[J].Journal of Theoretical Biology,2015,367:180-8.

[17] LU G,LU Z.Geometric approach for global asymptotic stability of three-dimensional Lotka-Volterra systems[J].Journal of Mathematical Analysis and Applications,2012,389(1):591-596.

[18] LU G,LU Z.Geometric approach for global asymptotic stability for three species competitive Gompertz models[J].Journal of Mathematical Analysis and Applications,2016,445(1):13-22.

[19] LU G,LU Z.Geometric approach to global asymptotic stability for the SEIRS models in epidemiology[J].Nonlinear Analysis:Real World Applications,2017,36:20-43.

[20] LI G,WANG W,JIN Z.Global stability of an SEIR epidemic model with constant immigration[J].Chaos Solitons and Fractals,2006,30(4):1012-1019.