基于不同损伤评价标准的正面碰撞乘员保护研究

胡远志，甘 顺，刘 西，蒋成约，任立海

(汽车零部件先进制造技术教育部重点实验室， 重庆 400054)

近年来，随着生物损伤力学相关方向的研究不断深入，在汽车乘员保护领域，基于大量尸体试验和交通事故调查后得出的乘员损伤准则为研究分析乘员在汽车碰撞事故中的受伤程度提供了指导。研究人员针对头部、胸部、颈部、腹部、腿部等部位分别提出了多种损伤准则和相应的伤害限值。国内外的相关道路交通安全管理机构也相继颁布了相应的法规和行业标准。如国外最新版本的FMVSS208[1]和ECE R94[2]法规提出加权综合损伤指标WIC(weighted injury criteria， WIC)。国内第1版 C-NCAP(China-new car assessment program)于2006年开始实施之后，为促进汽车安全技术的发展，相继提出2012版[3]、2015版[4]、2018版[5]3版管理手册。在不同的标准中，身体各部位可能会考察不同的损伤准则，并对各个伤害准则分配不同的权重。考察标准的不同会直接导致整个约束系统在开发过程中匹配策略的改变，从而影响量产车型的安全性能。

本文利用Polynomial SVD、Kriging、神经网络3种算法分别建立代理模型，在验证模型的拟合精度后选取精度最高的神经网络算法进行优化，并通过边界样本点检验后发现代理模型的局限性。最终运用多刚体MADYMO模型分别以多目标优化、加权综合评价指标WIC、C-NCAP评分3种评价指标，通过MOGA-Ⅱ遗传算法进行优化。结果表明：多目标优化收敛速度慢导致计算成本高，且高维空间不具有直接可观测性，因此多目标优化并不适用于工程优化;以WIC和NCAP为优化目标的单目标优化能快速得到最优解，且表现出不同的侧重点,这与2个指标在不同部位分配的权重和阈值不同有关。

1 正面碰撞驾驶员侧伤害值分析

由于前排乘员较驾驶员拥有更加充足的车内空间，所以在正面碰撞过程中，驾驶员往往容易受到更加严重的伤害，如C-NCAP针对前排假人评分就是以驾驶员侧假人伤害值为基准，只有当乘员侧假人某部位的得分低于驾驶员侧相应部位得分时，才采用乘员侧相应部位得分来替换[3-5]。因此，本文仅以驾驶员侧的约束系统匹配为例进行优化分析。

1.1 驾驶员侧约束系统模型

本文采用本课题组已经完成工程对标分析并通过多工况验证了模型可靠性的某款中型SUV驾驶员侧MADYMO约束系统模型作为基础模型进行分析[6]，如图1所示。

1.2 人体各部位常用损伤标准

生物损伤力学是生物力学领域中专门研究由生物与力的相互作用产生损伤的相关学科。近年来，随着损伤流行病学的发展和各类事故数据库的建立，以统计学的科学方法分析相关结果得到的能评价事故载荷严重性和损伤风险的损伤标准逐步得到广泛应用。现阶段各部位普遍使用的评价标准如表1所示。

图1 驾驶员侧约束系统模型

部位损伤标准注解头部HIC36、HIC15头部损伤准则H3ms头部加速度3 ms准则颈部Nij颈部轴向力和弯曲力矩的线性合成准则FX、FZ颈部剪切力、轴向伸展力MY颈部绕Y轴弯曲胸部C3ms胸部加速度3 ms准则Cdef胸部压缩变形量VC胸部粘性准则大腿Ff股骨压缩力Knee Slide膝盖滑动位移小腿TI胫骨指数Tf小腿压缩力

1.3 不同归一化损伤评价标准

1.3.1 不同WIC标准

国内外相关研究人员参考实际交通碰撞事故的统计数据，用身体不同部位在事故中发生损伤的统计概率作为综合损伤指标中各项损伤值的权重，得到不同标准下的加权综合损伤指标WIC。

如依据大量成人尸体试验得到的FMVSS208法规中规定的损伤标准为

(1)

参考David等和张维刚等[7]的研究成果，并根据最新版本的FMVSS208和ECER94法规，白中浩等[8]提出了适合高维目标优化问题的损伤标准：

(2)

清华大学王琮[9]基于Viano 等提出的综合评价方法得到适应MADYMO多刚体假人模型的损伤输出权重分布：

(3)

其中Ffr、Ffl为左右大腿轴向力峰值。HIC36_T、C3ms_T、Cdef_T、Ffr_T和Ffl_T各伤害值的限值如表2所示。

表2 各损伤指标限值

3种指标虽然具体的权重值略有差别，但主要都侧重考察头部和胸部伤害。相比前两种WIC准则，王琮的评价指标中囊括了颈部损伤，能更加全面地评价假人伤害，所以本文以此作为WIC优化目标准则。

1.3.2 2018版C-NCAP正面碰撞评分标准

由于NCAP较WIC评分规则更加复杂，考察的损伤准则和阈值也有较大差别，表3罗列了2018版C-NCAP关于100%重叠刚性壁障碰撞试验中针对驾驶员所考察的伤害指标阈值区间，便于以下的比较说明。

表3 2018版C-NCAP主驾伤害阈值

2 约束系统模型的优化设计

2.1 代理模型建立

为减少计算量，节约计算成本，研究人员运用Polynomial SVD[10]、Kriging[11]、神经网络[12]等算法训练一定数量样本，然后建立代理模型，并对原有模型进行替换。首先，运用试验设计的方法并依据约束系统零部件供应商提供的参数范围，确定输入参数的取值空间，从中筛选出一定数量的设计点，对其进行求解计算。约束系统的匹配空间如表4所示。然后根据样本空间建立代理模型。最后依靠代理模型进行优化分析，并进行模型验证[13]。

表4 约束系统的匹配空间

由式(4)可以计算得到训练多项式代理模型的最小样本数量。本模型具有6个输入变量，训练1个3次多项式响应面模型最少需要84个样本点。同时，应遵循至少2倍最小样本数训练代理模型的基本原则。因此，本文采用超均方分布[14]，在整个设计空间中选取了200个设计点进行仿真计算。并基于样本空间分别以Polynomial SVD、Kriging、神经网络3种方法建立代理模型。不同方法得到的代理模型的拟合情况如表5所示。结果表明：根据已有的样本数量已经能拟合得到拟合精度很高的代理模型。

(4)

其中：M为代理模型的输入变量个数；N为多项式响应面的次数；DOEP为训练多项式响应面代理模型需要的最小样本数量。

表5 代理模型拟合情况

随机生成10个样本对代理模型进行模型精度验证。在理想状态下，代理模型能表征原有模型，即原模型的仿真计算结果应该与代理模型的预测值一致。如图2所示，代理模型得到头部伤害值指标HIC值越靠近斜率为1的参考线，说明预测效果越好。通过比较可以看出：基于神经网络算法预测得到的HIC值与参考线距离最近，并将之前的200个样本点一同分析，发现神经网络模型的R2值最接近1(见表6)，说明该代理模型预测能力最强。故选取应用神经网络算法建立的代理模型作为后续优化的基础模型。

图2 基于不同算法的响应面模型预测结果

代理模型R2值神经网络算法0.999Kriging法0.998三次响应面法0.982

2.2 代理模型多目标优化

依据本文建立的神经网络代理模型，运用MOGA-Ⅱ进行100代的优化，共得到1 814组数据。从这些设计空间中选取Pareto非劣解集，并选取重要的头部HIC和胸部变形量构建如图3所示的散点图。选取其中5个边沿点进行MADYMO多刚体求解计算，以此验证代理模型的可靠性。

图3 代理模型Pareto解集

求解原模型得到各部位伤害值，并与代理模型预测的相应伤害值进行比较，计算两者的平均误差值，结果如表7所示。

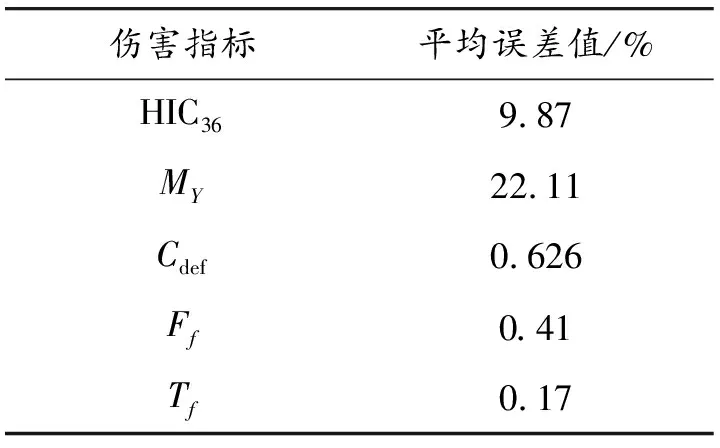
表7 代理模型预测误差

通过比较发现:虽然神经网络训练出来的代理模型在一定误差范围内能预测原有仿真模型,但可以观察到，需要将大量的样本进行训练后才能得到具有一定精度的模型。由于存在边界接触的现象，如果样本空间中未完全涵盖此类设计点，预测点就可能在该处与原模型存在较大误差。比如本算例中一组试验由于气囊刚度过低，假人头部与方向盘发生二次接触，导致预测模型与仿真模型头部和颈部伤害值存在35%以上的误差。因此，为避免工程中此类问题带来的风险，本文并未采用代理模型代替原有模型进行计算。

2.3 原模型多目标优化

理想的约束系统优化是得到一组最佳的匹配参数，使得每个部位的伤害指标在该系统下都能达到最低值，从而最大限度地发挥其保护乘员的作用。但多目标优化由于各参数之间存在较高的相关性，往往难以得到全局的绝对最优解，只能根据各输出参数得到非劣解集，但高维的多目标优化问题可观察性较差。本文根据该车型进行多伤害标准值(见表1)最低的多目标优化仿真分析，期望得到高度集中的Pareto非劣解集。

本模型运用MOGA-Ⅱ算法进行60代共1 280组的仿真计算。为了更好地观察不同约束系统匹配参数和输出伤害值的变化历程，分别做如图4～6所示的优化历程图。首先，为方便不同约束系统匹配参数间的比较，将不同的数据进行了0-1标准化处理。每个圆点表示一组试验对应的约束系统匹配参数值或乘员不同部位的伤害值，颜色的变化表示优化历程。然后，随着优化的进行，新的试验组对应的圆点依次按照从右到左排序。从图4～6中可以观察到：试验组在某个区间内重复率越高，相应的试验点分布越宽，即表示在该处的概率密度越大。

图4 约束系统参数优化分布历程

由图4可见：在多目标优化过程中，除安全带限力值和预紧触发时刻随着优化的进行逐渐集中在一个较小的区间内，其余参数并未收敛于一个稳定的区间中，因此导致即使优化完成后也很难选取合适的约束系统匹配参数值。

图6 胸部和下肢损伤值分布历程

同样，通过观察图5和图6可以发现：在基于此方法的多目标优化过程中，多数部位的伤害值并未集中于一个较窄的区间内，说明多目标无法同时达到最优值。但从总体趋势可以看出：随着优化的进行，所有损伤值都逐渐向低水平集中，需注意其中FX和Cdef计算输出量为负值。

比较不同部位的优化历程图可以看出:胸部的伤害值收敛于一个相对集中的区间内。由于经过遗传算法优化后的样本数据已经朝着优化空间集中，影响了统计样本的分布,故以之前的200组超均方分布样本为分析样本，分析各约束系统参数输入量对胸部压缩量和黏性准则的效应量，发现安全带限力等级对2个伤害值均有很高的效应量值且远高于其他输入参数的影响。同时，结合图4中安全带参数表现出的与胸部伤害值一致的收敛趋势也能说明两者具有高度相关性。

图7 各输入参数对胸部伤害值的效应量

单独观察头部伤害值HIC36和H3ms，2个伤害值直到收敛结束时仍在很大一片区间内浮动(见图5)。而多目标的优化过程需要考察整个多维输出是否收敛于1个多维的空间区间内，但考虑到高维空间的可视化效果较差，因此本文选取了头部HIC36和胸部Cdef两个分配权重相对较高的损伤标准做如图8所示的二维图，观察是否存在具有代表性的Pareto非劣解集。由图8可以看出：随着优化的进行，大约在1 100代以后，多数设计点开始集中在一个相对较小的区域内，即HIC36和Cdef的Pareto解集。

图8 多目标优化头部与胸部Pareto解集

虽然图8说明了优化算法的有效性，但也反映出基于多目标伤害值最低的优化需要经过大量、多代的遗传优化才能得到Pareto解集，且高维Pareto解集难以直接得到最合适的约束系统匹配参数。

2.4 WIC优化

通过WIC优化历程(图6)可以观察到：优化模型在计算到300组时，输出的WIC值基本已经达到极小值。之后，经过500组的交叉和变异遗传后，WIC依然收敛于0.48附近，说明该优化模型已经达到全局最优解。

图9 WIC优化历程

按照WIC分数升序排列，得到分数最低的设计点，其ID号为785。提取该方案的输入参数，结果如表8所示。表9列出了各项伤害值的具体数值。

表8 WIC最优解匹配参数

表9 WIC最优解损伤情况

基于WIC的评价指标，着重考察乘员在关键部位的损伤情况并降低其伤害值，有利于在恶劣工况下更好地保护乘员头部和胸部，降低发生严重伤亡的风险。

2.5 C-NCAP优化

观察C-NCAP优化历程的总分变化(图10)可见：与基于WIC的优化结果相似，优化模型在计算到300组时已经能得到比较稳定的极大值，且经过遗传算法的500组的变异和交叉运算后依然收敛于13.6分，说明已经得到全局最优解。

图10 C-NCAP优化历程总分变化

按照C-NCAP总分的降序排列，得到分数最高的设计点，其ID为486。提取该方案的输入参数，结果如表10所示。表11列出了部分伤害值的具体数值。

表10 C-NCAP最优匹配参数

表11 C-NCAP最高分伤害情况

由于在工程开发中对车辆的设计更多体现的是一种应试要求，因此基于C-NCAP的约束系统具有直接高效、工程指导性强、考察伤害值全面的特点。

3 不同评价标准的比较分析

3.1 多目标优化与归一化目标优化比较

无论是多目标还是单目标优化的目的都是通过有限的优化历程得到一组可靠的约束系统匹配参数，用于指导工程实践。因此，分别做安全气囊点火时刻和泄气孔直径缩放系数箱型图(图11和图12)。由图11、12可以看出：在基于NCAP和WIC的单目标优化历程中，气囊参数集中在一个很小的区间中，便于工程中匹配参数的确定；相反，多目标优化的参数值则分布在很广的区间中，且没有相对集中的参数值。因此，在工程中多目标优化的方法并不具有实用性。

图11 安全气囊点火时刻比较

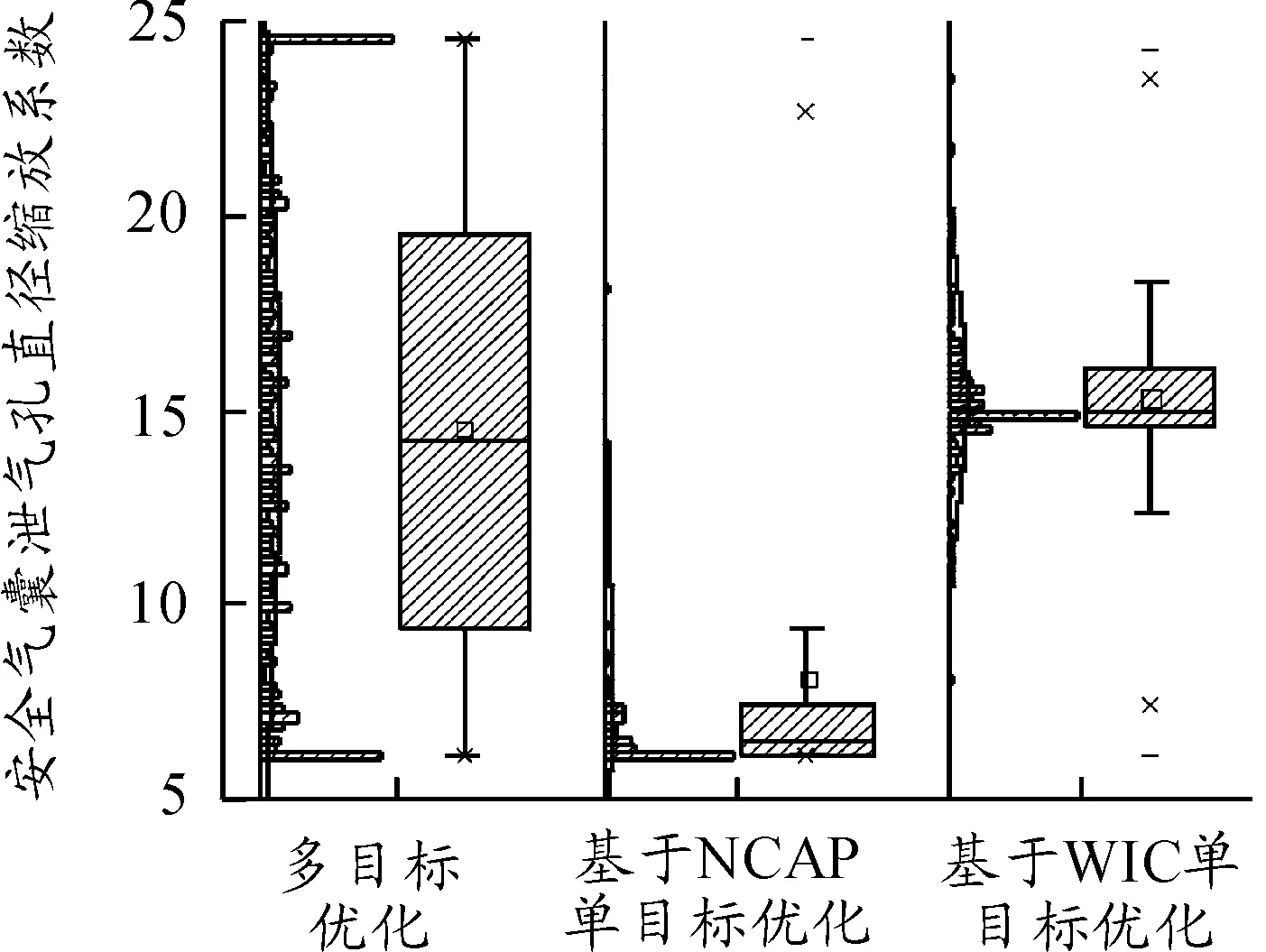
图12 安全气囊泄气孔直径缩放系数比较

3.2 C-NCAP与WIC评价比较分析

3.2.1 优化结果对比

WIC的评分遵循伤害值越低得分越高的原则，而C-NCAP则是满足低于一定阈值要求后便可得满分，而且两者在各部位伤害值分配的权重不同(见表12)。由于2种标准侧重点和评价方法的各异，导致最终优化得到的伤害值也存在一定差异。2种方案在2种标准下得到的分值如表13所示，可见两者主要的差别存在于头部和胸部。

表12 两种评价指标各部位损伤权重

表13 两种标准最优解得分对比

同时，比较基于WIC和C-NCAP优化得到的两套约束系统方案，主要存在如表14所示的匹配参数的差异。因此，接下来分析导致两者在相关参数上存在差别的原因。

表14 两种标准匹配参数差异比较

3.2.2 安全带及气囊匹配差异分析

从表13中的18版C-NCAP评分可知：此车型的前排驾驶员在两套方案中胸部均为主要失分点，此外小腿有0.1左右的失分，其他部位均为满分。同时，两套方案以WIC为评分标准得出的分值主要区别在头部，颈部和胸部分值变化相对并不明显。WIC中头部分配了超过一半的权重，C-NCAP中胸部和头部则占有相同的权重值(见表12)。

由表13中还能看出：基于WIC优化得出的头部伤害值比基于C-NCAP优化得到的伤害值要低，但同时胸部伤害值却更高。故可通过分析随机样本空间计算头部HIC36和H3ms对胸部Cdef和VC的效应量，研究两者之间的相关性，结果如图13所示，其中：胸部HIC36(p<0.001)和H3ms(p=0.001)对Cdef均有显著影响；胸部HIC36(p<0.001)和H3ms(p=0.008)对VC也有显著影响。

图13 头部与胸部伤害指标相关性

从图13可以发现：头部损伤值和胸部损伤值之间成相反作用关系(Cdef输出为负值)，即降低头部伤害值后会相应地导致胸部伤害值在一定程度上有所提高，此规律也与两套最优匹配方案的损伤值结果相符。因此，基于C-NCAP优化的关键问题就是权衡头部和胸部伤害值之间的关系。

做如图14所示的头部伤害值优化历程图，HIC36和头部3 ms合成加速度在200组以后很大部分值处于某水平趋近线上下，而此值恰为该伤害值阈值区间的下限(HIC36等于650，H3ms等于72g)，且随着优化的进行伤害值一直稳定于限值。说明以C-NCAP总分最高为优化目标，最优匹配方案必须是各项数值均衡最优，一味降低某个部位的损伤值对于提高总分并没有帮助。

图14 头部伤害指标优化历程

综上所述，此算例中针对的是2018版C-NCAP评分的优化策略：在保证头部不失分的前提下，尽量降低胸部伤害值，而安全带限力等级与胸部伤害最直接相关(见图7)，因此算法最终匹配到最低值2 kN。同时，为保证整个约束系统对假人的约束能力，需要提高气囊刚度，可通过降低泄气孔直径来弥补安全带刚度的不足。本算例中气囊泄气孔匹配直径也为取值区间的下限值20 mm。

针对WIC的优化策略是优先考虑保护头部，即在胸部伤害值的减少量乘以权重后对总分的影响量没超过头部的影响量时，优化过程总会以分配权重最高的头部为首要优化目标。

3.2.3 转向管柱匹配差异分析

为研究不同转向管柱溃缩力对乘员各部位伤害的影响，在WIC最优组的基础上，改变转向管柱溃缩力，保持其他匹配参数不变。由计算结果发现：对于匹配有安全气囊和佩带安全带的乘员约束系统而言，更高的转向管柱溃缩力能在管柱溃缩期间对乘员头部起到更好的支撑作用。如图15所示，增大转向管柱溃缩力，能增加头部加速度曲线的峰值脉宽，降低最大峰值，从而有效降低假人头部伤害值。但是更大的压溃又会增加胸部的伤害值(如图16所示)。WIC指标中头部的权重较胸部大，所以在整个优化过程中会首先考虑降低头部伤害值，最终匹配得到较高的转向管柱溃缩力(Column_force为4.64 kN)。相反，基于NCAP的优化结果，当头部已经达到满分要求后，会通过降低转向管柱溃缩力来降低胸部伤害值，从而得到更高的总评分。

图15 不同管柱溃缩力下，假人头部加速度

图16 不同管柱溃缩力假人头部加速度

4 结论

1) 在具有足够样本空间和一定误差允许范围内，运用试验设计的方法选取设计样本，基于各类算法建立代理模型，并依靠遗传算法优化得到Pareto解集的方法，确实能得到可靠的代理模型。但由于模型本身存在边界接触等容易导致边界突变的限制条件，预测模型可能在此类设计空间内与真实模型存在较大误差，所以在工程实践中并不建议直接采用代理模型进行优化得到匹配方案。

2) 以降低多个伤害值为目标的多目标优化由于收敛速度慢、可观测性差等原因并不适用于工程应用。相比之下，对身体各部位分配合适权重值的单目标优化能快速高效地得到直观的约束系统匹配参数。

3) 基于两种不同的归一化损伤评价标准，通过启发式算法智能优化计算得到了2组不同的约束系统匹配方案。可以发现，基于2组不同标准的优化过程采取了2种不同的优化策略。基于WIC的优化主要根据不同部位所占的总伤害值的比重大小，以权重作为优先级，首先考虑将重点部位的伤害值降到最低；基于2018版C-NCAP的优化则表现为一类更加均衡的匹配方式，当某个部位的伤害值已经达到高限后，将综合考虑其他部位的伤害情况，从而达到更高的总评分。

虽然在工程中，此类优化方法并不常见，且往往在约束系统参数匹配时还会预留一定的刚度余量，避免在实际碰撞中由于约束系统刚度不足导致假人与车体的二次碰撞，但本文的研究结果可以为今后开展自适应约束系统相关方向的研究提供参考。

本文的研究结果也引发了一个讨论：在实际工况中，是以NCAP中的类似木桶理论原理的方式来均衡降低乘员伤害，还是以WIC评价中以降低重点部位的伤害值为主要优化目标，还需要进一步通过生物损伤试验或者交通事故数据来验证。

[1] National Highway Traffic Safety Administration.Federal motor vehicle safety standards:Occupant crash protection[J].Federal Register,1997,62:812.

[2] ECE U N.Uniform Provisions Concerning the Approval of Vehicles with Regard to the Emission of Pollutants According to Engine Fuel Requirements[J].UN ECE Regulation,2005(83).

[3] C-NCAP管理中心.C-NCAP管理规则(2012版)[S].天津:中国汽车技术研究中心,2012.

[4] C-NCAP管理中心.C-NCAP管理规则(2015版)[S].天津:中国汽车技术研究中心,2015.

[5] C-NCAP管理中心.C-NCAP管理规则(2018版)[S].天津:中国汽车技术研究中心,2018.

[6] 胡远志,梁永福,刘西,等.基于坐标系转换的乘员约束系统精确建模[J].汽车工程,2016,38(5):574-579.

[7] 张维刚，何文，钟志华．车辆乘员碰撞安全保护技术[M]．长沙：湖南大学出版社，2007.

[8] 白中浩,卢静,王玉龙,等.基于降维的驾驶员侧约束系统高维目标优化[J].中国机械工程,2014,25(11):1556-1561.

[9] 王琮，针对多种碰撞工况的乘员约束系统构型设计方法研究[D].北京：清华大学,2010.

[10] SCHMIT L A,FARSHI B.Some Approximation Concepts for Structural Synthesis[J].AIAA Journal,1974,12(5):692-699.

[11] 张维刚,刘晖.Kriging模型与优化算法在汽车乘员约束系统仿真优化中的应用研究[J].湖南大学学报(自然科学版),2008,35(6):23-26.

[12] 王文成.神经网络及其在汽车工程中的应用[M].北京：北京理工大学出版社,1998.

[13] 高晖,李光耀,李铁柱.基于遗传算法和可靠性分析的乘员约束系统优化[J].汽车工程,2008,30(12):1052-1055.

[14] 陈浩.复杂结构拉丁超立方设计的结构[D].天津：南开大学，2013.

[15] DAVID C V，SUDHAKAR A．Assessing the Safety Performance of Occupant restraint Systems[C]//Procee-dings of the SAE World Congress．Detroit:SAE Technical Paper.1990:902328．.