“圆锥的体积”教学研究报告

一、问题

在人教版小学数学教材中，圆锥的体积被编排在六年级下册第三单元，紧接圆柱的认识这一知识内容。对这一内容，教材先提出“我们已经会计算圆柱的体积，如何计算圆锥的体积”这个问题，通过两个孩子的对话引导学生建立圆柱与圆锥的关系，并设计了“探究一下圆锥与圆柱体积之间的关系”的实验。实验的具体操作流程是：各组准备好等底等高的圆柱、圆锥形容器，用倒沙子或水的方法发现两者之间的体积关系，得出圆锥的体积公式。

诚然，教材这种“提出问题→建立关系→动手操作”的整体设计是非常系统、完整的。但是仔细思考后我们不难发现：教材对实验探究的开放性指导不够。要探求圆锥的体积，圆柱有着非常明显的先入为主的味道，两者体积关系的建立、实验器材的选用、实验的设计似乎都来源于教师（教材），缺少学生温故知新、甄别遴选的探索过程，到最后，学生不仅对圆锥体积的认识缺乏深度，在探究能力与创新能力的培养上，效果也是大打折扣。对于学生来说，无论是圆柱的被选中还是实验器具的优化，以及倒水倒沙的实验方法，都需要在对圆锥体积的探究过程中遇到问题而逐步产生。基于这一认识和对学生认知规律的尊重，我们工作室对这一内容的教学进行了研究，试图通过这一个课例研究“用操作获取结论”的这一类课例，尽可能多地发挥这类教材所承载的教育功能，以培养学生的理性精神。

（一）教学实践中的问题

（二）解决问题的策略

弗赖登塔尔说，“学习数学的唯一正确方法是实行‘再创造”，也就是说由学生本人把要学的东西自己去发现或创造出来，教师的任务是引导和帮助学生进行这种再创造的工作。那么，教师如何引导学生通过自身的体验对“如果当时的人们有幸具备了我们现在已掌握的知识，他们是怎样把那些知识创造出来的”这一问题作出回答呢？

1.设计具有挑战性的问题

好问题能将学生的思维聚焦在探究方法的思考上，使学生兴趣盎然地投入到学习活动中，以求在掌握基础知识的同时，思考能力、主动获取知识的能力以及探索合作精神等都得到较好的发展。在研究圆锥体积公式时，教师可以设计问题：“今天我们要研究圆锥的体积，按照我们以前研究图形面积和体积的方法，你觉得应该怎样研究圆锥的体积呢？”引发学生类比迁移。

2.设计具有挑战性的活动

教师通过问题激活学生关于转化的经验，采用“面对新问题→联想旧知识→寻找新旧知识之间的联系→用旧知识解决新问题”的解决策略，学生亲历“选择关系→猜想关系→验证关系→运用关系”的全过程，学会用联系的方法学习数学。

（1）选择关系。学生在已有的图形知识里搜索与圆锥有关的立体图形时，会很自然地联想到圆柱，“都有圆形底面”是产生联想的重要依据。这时，教师不要急于给出等底等高的一组圆锥和圆柱作为实验器具，可设计一组与圆锥只等底、或只等高、或等底又等高、或不等底又不等高的圆柱供学生选择。这个选择的过程既是思辨的过程，也是理性分析的过程，有利于培养学生的几何直观能力。

（2）猜想关系。猜想实际上是学生对圆柱和圆锥关系的进一步思考。这种猜想源于学生的几何直观与自身经验，有利于培养学生的空间想象能力。

二、实践

基于“寻找关系，找准联系”的学习理念，我们给学生提供了开放的问题情境，遵循学生学习的自然路径，引导学生寻找解决问题的方法，经历公式产生的过程。

教学过程：

师：（出示一个圆锥）今天这节课，我们将研究圆锥的体积。（板书课题）关于几何图形，我们研究过平面图形的面积以及立体图形如长方体、正方体和圆柱的体积，回顾一下我们的研究方法，你觉得我们可以怎样研究圆锥的体积呢？

生1：一般会转化成我们熟悉的图形。

师：有道理！之前我们学习的图形大多都是转化成熟悉的图形进行推导的，那你们大胆地猜想一下，研究圆锥的体积，可以转化成哪个立体图形呢？

生2：应该是圆柱。

師：为什么不转化成长方体或正方体呢？

生2：圆锥和圆柱长得更像，底面都是圆形。

师：（出示图片）这是我们要研究的圆锥，这些圆柱如果要你来挑，你会挑哪一个圆柱来研究呢？先独立思考，然后在小组内交流你的看法。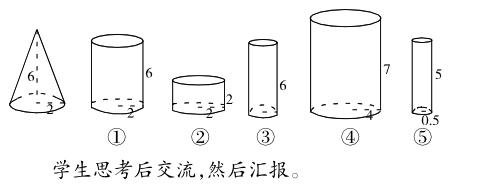

生3：我们觉得选①号圆柱比较靠谱，这两个图形的底面一样大。

生4：我们觉得选②号圆柱也有道理，底面一样大，高不同，说不定也有关系呢。

生5：我们觉得选③号圆柱也不错，圆柱的体积是底面积乘高，要么底相同，看高的变化与体积有没有关系；要么高相同，看底面积的变化与体积有没有关系。

生6：可是③号圆柱的底面没有数据，没办法研究啊。

师：真好！还知道用控制一个量不变的方法来研究。可惜，③号圆柱的底面半径没有提供。那为什么大家不选④号圆柱和⑤号圆柱呢？

生7：与要研究的圆锥相比，它们的底不一样，高也不一样，不太方便研究。

师：你们思考问题越来越有数学家的范了，了不起啊！那么，你们选择的圆柱与圆锥的体积可能存在怎样的关系呢？凭直觉猜猜看。

生8：圆锥的体积可能是①号圆柱体积的一半。

师：为什么？你能说说理由吗？

生8：我想把圆锥放到①号圆柱里面去，圆锥的底面应该恰好占满圆柱的底面，高与圆柱一样；如果把圆锥倒过来再放进去一次，结果是一样的，所以我猜想圆锥占圆柱体积的一半。

生9：老师，我有不同意见，我认为圆锥体积不是①号圆柱体积的一半，应该比一半小一些。

师：噢？你是怎么想的呢？

師：很遗憾，老师只找到了这样一套实验器材，（展示模型：等底等高的圆柱和圆锥）怎么办？

生14：先通过实验找出这两个物体之间的体积关系。

师：说说实验设想。

生14：既然是算体积之间的关系，我们可以用盛水的方法测量出这两个物体的容积关系。

生15：用圆柱形容器装满水，然后往圆锥形容器里倒，看看能倒满几次。

师：分组实验试试看。（生动手操作）

生16：真的能倒满3次，说明圆柱的体积是等底等高圆锥体积的3倍。

师：有没有人先把圆锥装满水往圆柱里倒的呀？

生17：肯定要倒3次才能装满圆柱。

师：如果只倒1次呢？

生动手操作，发现如果只倒1次，这时形成的圆柱其实就是刚才的②号圆柱。

师：测量一下，这时圆柱的高度与圆锥的高度有什么关系？

生18：圆锥的高度是圆柱高度的3倍。

师：看来，这个②号圆柱和圆锥的关系不一般。从这个实验中，你又获得了什么信息呢？

设计意图综述：圆锥体积的计算公式简单明了，如何让学生在获得这个公式的同时获得数学思想与方法，体会到数学学习的乐趣呢？荷兰数学教育家弗赖登塔尔曾说：“没有一种数学的思想，以它被发现时的那个样子公开发表出来。一个问题被解决后，相应地发展为一种形式化技巧，结果把求解过程丢在一边，使得火热的发明变成冰冷的美丽。”那圆锥体积公式的推导过程设计成什么样子，才能让学生体验到它被发现时的那个样子呢？

1.自主选择研究对象

圆锥与哪个立体图形关系最紧密？教学中教师充分尊重学生已有的知识经验，放手让学生于联系中寻找问题的切入点。在这个过程中，学生不仅培养了空间观念，还积累了遇到问题时主动把未知转化为已知的重要经验。事实上，数学上很多重要的发现就是从这种主动建立关系开始的。

2.自主设计操作实验

本节课的设计突出了学生学习的自主性。教学中，教师没有直接给出实验操作需要的器材，而是让学生自主选择。学生于思辨中逐步获得理性分析的经验，思维的深刻性也因此得到提升。

3.自主发现体积公式

在学生看来，公式的得出是一件很高深的事情，是只有数学家才能完成的重任。但在本节课中，教师大胆地鼓励学生发明公式，并主动抛出几个形式不同的公式，要求把公式这个“数”与圆锥这个“形”结合起来思考，培养学生的几何直观和发散思维能力。学生对圆锥体积的认识也不再浮于表面，更不是孤立的，而是动态的、立体的、有层次的，这样获取的知识才有更好的再生性。

三、讨论

人教版数学教材体系中，以公式形式呈现结论的知识点不多。在这为数不多的结论性知识的学习过程中，如何把结论还原成它最初发现时的本来面貌，让学生亲历数学知识发现的过程，体验数学思考、积极探究所获得的学习乐趣，并为以后的学习积累活动经验，都是值得我们好好花功夫去研究的。而这些研究本身很考验一线老师对这个问题最本质的认识。对于教材编写者，有没有可能在编制教材的时候，呈现一个过程相对完整的研究性学习范例呢？【此文系湖南省教育科学规划“十三五”课题“小学数学教师核心素养和能力建设研究”（课题批准号：XJK17BZXX023）阶段性研究成果】

（执笔：邓求平、杨枚、刘硕鹏、谢加文、王丽燕、徐旺、李闯）