光纤陀螺寻北启动误差抑制方法研究

马知瑶， 周一览

0 引 言

寻北定向技术的研究与产品开发，对国防现代化以及国民经济发展具有重要意义[1]。光纤陀螺(fiber-optic gyroscope,FOG)是基于Sagnac效应的全固态陀螺仪，具有耐冲击、灵敏度高、寿命长、功耗低、集成可靠等优点，特别适合寻北定向系统的应用[2]。静态测量法是目前的主要寻北手段[3]，四位置寻北法因其寻北结果受光纤陀螺零偏及标度因数误差的影响较小而广泛采用[4]。

光纤陀螺具有上电后输出数据在一段时间内存在较大漂移率，后续逐渐趋于稳定的现象[5],这种启动特性造成了光纤陀螺寻北的启动漂移，并在寻北应用的冷启动状态时形成了寻北启动误差，导致寻北精度降低。目前，国内光纤陀螺稳定段寻北精度可达0.04°～0.06°，但光纤陀螺启动段的寻北精度则降低至0.09°～0.1°[6]。

针对该问题，本文分析了光纤陀螺寻北启动误差的成因，通过数值仿真总结了其特性，提出了抑制该误差的新寻北方法，并进行了实验验证。实验结果表明：在光纤陀螺性能相同的情况下，新寻北方法能够显著抑制光纤陀螺寻北启动误差，提高光纤陀螺寻北精度。

1 四位置寻北法原理

如图1所示，N为北向，FOG-AXIS为光纤陀螺敏感轴，P1为被测方向所在位置，θ为P1与北向的夹角，P2，P3和P4与P1位置的夹角分别为90°，180°，270°。

光纤陀螺在4个测量位置的理想输出Gi(i=1,2,3,4)分别为

图1 四位置寻北法示意

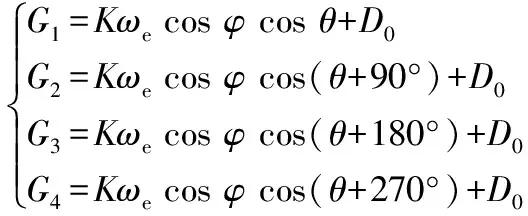
(1)

式中K为光纤陀螺标度因数；ωe为地球自转角速度；φ为测量点的地理纬度；θ为被测方位角，即被测方向与真北方向的夹角；D0为光纤陀螺零偏。推导出被测方位角

(2)

2 光纤陀螺寻北启动误差及其特性

典型的光纤陀螺输出数据如图2所示。

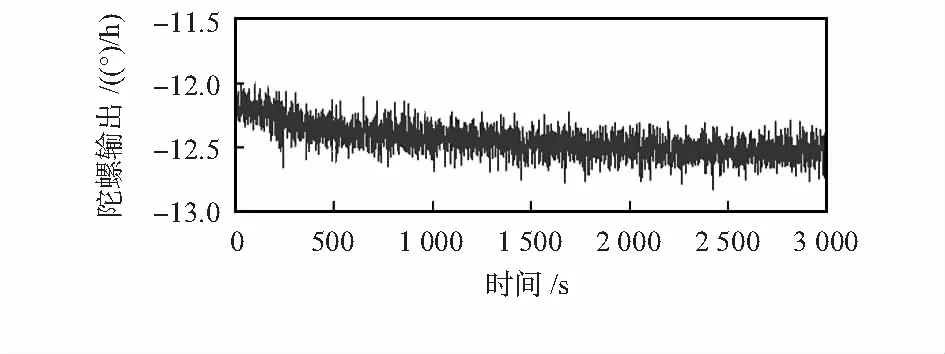
图2 包含启动阶段的光纤陀螺输出

(3)

(4)

从式(4)可以看出，被测方位角解算式中引入了与光纤陀螺漂移相关的ε4-ε2和ε1-ε3，造成了寻北结果的偏差，即为光纤陀螺寻北启动误差。

设光纤陀螺漂移率为k，光纤陀螺在每个位置的采样时间为t，式(4)可改写为

(5)

令G4-G2=A，G1-G3=B，则线性漂移特性下光纤陀螺寻北误差dθ为

(6)

式中A，B取决于被测方位角，而kt则取决于光纤陀螺漂移率。因此，光纤陀螺存在线性漂移时寻北误差与光纤陀螺漂移率和被测方位角相关。

1)分析陀螺漂移率对寻北误差的影响。仿真参数如下：4个位置的采样时间均为60 s，纬度30°，被测方位角为90°。光纤陀螺漂移率在(0°/h～3°/h)区间变化的寻北仿真结果如图3所示。

在新时期发展背景下，我国市场经济竞争越来越激烈，企业在发展过程中不断接受更加高难度的挑战，以此稳定企业的发展。在参与市场竞争过程中，企业领导能够发现会计成本核算的重要性。从会计成本核算角度来说，会计成本核算进行工作时，会计人员的专业素养越高，越能够提升成本核算的正确率，从而能够帮助企业获得经济利益最大化，以此促进企业快速发展。并且，企业进行会计成本核算工作，主要是对企业日常花销进行统计，在实际发展中应以此为基础不断改进企业规定，降低成本消耗，从而提升经济利益。因此，会计成本核算在企业发展中占有重要地位。

可知，在固定的方位角下，光纤陀螺寻北误差与光纤陀螺漂移率成正比。

2)分析方位角与寻北误差的关系。仿真参数如下：4个位置的采样时间均为60 s，纬度30°，光纤陀螺漂移率为1°/h。方位角在圆周内间隔1°依次变化的寻北仿真结果如图4所示。

图4 寻北误差与被测方位角关系

可以看出：线性漂移特性下，光纤陀螺寻北误差与方位角相关，在方位角45°和225°左右寻北误差最小，而在方位角135°和315°左右寻北误差最大。

综合仿真结果可知:在同等条件下，光纤陀螺寻北启动误差与光纤陀螺漂移率成正比；光纤陀螺寻北启动误差与方位角相关，呈现为2π周期的正弦分布。

3 寻北启动误差抑制方法

在现有的技术水平和制造工艺的条件下，要提高光纤陀螺硬件性能需要较高的代价，甚至无法实现[7]。本文在传统四位置寻北法的基础上，提出了改进的四位置寻北法。新方法将原方法中的4次采样改成8次减半时间采样，如图5所示，在不减小采样时间且不增加转位时间的前提下，可以有效抑制寻北启动误差，提高寻北精度。

图5 改进四位置方法编排示意

可以看出，改进四位置方法与传统四位置方位在采样和转位编排上有差异，但总采样时间和总转动角度相同。

不考虑寻北过程中占比较短的转位时间，当每个位置采样时间为t0时，传统四位置方法的编排中下，由线性漂移造成的式(3)中的εi为

(7)

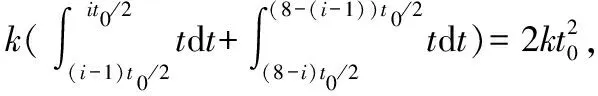
i=1,2,3,4

(8)

可以看出，虽然εi均不为零，但理论值相同，因此，ε4-ε2和ε1-ε3均为零，可以消除寻北结果计算的偏差，达到提高寻北精度的效果。

4 验证实验及结果分析

为验证改进寻北方法对光纤陀螺寻北启动误差的抑制效果，利用启动特性如图2所示的光纤陀螺，分别用四位置法和改进四位置法进行了寻北对比实验。光纤陀螺置于转台上，输入轴垂直于转台转动轴保持水平安装。在圆周内等间隔地取36个方位，每个方位上进行7次寻北实验，实验中，每个位置总采样时间为60 s。

实验过程中，不同的方位上，寻北实验开始前光纤陀螺均断电静置2 h后再重新上电，以保证光纤陀螺在不同的方位上的寻北实验均存在相同的启动过程。实验结果如图6、图7所示。

图6 2种方法首次寻北误差对比

图7 2种方法寻北精度对比

如图6所示，四位置法下光纤陀螺启动阶段寻北误差大小与寻北方位角相关，呈周期为2π的正弦分布，在45°和225°附近最小，实验结果与仿真结果一致，而改进四位置法在光纤陀螺启动阶段的寻北误差与方位角无相关性，新方法首次寻北误差(0.031°)与四位置法(0.159°)相比降低了80 %，使得光纤陀螺启动阶段寻北误差与稳定阶段寻北误差相当，基本消除了光纤陀螺寻北启动误差。

图7中，四位置法寻北的后6次，即稳定段平均寻北精度较高，但由于首次寻北误差较大，导致总体寻北精度较差且与方位角相关。新方法在消除了光纤陀螺寻北启动误差之后，总体寻北精度与后6次的寻北精度相当，且与四位置法的稳定段寻北精度相比未降低，进一步表明本文提出的新方法能够消除光纤陀螺寻北启动误差，提高光纤陀螺寻北精度。

5 结 论

光纤陀螺启动阶段的输出漂移导致了光纤陀螺寻北启动误差。本文提出了改进四位置寻北方法，可以在不增加寻北时间的前提下，得到更准确的寻北结果。实验数据表明：本文提出的新方法能够消除光纤陀螺寻北启动误差，提高光纤陀螺寻北精度。将此方法应用于工程实践，能在同等光纤陀螺性能基础上，有效提升光纤陀螺寻北性能，具有较高的工程应用价值。

参考文献:

[1] 管 斌，王成宾.序贯抗差估计在旋转调制陀螺寻北中的应用[J].传感器与微系统， 2014,33(12):158-160.

[2] 贾 明,杨功流.基于光纤陀螺的二位置快速寻北系统设计[J].传感器与微系统,2012,31(3):133-135.

[3] 王海明，张卫侠，李四海.基于FFT的陀螺寻北仪误差补偿[J].传感器与微系统，2004,33(2):32-34.

[4] 郑秋丽.光纤陀螺寻北仪误差分析及补偿技术研究[D].哈尔滨：哈尔滨工程大学,2011.

[5] 王立冬,王夏霄,张春熹.光纤陀螺寻北仪多位置寻北误差分析[J].压电与声光,2007,29(1):42-44.

[6] 周一览.过调制技术在光纤陀螺寻北中的应用[J].浙江大学学报:工学版,2015,49(9):1817-1820.

[7] 李绪友,王 爽,张 琛.光纤陀螺寻北仪四位置寻北算法的改进[J].仪器仪表学报,2009,30(6):759-763.