水下潜器系统导管螺旋桨水动力特性及周围流场分布预报与分析

吴家鸣，赖宇锋，李江伟，窦义哲，陈东军

（华南理工大学 土木与交通学院，广州 510640）

0 引 言

导管螺旋桨是一种常用的操纵水下潜器主动控制装置，水面控制人员通常通过脐带缆将控制信号发送到导管螺旋桨来实施对水下潜器的轨迹与姿态操纵[1-4]。准确地模拟水下潜器系统中导管螺旋桨周围的流场、螺旋桨盘面处的各种速度分量、桨叶所发出的推力分布特征以及这些速度与螺旋桨所发出推力的关系，有助于提高对于水下潜器系统中导管螺旋桨推力产生机理的了解与认识，从而为设计出操纵性能优良的水下潜器系统提供理论指导。

现有的技术在对水下潜器系统中导管螺旋桨水动力计算时，往往忽略水下潜器主体的影响，或者停留在仅仅分析在定常条件的单一方向来流下螺旋桨所产生的推力、转矩等水动力特性[5-7]。文献[8]中曾经对水下潜器系统中导管螺旋桨在水下潜器系统流场影响下的推力特性开展了研究。但是，由于这一计算方法是以定常手段来计算水下潜器系统进行直线运动时的推力特性，没有涉及导管螺旋桨在水下潜器系统非定常运动中水动力学问题。文献[9]采用了多重滑移网格技术来刻画水下潜器主体以及其它附属机构+导管螺旋桨构成的水下潜器系统转艏运动引起的摆动流场以及导管内由于螺旋桨旋转而引起的旋转流场。作者利用这一技术从宏观的角度对比分析了水下潜器系统中水下潜器主体以及其它附属机构的流场对导管螺旋桨所发出的推力的影响；从水下潜器系统的整体视角去观察导管螺旋桨在水下潜器系统转艏摆动中与潜器系统其它机构流场相互作用下的推力特征。

目前，以数值模拟的方法从整体或宏观的角度对导管螺旋桨的产生推进力的机理的研究已经取得不少的进展[10-13]。然而，对于水下潜器系统中导管螺旋桨周围流场分布的预报、对导管螺旋桨周围流场与导管螺旋桨所发出的推力之间的关系分析关注不多。本文采用滑移网格技术对作为水下潜器的主要控制机构的导管螺旋桨在水下潜器系统做转艏运动的工况下，导管螺旋桨的推力、螺旋桨周围的流场特性进行观察，对导管螺旋桨盘面处的各种速度分量沿盘面的分布以及桨叶切面所发出的推力与这些速度分量之间的关系进行观察。

1 控制方程、几何模型和计算域

1.1 控制方程

本文分析中设定流体为不可压缩流体，则水下潜器系统周围流场的控制方程为[14]：

（1）连续性方程

（2） 动量方程

式中：ui，uj为速度分量时均值 （i，j=1，2，3）；P 为压力时均值；ρ为流体密度；t为时间；μ 为流体粘性系数；gi为重力加速度分量为雷诺应力项。

1.2 几何模型

本文所分析的水下潜器系统为一主体为立式的对称翼型壳体结构，对称翼型壳体结构上方装设了二个鱼雷状浮体为航行中的水下潜器提供回复力矩，浮体尾部设置了用于水下潜器系统姿态控制的ka 4-70/19A导管螺旋桨，二浮体以及浮体与主体之间以翼型结构连接，图1为用于本文数值模拟计算的水下潜器系统及导管螺旋桨几何模型。表1为水下潜器系统主要尺度，导管螺旋桨的具体参数见表2。

1.3 计算域的构建

本文计算采用FLUENT求解器来求解水下潜器系统在转艏运动过程中系统周围流场的控制方程，在计算过程中选取RNG k-ε湍流模型，采用有限体积法离散控制方程和湍流模型。为了对所分析的水下潜器系统中导管螺旋桨周围流场分布及其与推力进行数值计算，本文构造了三个相互耦合的计算域：计算域Ⅰ、计算域Ⅱ和计算域Ⅲ。

图1 水下潜器系统及导管螺旋桨几何模型Fig.1 Geometrical model of underwater vehicle and ducted propellers

表1 水下潜器系统主要尺度Tab.1 Primary parameters of the underwater vehicle

表2 导管螺旋桨主要参数Tab.2 Primary parameters of the ducted propeller

表3 各子计算域之间的边界条件Tab.3 Boundary conditions of the computational domains

计算域Ⅰ所包含的是以导管内由于螺旋桨旋转而引起的旋转流场。该计算域所包含是以螺旋桨轴为轴心、长度等于导管长度、外周边界等于103%螺旋桨直径、旋转速度等于螺旋桨转速的圆柱形回转体旋转流场。

计算域Ⅱ所包含的是由于包括导管螺旋桨在内的水下潜器系统转艏摆动引起摆动流场。该计算域所包含以水下潜器系统坐标垂向坐标轴为其轴线，其半径包含了所计算整个水下潜器系统的圆柱形摆动流场。

计算域Ⅲ为一个长度方向与来流速度平行的长方体计算域。计算域刻画了包括计算域Ⅰ与计算域Ⅱ在内的外部流场的流动状态。计算域Ⅲ沿长度方向的中心轴线通过水下潜器系统的重心、并与计算域Ⅱ的圆柱形摆动流场的轴线垂直，水下潜器系统可以绕计算域Ⅱ的垂直轴线旋转。长方体计算域Ⅲ的长×宽×高的尺度根据计算精度与计算时间的综合平衡因素来决定。

计算域Ⅰ、Ⅱ之间以及计算域Ⅱ、Ⅲ之间的交界面通过interface技术进行耦合将它们组合为一个整体，通过这样一种方式构成为一个整体组合计算域的外围边界即为计算域Ⅲ的外围边界。表3给出了文中各子计算域之间的边界条件基本参数，表4给出了计算中三个计算域的主要尺度，图2给出了计算中所使用的计算域，计算中水下潜器系统转艏角的定义如图3所示。

图2 计算中所使用的计算域Fig.2 Computational domain applied in computation

图3 螺旋桨转艏角定义Fig.3 Definition of ducted propeller yawing angle

2 数值模拟与计算结果分析

采用滑移网格技术计算导管螺旋桨推力特性的可靠性，本文作者已经通过将计算结果[8]与实验室模型实验结果[15]的对比得到证明。本节以水下潜器系统中右导管螺旋桨为观察对象，对在水下潜器主体及其它附属机构流场影响下导管螺旋桨周围流场、导管螺旋桨盘面处的各种速度分量以及推力沿盘面的分布以及桨叶切面所发出的推力与这些速度分量之间的关系进行观察与分析，所观察的水下潜器系统如图1所示。计算中，水下潜器系统绕其垂向坐标轴以幅角为30°、周期为10 s作转艏摆动，其转艏摆动的表达式为：

式中：θ为转艏角，rad；t为时间，s。在水下潜器系统做转艏摆动的同时，左右导管螺旋桨以转速为1 200 rpm的外旋方式旋转，即右导管螺旋桨以顺时针方向正传、左导管螺旋桨以逆时针方向反转。计算中，对水下潜器系统在进行转艏摆动时相对于0.5 m/s均匀来流条件下导管螺旋桨的流场与推力特性进行了数值模拟和对比分析。

2.1 导管螺旋桨在转艏运动中的推力、平均进速与平均诱导速度变化特征

图4为正转的右导管螺旋桨在水下潜器组合体进行转艏摆动过程中的推力数值计算结果，曲线附近的箭头表示水下潜器系统转艏摆动的方向，文中图5～8中的箭头也表示与图4相同的含义。从图4计算结果的观察可以看出：对于相同的转艏角，当导管螺旋桨进行顺时针方向的转艏摆动时（从30°转艏至-30°），在水下潜器系统转艏摆动过程中的导管螺旋桨所发出的推力要大于逆时针方向的转艏摆动（从-30°转艏至 30°）。这是由于当水下潜器系统进行逆时针转艏摆动时，作为计算对象的右导管螺旋桨由于系统逆时针转艏摆动而引起了螺旋桨沿其轴线运动方向与来流方向相反，在来流与逆时针转艏摆动的综合影响下，螺旋桨盘面处所感受的进速要比进行顺时针转艏摆动时要大（见图5），此时在螺旋桨叶切面上所感受到相对来流合成速度的攻角较小，叶切面所产生的推力也较小；反之，当水下潜器系统进行顺时针转艏摆动时，叶切面所产生的推力将较大。在本文的计算中，进速定义为在导管螺旋桨进口盘面处的流体速度。

图4 转艏过程中右桨推力变化Fig.4 Thrust produced from the right ducted propeller in turning motion

图5 转艏过程中盘面处的进速Fig.5 Advance velocity on the propeller disk in turning motion

图6 转艏过程中盘面处的轴向诱导速度Fig.6 Axial induced velocity on the propeller disk in turning motion

图6～8给出了在图4相同的工况中在所计算的导管螺旋桨盘面处的轴向、周向与径向诱导速度平均值Va、Vc和Vr，在图7和图8中的Vc和Vr值取自盘面后35 mm处，Va由下式确定：

其中：Vab和Vaf分别取自导管进、出口处相同径向半径和相同周向位置的轴向流速。

对比图4～8在水下潜器系统转艏摆动过程中所表现出的水动力现象计算结果可以发现：就导管螺旋桨的整体平均效应而言，导管螺旋桨所发出的推力与螺旋桨盘面处的平均进速相关。平均进速越小，螺旋桨所发出的推力越大；诱导速度与推力之间的关系不明显；轴向与周向分量是诱导速度的主要成分，而径向诱导速度所占的份量较少。

图9给出了在进行顺时针方向的转艏摆动时，当水下潜器系统摆动至转艏角θ分别为30°、0°和-30°时，螺旋桨旋转一周时间段内所发出的推力的时间历程。从图9的结果中可以看到：（1）不论是在哪个转艏角条件下，螺旋桨每旋转一周，推力均出现了四次振荡峰谷值。这是由于本文所分析的导管螺旋桨为一个四叶桨，螺旋桨每旋转一周，其四个桨叶都会相继旋转至同一辐角，由此而表现出了一种旋转一周出现四次峰谷值状态。（2）对应于不同的转艏角，螺旋桨旋转一周表现出了相异的推力幅值特征：螺旋桨旋转一周所发出的推力平均值当转艏角θ=30°时最大、θ=0°时次之，而θ=-30°时最小。其变化规律与图4的结果一致。

图9 右导管螺旋桨一个周期内推力变化Fig.9 Thrust from the right ducted propeller in one revolution

2.2 进速与诱导速度、推力沿盘面的分布特征

图10～14给出了水下潜器系统转艏至 θ=30°、θ=0°和 θ=-30°，当其中一个桨叶旋转至相位角φ=0°时螺旋桨所产生的推力、进速和三个方向的诱导速度周向平均值沿桨叶相对半径Rr分布的计算结果。通过图10～14的计算结果，可以观察到在水下潜器系统导管螺旋桨所发出推力与进速、诱导速度各种分量沿桨叶径向的分布特征以及推力与各种速度分量之间的关系。桨叶在导管螺旋桨系统中的相位角定义如图15所示，桨叶相对半径Rr的定义为：

其中：R为螺旋桨梢圆半径、r为叶切面所处的径向半径。从图10～14的计算结果可以看出，推力、进速和诱导速度各种分量沿桨叶径向的分布有以下特征：

图10 推力沿桨叶径向的分布Fig.10 Thrust distribution along the radial direction of the blade

图11 进速沿桨叶径向的分布Fig.11 Advance velocity distribution along the radial direction of the blade

（1）水下潜器系统旋转至不同的转艏角，推力和各种速度分量沿桨叶径向的分布的趋势大致相似，推力和速度分量在不同的转艏角下的分布特征差异很小。

（2）螺旋桨所发出的推力以分布在叶梢部分为主，越接近叶根，推力分量所占的份额越少；而在相对半径Rr=1时，单位长度上推力分布达到最大值。

（3）不同性质的速度分量沿桨叶的径向表现出不同的分布特征：螺旋桨盘面进速沿桨叶的径向呈现一种大致均匀分布的特点；轴向诱导速度沿桨叶径向大致为均匀分布，但在叶梢部分，随着相对半径Rr的增大，轴向诱导速度分量急速降低；周向诱导速度分量在大相对半径部分的分布比小相对半径要大；相对于轴向和周向诱导速度，径向诱导速度分量的数值较小。

（4）在叶梢部分轴向诱导速度分量沿径向分布快速减少的原因是由于导管螺旋桨后尾流收缩以及导管与螺旋桨叶梢部分的耦合作用而在桨叶前后所产生的旋涡而造成的。

图12 轴向诱导速度沿桨叶径向的分布Fig.12 Axial induced velocity distribution along the radial direction of the blade

图13 周向诱导速度沿桨叶径向的分布Fig.13 Circumferential induced velocity distribution along the radial direction of the blade

图14 径向诱导速度沿桨叶径向的分布Fig.14 Radial induced velocity distribution along the radial direction of the blade

图15 桨叶的相位角定义Fig.15 Phase angle of the propeller blade

图16给出了水下潜器系统转艏至θ=30°、θ=0°和θ=-30°时，导管螺旋桨其中一个桨叶幅角φ从0°→360°顺时针旋转一周时推力沿螺旋桨盘面的分布，从图中的结果我们可以观察到螺旋桨旋转时推力沿桨叶的径向分布以及沿周向的分布特征。从图16的计算结果，可以观察到桨叶所发出的推力有以下的一些特点：

（1）就本文所讨论的导管螺旋桨而言，无论水下潜器系统处于怎样的一种转艏角状态，桨叶上的推力分布主要集中在叶梢部分，叶根部分产生的推力份额很少；相对半径Rr越大，沿桨叶径向单位长度上的推力分布密度就越大，在相对半径的Rr=0.8～1.0叶梢部分的推力成分约占整个桨叶推力总额的50%左右，在Rr=0.9～1.0部分的推力成分约占推力总额的30%左右，而在Rr≤0.8部分推力分布所占的份额很少。

（2）水下潜器系统摆动至不同的转艏角，推力沿导管螺旋桨盘面的分布表现出相异的分布特征。θ=30°时，推力分布由大到小依次为：第四、第二、第三、第一象限；θ=0°时，推力分布由大到小依次为：第四、第一、第三、第二象限；而θ=-30°时，则桨叶从第三象限的推力最小值、突变到第二象限时的最大值、再依次经过第一、第四象限逐步变小。这种现象表明：桨叶在φ=0°→360°一周旋转中，所发出的推力经历了一种大小波动的变化过程。

图16 推力沿盘面的分布Fig.16 Thrust distribution along the propeller disk

2.3 导管螺旋桨周围流场分布及推力特性成因讨论

从本文的计算结果可观察到：水下潜器系统中的导管螺旋桨在其转艏摆动中的水动力特性呈现几个特点：（1）推力沿桨叶径向的分布主要集中于叶梢；（2）经过盘面后从导管流出的尾流有一种明显沿径向向轴心收缩的倾向；（3）轴向诱导速度在桨叶大相对半径处迅速减小。

作者认为，产生这些现象的主要原因是在于导管与螺旋桨叶梢部分的耦合作用而在桨叶叶面前后所产生的梢涡、导管螺旋桨本身的结构特征所致。梢涡的大小、接近叶面的程度和梢涡的演变过程都对导管内螺旋桨周围的流场特征以及推力特性有一定的关联；叶背（低压面）、叶面（高压面）在叶梢部分旋涡的产生、扩展，是引起导管螺旋桨盘面后尾流的收缩，从而导致轴向诱导速度在叶梢部分的比重降低的一个诱因。图17为转艏角θ=0°时螺旋桨梢部漩涡数值计算结果。

图17 螺旋桨梢部漩涡Fig.17 Vortices at the blade tip

本文的计算分析表明，由于叶面、叶背在叶梢部分梢涡形成和发展过程的差异，由这些梢涡在叶面、叶背所产生的流场和压力场也不同。图18为当水下潜器系统摆动至转艏角分别为θ=-30°、0°、30°时，作为计算对象的右导管螺旋桨内部叶梢、导管以及它们之间间隙部分的局部流线分布图。从图18的计算结果可以看出：在不同的转艏角下，尽管在叶梢部分的叶面与叶背部分分别形成了二个梢涡，但两者产生的机理、它们与桨叶所处的相对位置、以及所产生的力学效果并不相同。在叶背处产生的梢涡贴近桨叶，由此而形成了一个低压区；而在叶面处，由于梢涡不贴近桨叶，因此在叶面处形成了一个相对于比叶背压力高的高压区。

图18 在不同的转艏角下叶梢部分梢涡局部流线图Fig.18 Streamline distribution of vortices at the blade tip under different turning angle

在图18中还可以注意到，由于梢涡在叶面后的扩展，引起了螺旋桨尾流的收缩，这种尾流收缩导致了叶面后轴向诱导速度在叶梢部分速度的大幅度降低、进而引起叶切面来流合速度矢量攻角的增大。这种由于梢涡在叶面后的扩展而导致的轴向诱导速度在叶梢部分的降低也进一步加大了叶面与叶背之间的压力差。

从上述的现象观察不难看出，由于叶梢部分产生的梢涡引起的叶面与叶背之间的压力差是导致桨叶的推力分布沿叶梢部分集中的一个重要原因。图19、20给出了在图18的条件下叶梢部分弦长方向切片压力分布图和沿桨叶不同相对半径处螺旋桨盘面前后在导管内的压力分布计算结果。在图20中，压力系数Cp、导管内轴向相对坐标x′分别为：

式中：Pb为叶切面计算点处的压力、P0为大气压力、ρ为水的密度、VA为导管进口处的平均进速、x、L分别为图21所示的导管内轴向位置坐标和导管长度。

图19 三种转艏角条件下右导管螺旋桨叶梢部分弦长方向切片压力分布图Fig.19 The pressure of tip blade slices along the chord directions under three turning angles

图20 三种转艏角条件下右导管螺旋桨盘面前后压力分布图Fig.20 Pressure distributions between the face and back of propeller blade under three turning angles

从图20的结果可以发现，在叶梢处螺旋桨盘面前后表现出了很大的压力差；而在相对半径Rr≤0.8的桨叶其它部分，螺旋桨盘面前后的压力差则大大地减小。综合图18-20的计算结果有以下的观察与结论：

（1）产生推力沿桨叶的分布主要集中于叶梢、轴向诱导速度在桨叶大相对半径处迅速减小等水动力现象的一个重要原因在于导管与螺旋桨叶梢部分的耦合作用而在桨叶叶面前后所产生的梢涡所致。梢涡的大小、接近叶面的程度和梢涡的演变过程都对导管内螺旋桨周围的流场特征以及推力特性有一定的关联。在叶梢处，由于图18所示的叶背旋涡的作用，螺旋桨尾流收缩现象明显。由此而导致了轴向诱导速度的降低、叶切面来流攻角的增大。这些现象都成为了引起推力分布向叶梢部分集中的一个主要原因。

（2） 根据图 20 的计算结果，转艏角分别为 θ=-30°、0°、30°时，桨叶在不同的相对半径处叶面与叶背之间的压力系数差值如表5所示。由表5的结果不难发现，在三种转艏角下，压力差最大值均发生在叶梢处，随着桨叶相对半径的减小，叶面、叶背之间的压力差值也逐步减低；比较三种不同的转艏角，沿桨叶不同相对半径处压力差由小到大依次为：θ=-30°、0°、30°。不难看出，也正是由于导管螺旋桨叶盘面前后梢涡在转艏角不同时所引起的压力差分布的差异，成为了图9中不同转艏角下导管螺旋桨所发出的推力平均值不一致的主要原因。

图21 导管与螺旋桨坐标示意图Fig.21 Coordinate of duct and propeller

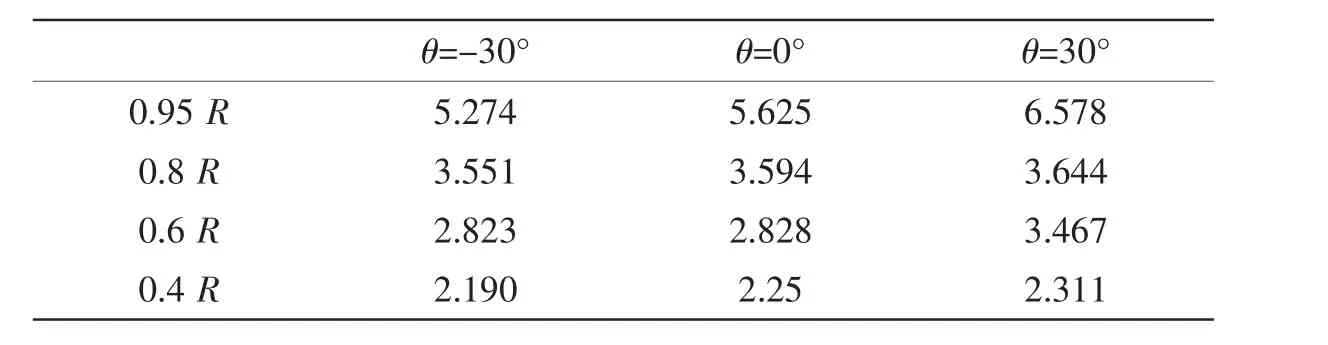
表5 不同半径处叶面与叶背之间的压力系数差值Tab.5 Pressure coefficients difference between face and back of the blade at different radii

3 结 论

对于本文所研究的水下潜器系统中的导管螺旋桨，其周围流场与推力分布存在着以下特征：

（1）水下潜器系统中的导管螺旋桨所发出的推力与螺旋桨盘面处所感受的进速相关。对于给定的相对半径处叶切面，在一定的螺旋桨转速条件下，进速越小，螺旋桨所发出的推力越大。

（2）本文所研究的导管螺旋桨桨叶上的推力分布主要集中在叶梢部分，相对半径越大，沿桨叶径向单位长度上的推力分布密度就越大，在相对半径大于0.9的叶梢部分，其推力成分约占整个桨叶推力总额30%左右，而在叶根部分推力分布所占的份额很少。

（3）产生推力沿桨叶的分布主要集中于叶梢的主要原因在于叶梢部分在桨叶叶面前后所产生的梢涡所致。在叶梢处，由于叶背旋涡的作用，螺旋桨尾流收缩现象明显。由此而导致了轴向诱导速度的降低、叶切面来流攻角的增大，叶切面压力面和吸力面之间压力差增大，从而引起推力分布向叶梢部分集中。

[1]Avila JPJ,Adamowski JC.Experimental evaluation of the hydrodynamic coefficients of a ROV through Morison’s equation[J].Ocean Engineering,2011,38:2162-2170.

[2]Jaulin L.Robust set-membership state estimation;application to underwater robotics[J].Automatica,2009,45:202-206.

[3]Li JH,Jun B H,Lee PM,et al.A hierarchical real-time control architecture for a semi-autonomous underwater vehicle[J].Ocean Engineering,2005,32:1631-1641.

[4]陈 健,吴家鸣,徐,等.立式翼型主体拖曳式水下潜器的设计及操纵性能[J].海洋技术学报,2015,34(4):1-6.Chen Jian,Wu Jiaming,Xu Ying,et al.Study on design and control performance of the underwater towed vehicle with verticle airfoil main body[J].Journal of Ocean Technology,2015,34(4):1-6.

[5]Fang M C,Hou CS,Luo H JH.On the motions of the underwater remotely operated vehicle with the umbilical cable effect[J].Ocean Engineering,2007,34:1275-1289.

[6]吴家鸣,崔 寅,邓 威,等.控制动作下的带缆遥控水下机器人水动力特性分析[J].华南理工大学学报(自然科学版),2012,40(4):150-157.Wu Jiaming,Cui Yin,Deng Wei,et al.Hydrodynamic characteristics of tethered underwater robot under control manipulations[J].Journal of South China University of Technology(Natural Science Edition),2012,40(4):150-157.

[7]吴家鸣,郁 苗,朱琳琳.带缆遥控水下机器人水动力数学模型及其回转运动分析[J].船舶力学,2011,15(8):827-843.Wu Jiaming,Yu Miao,Zhu Linlin.A hydrodynamic model for a tethered underwater robot and dynamic analysis of the robot in turning motion[J].Journal of Ship Mechanics,2011,15(8):827-843.

[8]吴家鸣,邓 威,赖华威.回转状态下导管螺旋桨水动力特性的数值模拟[J].华南理工大学学报(自然科学版),2010,38(7):90-96.Wu Jiaming,Deng Wei,Lai Huawei.Numerical simulation of hydrodynamic characteristics of ducted propeller in turning motion[J].Journal of South China University of Technology(Natural Science Edition),2010,38(7):90-96.

[9]吴家鸣,叶志坚,金晓东,张城玮,徐.水下潜器导管螺旋桨在转艏摆动中的推力特性分析[J].华南理工大学学报(自然科学版),2015,43(12):141-148.Wu Jiaming,Ye Zhijian,Jin Xiaodong,Zhang Chengwei,Xu Ying.Analysis of thrust characteristics of ducted propellers in underwater vehicle with yawing motion[J].Journal of South China University of Technology(Natural Science Edition),2015,43(12):141-148.

[10]Wu JM,Yu M,Zhu L S.Trajectory and attitude control of a tethered underwater robot[C]//Proc.of the 20th Int.Offshore and Polar Eng.Conf.Beijing,China,2010,1:287-294.

[11]Castro A M,Carrica PM,Stern F.Full scale self-propulsion computations using discretized propeller for the KRISOcontainer ship KCS[J].Computers&Fluids,2011,51:35-47.

[12]Wu JM,Lai H W,Zhu L S.A practical numerical method to forecast the hydrodynamic behavior of a ducted thruster in the flow field of a tethered underwater robot[C]//Proc.of the 19th Int.Offshore and Polar Eng.Conf.Osaka,Japan,2009,2:710-715.

[13]叶志坚,吴家鸣,张城玮,徐.水下潜器系统中导管盘面流场分布与螺旋桨推力特性关联性分析[J].广东造船,2015,34(5):22-25.Ye Zhijian,Wu Jiaming,Zhang Chengwei,Xu Ying.Analysis on the relevance between disk flow field distribution and thrust of ducted propeller in underwater vehicle system[J].Guangdong Shipbuilding,2015,34(5):22-25.

[14]Versteeg H K,Malalasekera W.An introduction to computational fluid dynamics:The finite volume method[M].Wiley,New York,1995:49-54.

[15]Spry SC,Empey D M,Webster W C.Design and characterization of a small-scale azimuthing thruster for a mobile offshore base module[J].Marine Structures,2001,14:215-229.