基于数值计算方法的矢量合成射流激励器推力特性研究

耿令波 ， 衣瑞文 ， 林 扬 ， 胡志强 ， 王 超

（1.中国科学院大学，北京 100049；2.机器人学国家重点实验室，中国科学院沈阳自动化研究所，沈阳 110016）

0 引 言

传统的水下机器人依靠螺旋桨与舵的配合实现操纵控制，在低速航行状态下舵效较差，无法实现高机动性，提高机动性的一种常见解决方案是设置多部推进器构成矢量布置，但这样会影响机器人的流体动力外型。为了在不影响流体动力性能的前提下，提高低速状态下机器人的机动性，必须采用新的姿态调节方式。

自然界存在许多依靠射流获取动力的生物，如章鱼，这些生物通过将吸入体内的流体快速喷出而获得所需的动量。在船舶上广泛采用的喷水推进器也属于射流驱动，喷水推进器所形成的射流其方向、流量及速度均是恒定的，属于稳态射流；而章鱼等水生生物所形成的射流其速度、流量均是时刻改变的，一般称为非稳态射流。

关于非稳态射流的研究发现射流中涡的出现可以明显提高推进效率[1-3]，Krueger[1]通过实验发现涡的产生使得射流推力提升20%以上，Ruiz等[2]的实验结果显示相较于稳态射流，含有涡的非稳态射流使得推进效率提升40%，且与阻力相关的水动力性能提升70%以上。

合成射流也是一种非稳态射流，通过激励器作动部件的周期往复运动来改变其内部体积，进而实现对周围环境流体的吸入/排出。激励器只有一个口与外部环境联通，其吸入与排出的流体流量完全相同，因而合成射流是一种零质量射流，对外部环境具有零质量效应。

合成射流最初作为一种流体主动控制技术广泛应用于航空领域[4-5]，合成射流驱动器体积小、质量轻、结构简单，且可以完全集成在机器人本体内部，对机器人流体外型影响很小，非常适合水下机器人低速状态下的姿态控制，因而，作为一种新型的驱动和姿态调节方式，水环境下的合成射流正受到越来越多的关注和研究。

Krieg等[6]设计了一种活塞型合成射流推进器，并对该合成射流推进器进行了一系列推力实验，实验结果显示，虽然合成射流在一个周期内的质量变化为0，但其动量变化不为0，可以产生净推力，证明了合成射流用于水下推进、姿态调节的可行性。Krieg和Mohseni[7]设计了一种依靠合成射流进行姿态调节的水下机器人-CALAMAR-E，并对其进行了姿态控制实验，实验结果显示在合成射流激励器的调节作用下，CALAMAR-E可以实现2.23 r/min的转动速度，验证了合成射流激励器在水下机器人姿态调节方面的有效性。

目前，合成射流激励器的出口方向大都是不可调的，这样要实现多自由度的运动调节，需要安装多个激励器，无疑会增加机器人的尺寸。为了解决此问题，本文设计了一种矢量合成射流激励器，该激励器的出口是柔性的，通过线驱动实现激励器出口偏角在空间各个方向上的调节，进而实现激励器作用力的矢量控制。建立了激励器出口偏转控制的数学模型以及激励器作用力的数学模型，并采用数值计算方法对该矢量合成射流激励器在出口具有不同偏转角度时的流场进行了数值计算，给出了作用力随偏角改变的变化规律，并结合本文建立的数学模型揭示了激励器作用力的变化机理。

1 矢量合成射流激励器

1.1 结构设计

本文设计的矢量合成射流激励器如图1所示，包括激励器主体及偏角可控的柔性出口。激励器主体包括驱动电机、偏心轮、连杆及活塞，通过偏心轮的转动实现活塞的往复运动。可偏转出口主要由驱动电机、骨架弹簧、间隔盘、柔性橡胶管及驱动线组成，其结构如图2所示。间隔盘的作用是保证出口各部分受力均匀，进而实现近似圆弧的平滑弯曲。三组驱动线按照120度的间隔均匀分布，通过控制三组驱动线的长度即可改变激励器出口在各个方向上的偏转，进而实现激励器推力方向的调节。

图1 矢量合成射流激励器Fig.1 Structure of the vectored synthetic jet actuator

图2 激励器柔性出口Fig.2 The components of flexible nozzle

1.2 激励器出口偏转数学模型

为了实现对激励器偏转角度的准确控制，必须建立各驱动线长度变化与激励器出口偏角的数学关系，即建立激励器出口偏转的运动学模型。

建立基坐标系O-XYZ及末端坐标系O′-X′Y′Z′，基坐标系位于激励器出口与激励器主体连接处，末端坐标系位于喷口位置，如图3所示。将三组驱动线在基坐标系及末端坐标系的安装孔分别定义为 P1、P2、P3及 P1′、P2′、P3′，为了计算方便，将 OP1及 O′P1′分别定义为各自坐标系的 X 轴。P1′、P2′、P3′在末端坐标系的坐标及P1、P2、P3在基坐标系的坐标，可分别表示为：

图3 运动学参数定义Fig.3 Kinematics of the flexible nozzle

激励器出口的弯曲可看作是绕广义轴OM的弯曲，假设OM与基坐标系Y轴的夹角为β，激励器出口的弯曲角度为θ，各参数定义如图3所示。可通过β与θ这两个参数来描述末端坐标系与基坐标系间的姿态变换：

由于间隔盘的作用，激励器出口在弯曲时，各部分的受力比较均匀，因而，弯曲后激励器出口可当圆弧处理，如图4所示。可根据出口偏角θ以及驱动线在基坐标系与末端坐标系安装点之间的长度li求出此时驱动线长度Li的值：

第i驱动线在基坐标系及末端坐标系安装点 Pi、Pi′之间的距离 li可表示为：

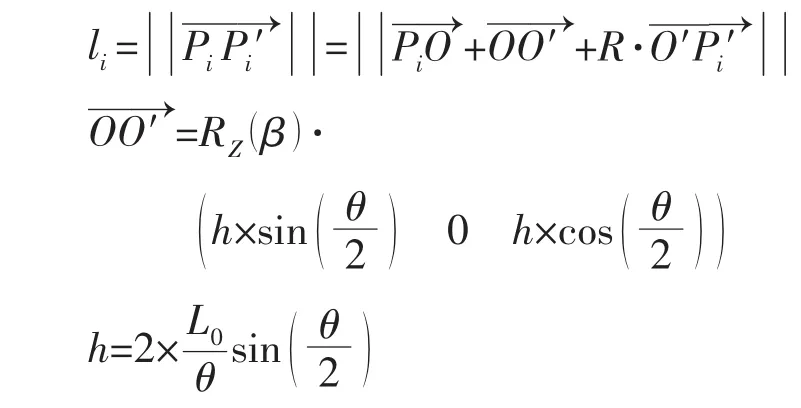
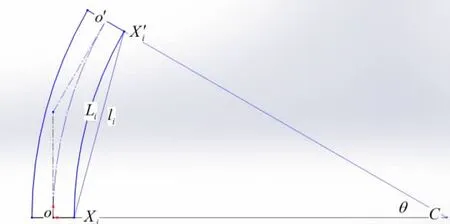
图4 出口弯曲的圆弧近似Fig.4 Circular approximation of the bending of the nozzle

式中）为旋转变换矩阵，表示绕Z轴旋转β角，h表示基坐标系平面与末端坐标系平面之间的距离，即表示基坐标系与末端坐标系之间的变换矩阵，定义如前文；L0表示出口未弯曲前的高度，由于是等曲率弯曲，因而弯曲后中心圆弧（即图4中虚线所示圆弧）的长度也是L0。将li的表达式带入Li便可求出各驱动线长度与激励器出口偏角的数学关系，即激励器出口的运动学模型。由该运动学模型，通过控制各驱动线的长度即可控制激励器出口的偏转角度，进而实现激励器推力的矢量控制。

2 数值计算方法

2.1 数值方法

为了研究激励器出口偏转角度对其作用力的影响，本文采用数值计算方法对激励器出口具有不同偏转角度时的流场进行数值计算。目前关于水下合成射流的研究大都集中在实验方面，数值计算方面的研究相对较少，Li[8]采用fluent软件的动网格算法对合成射流激励器的流场进行了数值计算。Thomas[9]采用CFX软件对一种合成射流激励器在不对称激励函数作用下的流场进行了数值仿真，Kumar等[10]在fluent软件中采用大涡模拟对三维射流激励器进行了数值仿真。

合成射流本质上属于一种湍流现象，对湍流的数值计算一般包括直接模拟，大涡模拟及雷诺时均方程，直接模拟与大涡模拟计算量很大，限于现有的计算机硬件条件，本文采用雷诺时均方程进行数值模拟。对三维不可压粘性流动，其雷诺时均N-S方程为：

式中为时均速度，ui′为脉动速度为雷诺应力。按照不同的封闭形式，雷诺时均方程又可分为单方程模型（Spalart-Allmaras），两方程模型（k-ε、k-ω）以及雷诺应力模型，本文采用剪切应力输运kω模型（SST k-ω）进行数值计算，该模型结合了近壁k-ω模型的稳定性和边界层外部k-ε模型独立性的特点，对自由来流的湍流度并不敏感，且该模型能适应压力场变化的各种物理现象。

SST k-ω湍流模型形式为，湍流强度k方程：

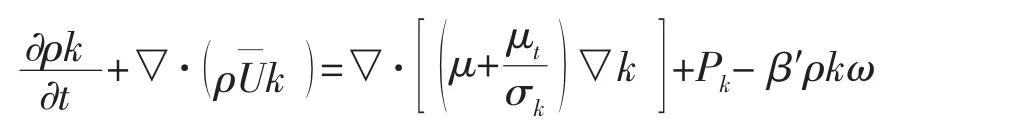
湍流频率ω方程：

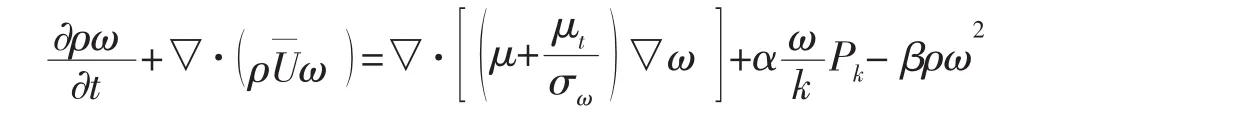
本文所研究的合成射流激励器的作动部件为活塞，活塞的运动指定为正弦型：

式中：y代表活塞位置，a表示活塞振幅，取为5 mm，f为活塞振动频率，取为10 Hz，t表示时间。为了尽可能接近物理实际，本文采用动网格对活塞运动进行模拟，激励器底部为动边界，其运动规律由（1）式决定，与底部活塞相邻的激励器主体定义为变形边界，变形边界的变形规律为动态分层，即当单元的高度大于某一设定值时，一个单元沿高度方向分裂为两个；当单元高度小于设定值时，两个单元在高度方向合并为一个单元，如下：

式中：hideal为网格高度设定值，h为网格高度当前值，αs为比例系数，Ei、Ei+1为分裂/合并前单元，Ej、Ej+1为分裂/合并后单元。

2.2 边界条件及网格划分

本文所采用的激励器为回转体结构，如图5所示，激励器的几何参数如表1所示，此参数是经过优化的最优值，在激励器出口直径一定的情况下，采用此组参数合成射流激励器的推进效率最高。

为了使边界对流动的影响最小，将外流域取得充分大，外流域的尺寸如表1所示，整个计算域如图6所示。本文采用基于动态分层技术的动网格模型对活塞的运动进行模拟，为了便于应用动态分层技术，将激励器底部网格划分为棱柱形网格，外流域及激励器出口划分为结构网格，过渡位置划分为非结构网格，外流域的网格划分如图6所示，激励器出口采用O型剖分。

流场边界条件设置如图6所示，激励器底部设置为动边界，激励器圆柱面设置为变形边界，激励器的其它边界均设置为无滑移壁面条件。与激励器出口相对的外流场边界设置为压力出口，与激励器出口相连的边界设置为无滑移壁面，其余边界设置为压力入口。

流场设置为三维、粘性、不可压和非定常，流体设置为海水，湍流模型采用SST k-ω模型，空间、压强和能量均采用二阶精度离散。为保证求解精度，每个周期划分为100个时间步，每个时间步长迭代120次。

为了探究激励器出口偏角对作用力的影响，在保证其他设置相同的条件下，按照15度间隔改变激励器的出口偏角，共7个算例，激励器偏角取值如表2所示。

图5 激励器几何参数及边界条件Fig.5 Parameter definition and the boundary condition of the actuator

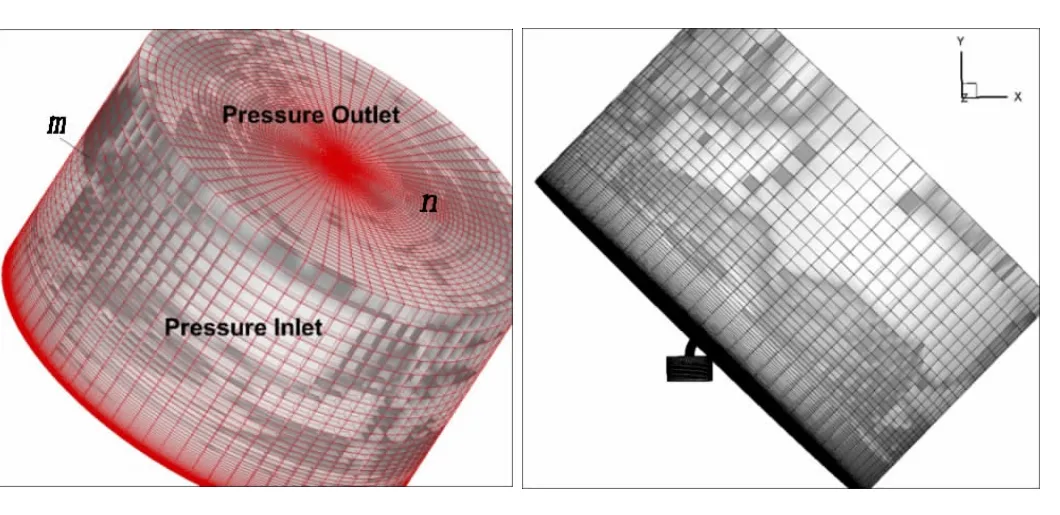
图6 外流场及边界条件Fig.6 The outflow field and the boundary condition

表1 激励器及外流场几何参数Tab.1 Geometrical parameters of the actuator and the out flow field

表2 不同算例的出口偏转角度Tab.2 The deflection angle of different cases

3 作用力数学模型

Krueger[1]为了研究非稳态射流高推进效率的作用机理，曾经建立用于描述非稳态射流作用力的数学模型，但该模型仅考虑射流喷出激励器的过程，没有考虑激励器吸入流体过程，而对于合成射流，吸入流体过程也会产生力的作用，因而Krueger建立的模型不能直接用于分析合成射流。

Thomas[11]也建立过合成射流的作用力模型，该模型以激励器外部流体为研究对象，通过作用力与反作用力的关系，将外部流体对激励器出口的作用力视为激励器产生的推力。这种建模方法忽略了激励器内部的流动，而实际上由于活塞的周期性往复运动，激励器内部流体会发生周期性的加减速，这种加减速会产生力的作用，因此，忽略激励器内部流动建立的模型是不精确的。

3.1 合成射流作用力模型

激励器的作用力是激励器边界与激励器内部流体进行相互作用时产生的，更加符合物理实际的建模方法应该是取激励器内部流体为研究对象。本文将激励器内部流体作为控制体，如图7所示。

与压强应力相比，合成射流激励器所受到的剪切（粘性）应力可以忽略不计。因此，激励器受到的作用力即为流体施加在激励器内表面的所有压强应力的合力，可以表示为：

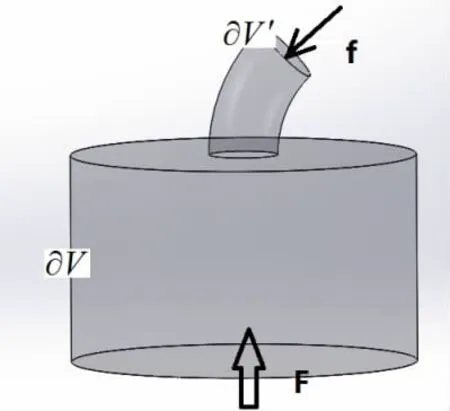
图7 所选取的控制体Fig.7 Control volume

式中]表示压强应力表示激励器的内表面，n表示激励器内表面的外法向。将（2）式对激励器内表面及激励器出口所组成的封闭曲面进行积分，可得到：

式中：A表示激励器出口，∂V′表示激励器内表面与激励器出口构成的封闭曲面。对（3）式右边应用高斯散度定理：

对整个控制体内的流体在Y方向应用动量定理：

由于不考虑重力、电磁力等体积力，并对其采用有限体积法进行积分得到：

上式左边表示整个控制体内的动量变化。对于合成射流来说，激励器内部的动量变化是由两部分引起的，一部分是激励器出口不断喷出或吸入流体，即由质量变化所引起的动量变化；另一部分是激励器作动部件所引起的流体加减速产生的动量变化，因此上式左边等价于：

式中：˙表示激励器出口的质量流量，即单位时间内流经激励器出口的质量，v表示流经激励器出口的流体的平均速度，表示控制体内等效的加速质量及加速度。

这样，合成射流激励器产生的作用力可以表示为：

式中：上式最右端一项代表的物理意义是激励器出口外部流体对控制体内流体施加的作用力，将其用f0表示，可改写为：

由（5）式可知，激励器产生的作用力由三部分组成，分别是激励器内部流体质量变化所产生的作用力，激励器内部流体加减速所产生的作用力，以及激励器外部流体对控制体内流体的作用力。

3.2 稳态射流作用力模型

合成射流为一种速度周期性变化的非稳态射流，与之相对的是速度大小及方向基本恒定的稳态射流，如螺旋桨及喷水推进器产生的射流。研究发现，合成射流相对于稳态射流具有推力增强效应[2-3]。

本文将具有相同质量流量的稳态射流的推力作为基准值，通过将合成射流推力与稳态射流推力进行对比，来比较不同条件下的合成射流的推力及推进效率。为此，本文下面建立稳态射流作用力的数学模型。

当射流为稳态射流时，此时由于流体没有加速，因此（4）式可简化为：

半个周期内的总动量为：

（6）式所以只对半个周期进行积分，是因为合成射流只有半个周期是喷出射流，另外半个周期是吸入射流过程，因而，为了保证合成射流与稳态射流的流量相同，只对其在半个周期进行积分。激励器活塞震动引起的激励器出口处的瞬时质量流量及瞬时流速可以表示为：

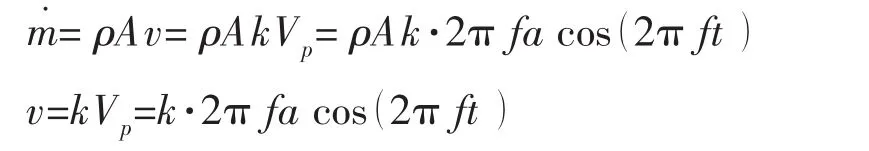
式中：A表示激励器出口面积，k表示活塞面积与激励器出口面积之比，Vp表示活塞的运动速度，a表示活塞振幅。 将代入（6）式，得到：

假设激励器排出的流体可以用一个以激励器出口为底面的圆柱表示，则圆柱高度：

利用（8）式将（7）式简化得到：

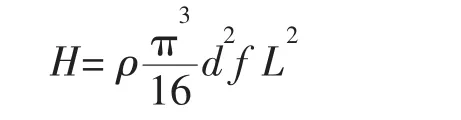
式中：L表示激励器一个行程排出的流体长度，d表示激励器出口直径，f表示激励器活塞振动频率。这样，相同质量流量的稳态射流在一个周期内的平均作用力可表示为：

Krieg和Mohseni[6-7]将（9）式当作合成射流的平均作用力计算公式，通过本文的分析可知，该作用力为相同质量流量下稳态射流的作用力，合成射流的平均作用力比此值偏高。

4 结果及分析

4.1 数据分析

为了研究激励器作用力随出口偏转角度的变化关系，数值计算过程中对激励器受到的流体作用力进行监测，其计算公式为：

式中为激励器表面压强应力矩阵，∂V表示激励器内表面。图8给出激励器不同出口偏角条件下X方向、Y方向作用力变化曲线，其中，X、Y方向定义如图6所示。

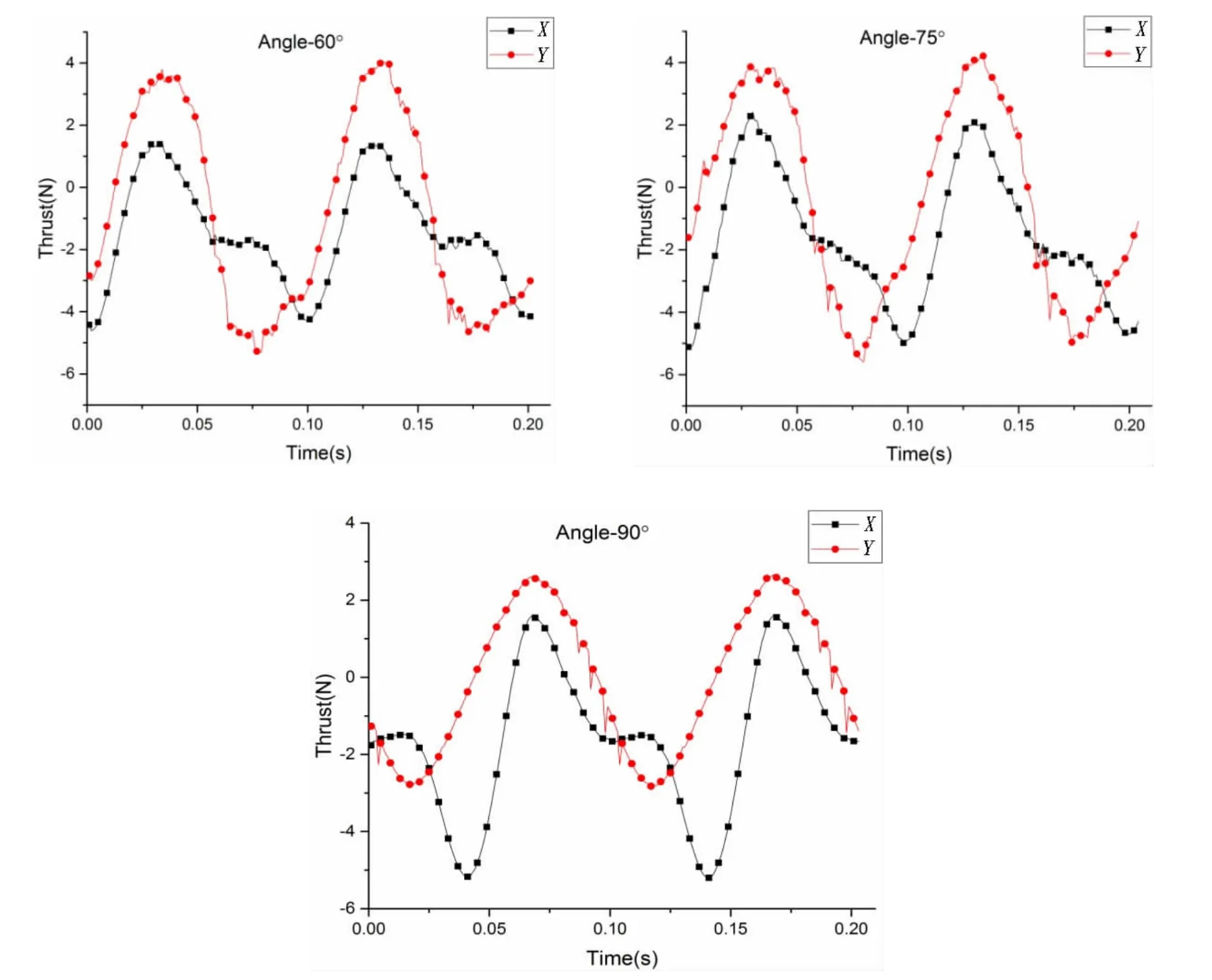
图8 不同偏角条件下X方向、Y方向推力变化曲线Fig.8 The variation of propulsion forces in X direction and Y direction

激励器平均作用力计算公式为：

式中：Fi表示每个时间步作用力数值，由（10）式计算，△t表示时间步长，T表示激励器震动周期，n表示一个周期的时间步数。表3给出了不同偏角条件下激励器X、Y方向的平均作用力。

表3 各偏角所对应的X、Y方向平均作用力Tab.3 The average propulsion force of different cases

从图8可以看出，当激励器出口偏角为0时，X方向的推力很小，且呈现出无规律分布，可以忽略。随着激励器出口偏角的增大，X方向的作用力开始呈现出规律性变化，且作用力幅值逐渐增加。另外，随着出口偏角的增大，作用力曲线出现明显的沿Y轴负向平移现象，且偏角越大，由这种平移所引发的曲线不对称程度越大。作用力曲线不对称说明激励器在一个周期的净平均作用力不为0，曲线的不对称程度越大，净平均作用力越大。因此，从图8可知，随着激励器偏角的增加，激励器X方向的平均作用力逐渐增加，这一点也可以从表3看出。

从图8还可以看出，随着出口偏角的增加，Y方向上的作用力曲线有沿Y轴正向平移的趋势，导致曲线的不对称程度逐渐降低，当偏角增加到90度时，作用力曲线接近对称。可知，随着激励器偏角的增加，Y方向上的净平均作用力逐渐减小，这一点也可从表3看出。

此外，对比图8中X、Y方向推力，当激励器偏角为0时，X方向的作用力幅值很小，基本可以忽略。而当激励器偏角为90度时，Y方向的作用力却仍然具有一定的幅值，并没有完全减小为0。

表3给出了出口不同偏角条件下激励器总作用力，可见总的作用力有一定波动，考虑数值误差的影响，以1.76 N为基准值，可知总的作用力的波动幅值为0.13 N，约占0.13/1.76=7%，波动幅度较小，可以认为在激励器偏角变化过程中，激励器的总作用力保持不变。因此，激励器出口改变后，X、Y方向的作用力求解公式为：

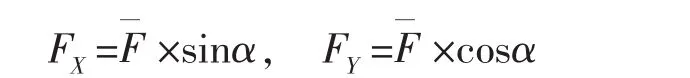
合成射流相对于稳态射流具有推力增强效应[2-3]，为了研究偏角变化对激励器推进效率的影响，本文将不同偏角条件下激励器X、Y方向的作用力与具有相同质量流量的稳态射流作用力进行对比，定义推力增强因子为：

式中表示相同流量条件下稳态射流的平均作用力，由（9）式计算表示合成射流激励器作用力的平均值，由（11）式计算。表4给出了不同偏角条件下X、Y方向的推力以及激励器总推力的增强因子变化。可见，最大推力增强因子达1.55，说明合成射流激励器的推力比相同质量流量条件下的稳态射流提高约50%。另外，还可以看出，随着激励器出口偏角的增加，X方向的推力增强因子逐渐增加，而Y方向的推力增强因子逐渐减小。

表4 不同偏角推力增强因子Tab.4 The scaling factor of propulsion force of different cases

4.2 机理阐释

通过前面的分析可知，合成射流激励器作用力曲线存在关于纵轴的不对称现象，且合成射流推力相对于稳态射流提高约50%，激励器作用力的这种性质可以通过本文建立的数学模型进行解释。

4.2.1 推力增强机理

由激励器作用力模型（5）可知，激励器的作用力主要包括三部分：内部流体加减速所产生的作用力分量、内部流体质量动量变化所产生的作用力分量以及激励器外部流体对控制体的作用力分量，激励器作用力曲线的不对称主要是由激励器外部流体作用力所引起的。

当激励器喷出流体时，激励器外部流体处于相对静止状态，此时激励器喷出的射流相对于外部静止流体具有较大的相对速度，因此，喷射流体会受到外部流体的阻滞作用，将此喷射流体柱视为刚性则其受力如图9，可以看出，外部流体对控制体的作用力方向与激励器对控制体的力的方向相反，因此有

当流体流入激励器时，激励器内部的速度矢量如图10所示，可以看出激励器吸入流体速度相对于激励器内部流体具有一定的相对速度，因此，吸入流体会受到激励器内部流体的阻滞作用，将吸入流体柱视为刚性，则其受力如图10，可以看出，外部流体对于控制体流体的作用力的方向与激励器对控制体的作用力同向，因此有

通过上面的分析可知，当激励器喷出流体时，激励器受到的作用力比基准值偏大，而当激励器吸入流体时，激励器受到的作用力在数值上比基准值偏小，因而激励器作用力曲线整体上有一个沿Y轴平移的趋势。正是外部流体对控制体内流体的这种阻滞作用，使得激励器在质量变化为0的情况下，仍可以产生净作用力。

Krueger通过实验发现合成射流激励器出口存在压强升高现象，是这种阻滞作用力的一种表现，这种现象在稳态射流中并不存在[1]。因而，合成射流相对于稳态射流的推力增强效应来源于外部流体的阻滞作用。

外部流体对喷射流体柱的作用力是由于喷射流体速度较高，而外部流体可看作静止，因此，喷射流体会受到外部流体的阻滞作用。外部流体受激励器活塞激励频率及振幅影响较大，欲利用合成射流的推力增强效应就必须保持外部流体的相对静止状态，因而必须限制激励频率及振幅的大小[6-7，12]。

图9 激励器喷出流体时受力图Fig.9 Force analysis of the ejection process

图10 激励器吸入流体时受力图Fig.10 Force analysis of the injection process

4.2.2 推力随偏角变化机理

由表4可知，随着激励器出口的偏转，X方向的推力增强因子逐渐增强，而Y方向的推力增强因子逐渐减小，这主要是因为当激励器偏角很小时，此时射流方向为Y轴方向，因此，此时推力增强效应主要集中在Y方向。随着激励器偏角的增加，射流逐渐向着X方向偏转，因而外流场的阻滞作用力，即（5）式中的逐渐向X方向偏转，因而X方向的推力增强效应逐渐显著，而Y方向的推力增强效应逐渐丧失。

从图8可以看出，当激励器出口偏角变为90度时，Y方向的作用力仍具有一定幅值，并没有像偏角为0时X方向的作用力那样变为可以忽略的小量，且其平均作用力也并不为0。这是因为激励器作用力主要包括三部分：质量变化引起的作用力分量，流体加减速所引起的作用力分量，以及外部流体对激励期内流体的作用力分量。当激励器偏角为90度时，激励器内部流体的加减速方向仍然为Y方向，因而Y方向的作用力仍具有一定幅值。由于本文所采用的激励函数为对称型，因而，此时Y方向的作用力曲线关于Y轴对称。

另外，由表4知，不同偏转角度下，激励器总的作用力基本保持不变，这说明，合成射流的推力增强效应主要是由外部流体对激励器内部流体的作用力导致的，而且主要集中于激励器喷出流体过程，激励器内流体加减速对激励器的推力增强效应所起的作用较小。

5 结 论

本文设计了一种矢量合成射流激励器，通过数值计算方法分析了激励器作用力随出口偏角的变化关系，建立了合成射流作用力的数学模型，该模型可以很好地解释合成射流作用力的性质，通过本文的分析可知：

（1）合成射流相对于稳态射流推力可提高50%，且通过本文建立的数学模型可知，这种推力增强效应主要是由激励器喷出射流过程中外部流体的阻滞作用引起的。

（2）矢量合成射流激励器总的作用力在出口偏角变化情况下基本保持不变。

（3）矢量合成射流激励器的推力增强效应出现在激励器射流方向。

[1]Krueger PS.The significance of vortex ring formation and nozzle exit over-pressure to pulsatile jet propulsion[D].Sacramento,USA:California Institute of Technology,2001.

[2]Ruiz1 L A,Whittlesey R W,Dabiri JO.Vortex-enhanced propulsion[J].JFluid Mech.,2011,668:5-32.

[3]Krueger PS,Gharib M.Thrust augmentation and vortex ring evolution in a fully pulsed jet[J].AIAA Journal,2005,43(4):792-801.

[4]Glezer A,Amitay M.Synthetic jets[J].Annu.Rev.Fluid Mech.,2002,34:503-529.

[5]Smith B L,Glezer A.Jet vectoring using synthetic jets[J].JFluid Mech.,2002,458:1-34.

[6]Krieg M,Mohseni K.Thrust characterization of a bio-inspired vortex ring thruster for locomotion of underwater robots[J].IEEEJournal of Oceanic Engineering,2008,33(2):123-132.

[7]Krieg M,Mohseni K.Dynamic modeling and control of biologically inspired vortex ring thrusters for underwater robot locomotion[J].IEEETransactions on Robotics,2010.

[8]Li Shuo.A numerical study of micro synthetic jet and its applications in thermal management[D].Atlanta,USA:Georgia Institute of Technology,2005.

[9]Thomas A M,Abraham J P.Numerical simulation of circular synthetic jets with asymmetric forcing profiles[J].The Open Mechanical Engineering Journal,2010,4:1-7.

[10]Kumar A,Panda PK,Kumar V,et al.Combined experimental and numerical study of synthetic jet in quiescent flow[C].Proceedings of the 37th International&4th National Conference on Fluid Mechanics and Fluid Power,2010:1-11.

[11]Thomas A P.Exploration into the feasibility of underwater synthetic jet propulsion[D].Sacramento,USA:California Institute of Technology,2007.

[12]Whittlesey R W,Dabiri JO.Optimal vortex formation in a self-propelled vehicle[J].JFluid Mech.,2013,737:78104.

[13]Krueger PS,Moslemi A A,Nichols JT,et al.Vortex rings in bio-inspired and biological jet propulsion[J].Advances in Science and Technology,2008,58:237-246.

[14]Krieg M,Mohseni K.Modelling circulation,impulse and kinetic energy of starting jets with non-zero radial velocity[J].J Fluid Mech.,2013,719:488526.

[15]Thomas A P,Milano M,G’Sell M G,et al.Synthetic jet propulsion for small underwater vehicles[C].Proceedings of the 2005 IEEE International Conference on Robotics and Automation,2005:181-187.

[16]Dandois J,Garnier E,Sagaut A.Numerical simulation of active separation control by a synthetic jet[J].J Fluid Mech.,2007,574:25-58.

[17]Mohseni K,Gharib M.A model for universal time scale of vortex ring formation[J].Physics of Fluids,1998,10(10):2436-2438.

[18]Rizzetta D P,Visbal M R,Stanek M J.Numerical investigation of synthetic-jet flowfields[J].AIAA Journal,1999,37(8):919-927.