浅谈分类讨论思想在中考数学解题中的应用——以江西省中考数学为例

（江西省赣州市章贡区滨江第一小学 江西赣州 341000）

全日制义务教育数学课程标准要求，“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学基本思想”。分类讨论作为最基本的数学思想方法之一，在中考解题中占有重要的地位。本文主要是以江西省近年的中考试题为例对分类讨论思想进行分析，为教师的有效教学和学生的发散思维提供参考。

一、分类讨论思想

分类讨论是指当问题所给的对象不能进行统一研究时，需要对研究对象按某个标准进行分类，然后逐类讨论，最后综合各类结果得到整个问题的答案。像这种先分类再讨论，把问题“分而治之，各个击破”的解决问题的思想就是分类讨论思想。分类讨论思想能有效地帮助学生整理解题思路，提高解题能力。

应用分类讨论＂化整为零，各个击破，再集零为整＂的数学策略时必须得明确分类原则。

（1）完备性原则 在解题要明确所讨论的问题的全域。

（2）不漏原则 分类必须完整，不能遗漏。

（3）不重复原则 所有的分类之间必须是互斥的。

二、分类讨论思想在初中数学解题中的应用

1.与函数有关问题的应用

函数是数学中非常重要的模块，其中二次函数是中考重点考察的内容，通过对近年中考题的分析发现，有关二次函数的考题多涉及参数，学生用分类讨论思想能很好地解决这一类问题。

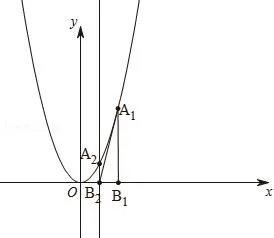
例：（2016·江西）设抛物线的解析式为y=ax2，过点B1（1，0）作x轴的垂线，交抛物线于点A1（1，2）；过点作x轴的垂线，交抛物线于点A2；…；过点（n为正整数）作x轴的垂线，交抛物线于点An，连接AnBn+1，得Rt△AnBnBn+1。

2.在系列Rt△AnBnBn+1中，探究下列问题：

①当n为何值时，Rt△AnBnBn+1是等腰直角三角形？

② 设1≤k＜m≤n（k，m均为正整数），问： 是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似？若存在，求出其相似比；若不存在，说明理由.

【分析】因为Rt△AkBkBk+1与Rt△AmBmBm+1是直角三角形，所以分两种情况讨论：根据结论代入所得的对应边的比列式，计算求出k与m的关系，并与1≤k＜m≤n（k，m均为正整数）相结合，得出两种符合条件的值，分别代入两相似直角三角形计算相似比.

【解答】由Rt△AnBnBn+1是等腰直角三角形得AnBn=BnBn+1，

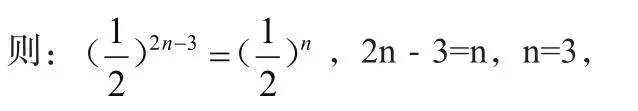
∴当n=3时，Rt△AnBnBn+1是等腰直角三角形，

②依题意得，∠AkBkBk+1=∠AmBmBm+1=90°，

有两种情况：i）当Rt△AkBkBk+1∽Rt△AmBmBm+1时，

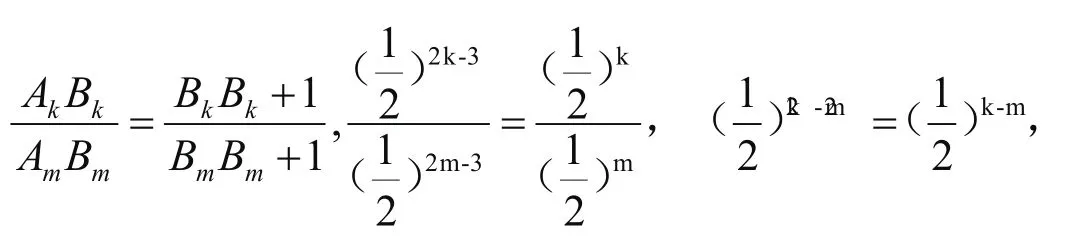
所以，k=m（舍去），

ii）当Rt△AkBkBk+1∽Rt△Bm+1BmAm时，

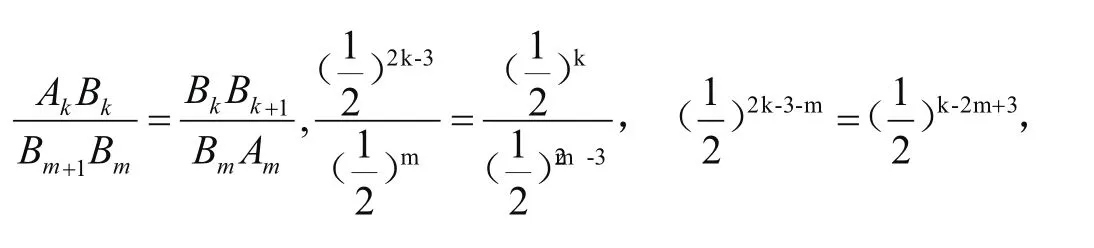
∴k+m=6，

∵1≤k＜m≤n（k，m均为正整数），

∴取或

当时，Rt△A1B1B2∽Rt△B6B5A5，

相似比为：

当时，Rt△A2B2B3∽Rt△B5B4A4，

相似比为：

所以：存在Rt△AkBkBk+1与Rt△AmBmBm+1相似，其相似比为64：1或8：1.